Abstract
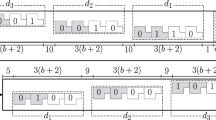
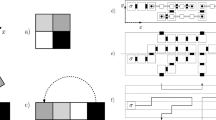
In this paper, we study the minimum number of unique tile types required for the self-assembly of thin rectangles in Winfree’s abstract Tile Assembly Model (aTAM), restricted to temperature-1. Using Catalan numbers, planar self-assembly and a restricted version of the Window Movie Lemma, we derive a new lower bound on the tile complexity of thin rectangles at temperature-1 in 2D. Then, we give the first known upper bound on the tile complexity of “just-barely” 3D thin rectangles at temperature-1, where tiles are allowed to be placed at most one step into the third dimension. Our construction, which produces a unique terminal assembly, implements a just-barely 3D, zig-zag counter, whose base depends on the dimensions of the target rectangle, and whose digits are encoded geometrically, vertically-oriented and in binary.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
Notes
- 1.
A cut-set is a subset of edges in a graph which, when removed from the graph, produces two or more disconnected subgraphs. The weight of a cut-set is the sum of the weights of all of the edges in the cut-set.
References
Adleman, L.M., Cheng, Q., Goel, A., Huang, M.-D.: Running time and program size for self-assembled squares. In: STOC, pp. 740–748 (2001)
Aggarwal, G., Cheng, Q., Goldwasser, M.H., Kao, M.-Y., de Espanés, P.M., Schweller, R.T.: Complexities for generalized models of self-assembly. SIAM J. Comput. 34, 1493–1515 (2005)
Barish, R.D., Schulman, R., Rothemund, P.W., Winfree, E.: An information-bearing seed for nucleating algorithmic self-assembly. Proc. Nat. Acad. Sci. 106(15), 6054–6059 (2009)
Cook, M., Fu, Y., Schweller, R.: Temperature 1 self-assembly: deterministic assembly in 3D and probabilistic assembly in 2D. In: Proceedings of the 22nd Annual ACM-SIAM Symposium on Discrete Algorithms (2011)
Doty, D., Patitz, M.J., Summers, S.M.: Limitations of self-assembly at temperature 1. Theor. Comput. Sci. 412, 145–158 (2011)
Furcy, D., Micka, S., Summers, S.M.: Optimal program-size complexity for self-assembled squares at temperature 1 in 3D. Algorithmica 77(4), 1240–1282 (2017)
Furcy, D., Summers, S.M.: Optimal self-assembly of finite shapes at temperature 1 in 3D. Algorithmica 80(6), 1909–1963 (2018)
Manuch, J., Stacho, L., Stoll, C.: Two lower bounds for self-assemblies at temperature 1. J. Comput. Biol. 17(6), 841–852 (2010)
Mao, C., LaBean, T.H., Relf, J.H., Seeman, N.C.: Logical computation using algorithmic self-assembly of DNA triple-crossover molecules. Nature 407(6803), 493–496 (2000)
Meunier, P.-E., Patitz, M.J., Summers, S.M., Theyssier, G., Winslow, A., Woods, D.: Intrinsic universality in tile self-assembly requires cooperation. In: Proceedings of the 25th Annual ACM-SIAM Symposium on Discrete Algorithms (SODA), pp. pp. 752–771 (2014)
Meunier, P.-É., Woods, D.: The non-cooperative tile assembly model is not intrinsically universal or capable of bounded turing machine simulation. In: Proceedings of the 49th Annual ACM SIGACT Symposium on Theory of Computing, STOC 2017, Montreal, 19–23 June 2017, pp. 328–341 (2017)
Rothemund, P.W.K., Winfree, E.: The program-size complexity of self-assembled squares (extended abstract). In: STOC 2000: Proceedings of the Thirty-Second Annual ACM Symposium on Theory of Computing, pp. 459–468 (2000)
Rothemund, P.W.K., Papadakis, N., Winfree, E.: Algorithmic self-assembly of DNA Sierpinski triangles. PLoS Biol. 2(12), 2041–2053 (2004)
Schulman, R., Winfree, E.: Synthesis of crystals with a programmable kinetic barrier to nucleation. Proc. Nat. Acad. Sci. 104(39), 15236–15241 (2007)
Seeman, N.C.: Nucleic-acid junctions and lattices. J. Theor. Biol. 99, 237–247 (1982)
Soloveichik, D., Winfree, E.: Complexity of self-assembled shapes. SIAM J. Comput. 36(6), 1544–1569 (2007)
Winfree, E.: Algorithmic self-assembly of DNA. Ph.D. thesis, California Institute of Technology, June 1998
Winfree, E., Liu, F., Wenzler, L.A., Seeman, N.C.: Design and self-assembly of two-dimensional DNA crystals. Nature 394(6693), 539–544 (1998)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this paper
Cite this paper
Furcy, D., Summers, S.M., Wendlandt, C. (2019). New Bounds on the Tile Complexity of Thin Rectangles at Temperature-1. In: Thachuk, C., Liu, Y. (eds) DNA Computing and Molecular Programming. DNA 2019. Lecture Notes in Computer Science(), vol 11648. Springer, Cham. https://doi.org/10.1007/978-3-030-26807-7_6
Download citation
DOI: https://doi.org/10.1007/978-3-030-26807-7_6
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-26806-0
Online ISBN: 978-3-030-26807-7
eBook Packages: Computer ScienceComputer Science (R0)