Abstract
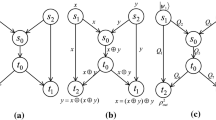
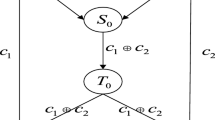
How to establish a secure and efficient quantum network coding algorithm is one of important research topics of quantum secure communications. Based on the butterfly network model and the characteristics of easy preparation of Bell states, a novel anti-noise quantum network coding protocol is proposed in this paper. The new protocol encodes and transmits classical information by virtue of Bell states. It can guarantee the transparency of the intermediate nodes during information, so that the eavesdropper Eve disables to get any information even if he intercepts the transmitted quantum states. In view of the inevitability of quantum noise in quantum channel used, this paper analyzes the influence of four kinds of noises on the new protocol in detail further, and verifies the efficiency of the protocol under different noise by mathematical calculation and analysis. In addition, based on the detailed mathematical analysis, the protocol has functioned well not only on improving the efficiency of information transmission, throughput and link utilization in the quantum network, but also on enhancing reliability and anti-eavesdropping attacks.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
References
Yu, S.L., Pan, J.W.: I have a quantum dream in mind. The People’s Daily, 04 June 2014
Qu, Z.G., Zhu, T.C., Wang, J.W., Wang, X.J.: A novel quantum stegonagraphy based on brown states. Comput. Mater. Continua 56(1), 47–59 (2018)
Liu, W.J., Chen, Z.Y., Liu, J.S., Su, Z.F., Chi, L.H.: Full-blind delegating private quantum computation. Comput. Mater. Continua 56(2), 211–223 (2018)
Bennett, C.H.: Quantum cryptography using any two nonorthogonal states. Phys. Rev. Lett. 68(21), 3121 (1992)
Bennett, C.H., Brassard, G.: Quantum cryptography: public key distribution and coin tossing. In: Proceedings of IEEE International Conference on Computers Systems and Signal Processing, vol. 175, pp. 175–179 (1984)
Hayashi, M.: Prior entanglement between senders enables perfect quantum network coding with modification. Phys. Rev. A 76(4), 538 (2007)
Hayashi, M., Iwama, K., Nishimura, H., Raymond, R., Yamashita, S.: Quantum network coding. In: Thomas, W., Weil, P. (eds.) STACS 2007. LNCS, vol. 4393, pp. 610–621. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-70918-3_52
Shang, T., Zhao, X.J., Wang, C., et al.: Controlled quantum network coding scheme based on single controller. Acta Electronica Sinica 42(10), 1913–1917 (2014)
Bennett, C.H., Brassard, G., Crepeau, C.: Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels. Phys. Rev. Lett. 70(13), 1895–1899 (1993)
Moroder, T., Kleinmann, M., Schindler, P., Monz, T., Gühne, O., Blatt, R.: Certifying systematic errors in quantum experiments. Phys. Rev. Lett. 110(18), 180401 (2012)
Peng, C.Z., Yang, T., Bao, X.H., et al.: Experimental free-space distribution of entangled photon pairs over 13 km: towards satellite-based global quantum communication. Phys. Rev. Lett. 94(15), 150501 (2005)
Yin, J., Ren, J.G., Lu, H., et al.: Quantum teleportation and entanglement distribution over 100-kilometre free-space channels. Nature 488(7410), 185–188 (2013)
Akter, L., Natarajan, B.: QoS constrained resource allocation to secondary users in cognitive radio networks. Comput. Commun. 32(18), 1923–1930 (2009)
Ma, S.Y., Chen, X.B., Luo, M.X.: Probabilistic quantum network coding of M-qudit states over the butterfly network. Opt. Commun. 283(3), 497–501 (2009)
Yan, S.S., Kuang, H.M., Guo, Y.: Quantum coding of butterfly network based on controlled quantum teleportation. National Sci. Paper Online Excellent Paper 5(20), 1996–2001 (2012)
Nishimura, H.: Quantum network coding — How can network coding be applied to quantum information. In: International Symposium on Network Coding, pp. 1–5. IEEE (2013)
Korotkov, A.N., Keane, K.: Decoherence suppression by quantum measurement reversal. Phys. Rev. A 81(81), 1334–1342 (2010)
Guan, X.W., Chen, X.B., Wang, L.C.: Joint remote preparation of an arbitrary two-qubit state in noisy environments. Int. J. Theor. Phys. 53(7), 2236–2245 (2014)
Fortes, R., Rigolin, G.: Fighting noise with noise in realistic quantum teleportation. Phys. Rev. A 92(1), 012338 (2015)
Wang, M.M., Qu, Z.G.: Effect of quantum noise on deterministic joint remote state preparation of a qubit state via a GHZ channel. Quantum Inf. Process. 15(11), 4805–4818 (2016)
Wang, M.M., Qu, Z.G., Wang, W.: Effect of noise on deterministic joint remote preparation of an arbitrary two-qubit state. Quantum Inf. Process. 16(5), 140 (2017). UNSP
Wang, M.M., Qu, Z.G., Wang, W., Chen, J.G.: Effect of noise on joint remote preparation of multi-qubit state. Int. J. Quantum Inf. 15(02), 175–179 (2017)
Yu, W., Cioffi, J.M.: FDMA capacity of Gaussian multiple-access channels with ISI. In: IEEE International Conference on Communications, vol. 50, no. 1, pp. 102–111 (2002)
Iri, M.: On an extension of the maximum flow minimum cut theorem to multicommodity flows. J. Oper. Res. Soc. Japan 13, 129–135 (1971)
Acknowledgments
This work was supported by the National Natural Science Foundation of China (No. 61373131, 61303039, 61772281, 61232016, 61501247), Natural Science Foundation of Jiangsu Province (Grant No. BK20171458), Sichuan Youth Science and Technique Foundation (No. 2017JQ0048), NUIST Research Foundation for Talented Scholars (2015r014), PAPD and CICAEET funds.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this paper
Cite this paper
Qu, Z., Zhang, Z., Cheng, Z. (2019). Anti-noise Quantum Network Coding Protocol Based on Bell States and Butterfly Network Model. In: Sun, X., Pan, Z., Bertino, E. (eds) Artificial Intelligence and Security. ICAIS 2019. Lecture Notes in Computer Science(), vol 11634. Springer, Cham. https://doi.org/10.1007/978-3-030-24271-8_6
Download citation
DOI: https://doi.org/10.1007/978-3-030-24271-8_6
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-24270-1
Online ISBN: 978-3-030-24271-8
eBook Packages: Computer ScienceComputer Science (R0)