A Mathematical Model for Enhancer Activation Kinetics During Cell Differentiation

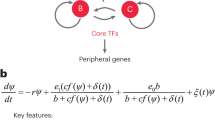
Abstract

Cell differentiation and development are for a great part steered by cell type specific enhancers. Transcription factor (TF) binding to an enhancer together with DNA looping result in transcription initiation. In addition to binding motifs for TFs, enhancer regions typically contain specific histone modifications. This information has been used to detect enhancer regions and classify them into different subgroups. However, it is poorly understood how TF binding and histone modifications are causally connected and what kind of molecular dynamics steer the activation process.

Contrary to previous studies, we do not treat the activation events as static epigenetic marks but consider the enhancer activation as a dynamic process. We develop a mathematical model to describe the dynamic mechanisms between TF binding and histone modifications known to characterize an active enhancer. We estimate model parameters from time-course data and infer the causal relationships between TF binding and different histone modifications. We benchmark the performance of this framework using simulated data and survey the ability of our method to identify the correct model structures for a variety of system dynamics, noise levels and the number of measurement time points.

Appendix

Table 2. The simulated models and the means of the parameters used in data simulations. One representative from each model family were selected for generating data. Index $k \in \{0,1,7,11 \}$ specifies the model structure as described in Table 1. A sampled parameter vector $\varvec{\theta }_k$ consists of kinetic parameters $\theta _{kl}$, initial values for three ordered enhancer activation signals denoted by $x_0$, $y_0$ and $z_0$ and the simulation specific measurement noise $\sigma _s$ which was 0.15, 0.25, 0.5, 0.75, 1, 1.25 1.5 or 2.0. Independent, cascade and synergistic models have six kinetic parameters. Consecutive odd and even elements are the activation rates and the corresponding deactivation rates of the enhancer activation signal, respectively. Additive models have seven kinetic parameters. First four of them are the basal activation and the deactivation rates of enhancer activity signal x and y mediating dynamics independent from other variables while $\theta _{k5}$ and $\theta _{k6}$ are the activation rates of z activation caused by x and y and $\theta _{k7}$ is the deactivation rate of z.