Abstract
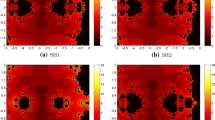
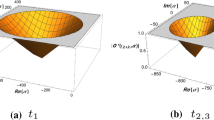
Finding repeated zero for a nonlinear equation \(f(x)=0\), \(f:I\subseteq R\rightarrow R\), has always been of much interest and attention due to it’s wide applications in many fields of science and engineering. The modified Newton’s method is usually applied to solve this problem. Keeping in view that very few optimal higher order convergent methods exist for multiple roots, we present a new family of optimal eighth order convergent iterative methods for multiple roots with known multiplicity involving multivariate weight function. The numerical performance of the proposed methods is analyzed extensively along with the basins of attractions. Real life models from Life Science, Engineering and Physics are considered for the sake of comparison. The numerical experiments show that our proposed methods are efficient for determining multiple roots of non-linear equations.
This is a preview of subscription content, log in via an institution to check access.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
References
Schroder, E.: Uber unendlich viele algorithmen zur auflosung der gleichungen. Math. Ann. 2, 317–365 (1870)
Kung, H.T., Traub, J.F.: Optimal order of one-point and multipoint iteration. J. Assoc. Comput. Mach. 21, 643–651 (1974)
Geum, Y.H., Kim, Y.I., Neta, B.: A class of two-point sixth-order multiple-zero finders of modified double-Newton type and their dynamics. Appl. Math. Comput. 270, 387–400 (2015)
Geum, Y.H., Kim, Y.I., Neta, B.: A sixth-order family of three-point modified Newton-like multiple-root finders and the dynamics behind their extraneous fixed points. Appl. Math. Comput. 283, 120–140 (2016)
Behl, R., Cordero, A., Motsa, S.S., Torregrosa, J.R.: Aneighth-order family of optimal multiple root finders and its dynamics. Numer. Algor. 77(4), 1249–1272 (2017). https://doi.org/10.1007/s11075-017-0361-6
Zafar, F., Cordero, A., Rana, Q., Torregrosa, J.R.: Optimal iterative methods for finding multiple roots of nonlinear equations using free parameters. J. Math. Chem. 56(7), 1884–1901 (2018). https://doi.org/10.1007/s10910-017-0813-1
Behl, R., Zafar, F., Alshomrani, A.S., Junjua, M., Yasmin, N.: An optimal eighth-order scheme for multiple zeros of univariate function. Int. J. Comput. Math. 15(3), 14 (2018). https://doi.org/10.1142/S0219876218430028
Behl, R., Alshomrani, A.S., Motsa, S.S.: An optimal schemefor multiple roots of nonlinear equations with eighth-order convergence. J. Math. Chem. 56(7), 1–6 (2018). https://doi.org/10.1007/s10910-018-0857-x
Jay, L.O.: A note on Q-order of convergence. BIT Numer. Math. 41, 422–429 (2001)
Edelstein-Keshet, L.: Differential Calculus for the Life Sciences. Univeristy of British Columbia, Vancouver (2017)
Zachary, J.L.: Introduction to Scientific Programming: Computational Problem Solving Using Maple and C. Springer, New York (2012)
Khoury, R., Harder, D.H.: Numerical Methods and Modelling for Engineering. Springer, Switzerland (2017)
Acknowledgments
This work is supported by Schlumberger Foundation-Faculty for Future Program, by Ministerio de Economía y Competitividad under grants MTM 2014-52016-C2-2-P and Generalitat Valenciana PROMETEO/2016/089.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this paper
Cite this paper
Zafar, F., Cordero, A., Torregrosa, J.R. (2019). A Family of Optimal Eighth Order Multiple Root Finders with Multivariate Weight Function. In: Dimov, I., Faragó, I., Vulkov, L. (eds) Finite Difference Methods. Theory and Applications. FDM 2018. Lecture Notes in Computer Science(), vol 11386. Springer, Cham. https://doi.org/10.1007/978-3-030-11539-5_78
Download citation
DOI: https://doi.org/10.1007/978-3-030-11539-5_78
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-11538-8
Online ISBN: 978-3-030-11539-5
eBook Packages: Computer ScienceComputer Science (R0)