State of the Art in Shape Matching | SpringerLink
Skip to main content
Springer Nature Link
Log in

State of the Art in Shape Matching

  • Chapter
Principles of Visual Information Retrieval

Part of the book series: Advances in Pattern Recognition ((ACVPR))

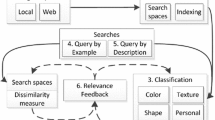
Abstract

Large image databases are used in an extraordinary number of multimedia applications in fields such as entertainment, business, art, engineering, and science. Retrieving images by their content, as opposed to external features, has become an important operation. A fundamental ingredient for content-based image retrieval is the technique used for comparing images. There are two general methods for image comparison: intensity based (color and texture) and geometry based (shape). A recent user survey about cognition aspects of image retrieval shows that users are more interested in retrieval by shape than by color and texture [62]. However, retrieval by shape is still considered one of the most difficult aspects of content-based search. Indeed, systems such as IBM’s Query By Image Content, QBIC [57], perhaps one of the most advanced image retrieval systems to date, is relatively successful in retrieving by color and texture, but performs poorly when searching on shape. A similar behavior is exhibited in the new Alta Vista photo finder [10].

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution

Subscribe and save

Springer+ Basic
¥17,985 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Chapter
JPY 3498
Price includes VAT (Japan)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever
eBook
JPY 11439
Price includes VAT (Japan)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever
Softcover Book
JPY 14299
Price includes VAT (Japan)
  • Compact, lightweight edition
  • Dispatched in 3 to 5 business days
  • Free shipping worldwide - see info
Hardcover Book
JPY 14299
Price includes VAT (Japan)
  • Durable hardcover edition
  • Dispatched in 3 to 5 business days
  • Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Preview

Unable to display preview. Download preview PDF.

Unable to display preview. Download preview PDF.

Similar content being viewed by others

References

  1. Agarwal, PK, Sharir, M, and Toledo, S, “Applications of Parametric Searching in Geometric Optimization”, J Algorith, 17, pp. 292–318, 1994.

    Article  MathSciNet  Google Scholar 

  2. Agarwal, PK, Efrat, A, and Sharir, M, “Vertical Decomposition of Shallow Levels in 3-Dimensional Arrangements and its Applications”, 11th Annual ACM Symposium on Computational Geometry, pp. 39-50, 1995.

    Google Scholar 

  3. Aichholzer, O, Alt, H, and Rote, G, “Matching Shapes with a Reference Point”, Int J Comput Geometry and Applic, 7, pp. 349–363, August, 1997.

    Article  MathSciNet  MATH  Google Scholar 

  4. Alt, H, Mehlhorn, K, Wagener, H, and Welzl, E, “Congruence, Similarity, and Symmetries of Geometric Objects”, Discrete Comput Geometry, 3, pp. 237–256, 1988.

    Article  MathSciNet  MATH  Google Scholar 

  5. Alt, H, Blömer, J, Godau, G, and Wagener, H, “Approximation of Convex Polygons”, 17th International Colloquium on Automata, Languages, and Programming (ICALP), Lecture Notes in Computer Science 443, pp. 703-716, Springer, 1990.

    Google Scholar 

  6. Alt, H, Behrends, B, and Blömer, J, “Approximate Matching of Polygonal Shapes”, 7th Annual ACM Symposium on Computational Geometry, pp. 186-193, 1992.

    Google Scholar 

  7. Alt, H, Behrends, B, and Blömer, J, “Approximate Matching of Polygonal Shapes”, Ann Math Artif Intell, pp. 251-265, 1995.

    Google Scholar 

  8. Alt, H and Godeau, M, “Computing the Préchet Distance Between Two Polygonal Curves”, Int J Comput Geometry & Applic, pp. 75-91, 1995.

    Google Scholar 

  9. Alt, H, Fuchs, U, Rote, G, and Weber, G, “Matching Convex Shapes with Respect to the Symmetric Difference”, Algorithms ESA’ 96, 4th Annual European Symposium on Algorithms, Barcelona, Spain, pp. 320-333, September 1996. Lecture Notes in Computer Science 1136, Springer, 1996.

    Google Scholar 

  10. Alta Vista Photo Finder, http://image.altavista.com/cgi-bin/avncgi.

    Google Scholar 

  11. Amenta, N, “Computational Geometry Software”, In Goodman and O’Rourke [32], chapter 52, pp. 951–960, 1997.

    MathSciNet  Google Scholar 

  12. Arkin, E, Chew, P, Huttenlocher, D, Kedem, K, and Mitchel, J, “An Efficiently Computable Metric for Comparing Polygonal Shapes”, IEEE Trans Patt Anal Mach Intell, 13(3), pp. 209–215, 1991.

    Article  Google Scholar 

  13. Arya, S, Mount, DM, Netanyahu, NS, Silverman, R, and Wu, A, “An Optimal Algorithm for Approximate Nearest Neighbor Searching”, 5th Annual ACM-SIAM Symposium on Discrete Algorithms, pp. 573-582, 1994.

    Google Scholar 

  14. Ballard, DH, “Generalized Hough Transform to Detect Arbitrary Patterns”, IEEE Trans Patt Anal Mach Intell, 13(2), pp. 111–122, 1981.

    MATH  Google Scholar 

  15. Ballard, DH and Brown, CM, Computer Vision, Prentice Hall, 1982.

    Google Scholar 

  16. Boissonnat, JD and Yvinec, M, Algorithmic Geometry, Cambridge University Press, 1998.

    Google Scholar 

  17. Borgefors, G, “Distance Transforms in Digital Images”, Computer Vision Graphics Image Process, 34, pp. 344–371, 1986.

    Article  Google Scholar 

  18. Borgefors, G, “Hierarchical Chamfer Matching: a Parametric Edge Matching Algorithm”, IEEE Trans Patt Anal Mach Intell, 10(6), pp. 849–865, November 1988.

    Article  Google Scholar 

  19. Brass, P and Knauer, C, “Testing the Congruence of d-Dimensional Point Sets”, 16th Annual Symposium on Computational Geometry, 2000.

    Google Scholar 

  20. Chen, CC, “Improved Moment Invariants for Shape Discrimination”, Patt Recogn, 26(5), pp. 683–686, 1993.

    Article  Google Scholar 

  21. Chew, P and Kedem, K, “Improvements on Approximate Pattern Matching”, 3rd Scandinavian Workshop on Algorithm Theory, Lecture Notes in Computer Science 621, pp. 318–325. Springer, 1992.

    Article  MathSciNet  Google Scholar 

  22. Chew, LP, Goodrich, MT, Huttenlocher, DP, Kedem, K, Kleinberg, JM, and Kravet, D, “Geometric Pattern Matching Under Euclidean Motion”, Comput Geometry Theory and Applic, 7, pp. 113–124, 1997.

    Article  MATH  Google Scholar 

  23. Chin, F, Snoeyink, J, and Wang, CA, “Finding the Medial Axis of a Simple Polygon in Linear Time”, 6th Annual International Symposium on Algorithms Computation (ISAAC 95), Lecture Notes in Computer Science 1004, pp. 382–391. Springer, 1995.

    Article  MathSciNet  Google Scholar 

  24. Cohen, SD and Guibas, LJ, “Partial Matching of Planar Polylines Under Similarity Transformations”, 8th Annual Symposium on Discrete Algorithms, pp. 777-786, 1997.

    Google Scholar 

  25. Copson, ET, Metric Spaces, Cambridge University Press, 1968.

    Google Scholar 

  26. de Berg, M, Devillers, O, van Kreveld, M, Schwarzkopf, O, and Teillaud, M, “Computing the Maximum Overlap of Two Convex Polygons Under Translation”, 7th Annu. Internat. Sympos. Algorithms Comput, 1996.

    Google Scholar 

  27. de Berg, M, van Kreveld, M, Overmars, M, and Schwarzkopf, O, Computational Geometry: Algorithms and Applications, Springer-Verlag, 1997.

    Google Scholar 

  28. Efrat, A and Itai, A, “Improvements on Bottleneck Matching and Related Problems Using Geometry”, 12th Symposium on Computational Geometry, pp. 301-310, 1996.

    Google Scholar 

  29. Efrat, A and Katz, MJ, “Computing Fair and Bottleneck Matchings in Geometric Graphs”, 7th International Symposium on Algorithms and Computation, pp. 115-125, 1996.

    Google Scholar 

  30. Godau, M, “A Natural Metric for Curves-Computing the Distance for Polygonal Chains and Approximation Algorithms”, Symposium on Theoretical Aspects of Computer Science (STACS), Lecture Notes in Computer Science 480, pp. 127–136, Springer, 1991.

    Article  MathSciNet  Google Scholar 

  31. Gold, S, Matching and Learning Structural and Spatial Representations with Neural Networks, PhD thesis, Yale University, 1995.

    Google Scholar 

  32. Goodman, JE and O’Rourke, J, editors, Handbook of Discrete and Computational Geometry, CRC Press, 1997.

    Google Scholar 

  33. Günsel, B and Tekalp, M, “Shape Similarity Matching for Query-by-Example”, Patt Recogn, 31(7), pp. 931–944, 1998.

    Article  Google Scholar 

  34. Hagedoorn, M and Veitkamp, RC, “Metric Pattern Spaces”, Technical Report UU-CS-1999-03, Utrecht University, 1999.

    Google Scholar 

  35. Hagedoorn, M and Veitkamp, RC, “Reliable and Efficient Pattern Matching Using an Affine Invariant Metric”, Int J Computer Vision, 31(2/3), pp. 203–225, 1999.

    Article  Google Scholar 

  36. Hagedoorn, M and Veltkamp, RC, “A Robust Affine Invariant Metric on Boundary Patterns”, Int J Pattern Recogn Patt Anal, 13(8), pp. 1151–1164, December, 1999.

    Article  Google Scholar 

  37. Huttenlocher, D and Ullman, S, “Object Recognition Using Alignment”, International Conference on Computer Vision, London, pp. 102-111, 1987.

    Google Scholar 

  38. Huttenlocher, DP and Kedem, K, “Computing the Minimum Hausdorff Distance for Point Sets Under Translation”, Proc. 6th Annual ACM Symp. Computational Geometry, pp. 340-349, 1990.

    Google Scholar 

  39. Huttenlocher, DP, Kedem, K, and Kleinberg, JM, “On Dynamic Voronoi Diagrams and the Minimum Hausdorff Distance for Point Sets Under Euclidean Motion in the Plane”, 8th Annuual ACM Symposium on Computational Geometry, pp. 110-120, 1992.

    Google Scholar 

  40. Huttenlocher, DP, Klanderman, GA, and Rucklidge, WJ, “Comparing Images Using the Hausdorff Distance”, IEEE Trans Patt Anal Mach Intell, 15, pp. 850–863, 1993.

    Article  Google Scholar 

  41. Huttenlocher, DP, Kedem, K, and Sharir, M, “The Upper Envelope of Voronoi Surfaces and its Applications”, Discrete Comput Geometry, 9, pp. 267–291, 1993.

    Article  MathSciNet  MATH  Google Scholar 

  42. Imai, H and Iri, M, “Polygonal Approximation of a Curve-Formulations and Algorithms”, in Toussaint [69], pp. 71–86, 1988.

    MathSciNet  Google Scholar 

  43. Jacobs, C, Finkelstein, A, and Salesin, D, “Fast Multiresolution Image Querying”, Computer Graphics Proceedings SIGGRAPH, pp. 277-286, 1995.

    Google Scholar 

  44. Khotanzad, A and Hong, YH, “Invariant Image Recognition by Zernike Moments”, IEEE Trans Patt Anal Mach Intell, 12(5), pp. 489–497, 1990.

    Article  Google Scholar 

  45. Kruskal, JB, “An Overview of Sequence Comparison: Time Warps, String Edits, and Macromolecules”, SIAM Rev, 25, pp. 201–237, 1983.

    Article  MathSciNet  MATH  Google Scholar 

  46. Lamdan, Y and Wolfson, H J, “Geometric Hashing: a General and Efficient Model-Based Recognition Scheme”, 2nd International Conference on Computer Vision, pp. 238-249, 1988.

    Google Scholar 

  47. Latecki, LJ and Lakämper, R, “Convexity Rule for Shape Decomposition Based on Discrete Contour Evolution”, Computer Vision Image Understand, 73(3), pp. 441–454, 1999.

    Article  Google Scholar 

  48. Loncaric, S, “A Survey of Shape Analysis Techniques”, Patt Recogn, 31(8), pp. 983–1001, 1998.

    Article  Google Scholar 

  49. Mokhtarian, F, Abbasi, S, and Kitt1er, J, “Efficient and Robust Retrieval by Shape Content Through Curvature Scale Space” Image Databases and Multi-Media Search, First International Workshop IDB-MMS’96, Amsterdam, The Netherlands, pp. 35-42, 1996.

    Google Scholar 

  50. Mount, DM and Wu, AY, “On the Area of Overlap of Translated Polygons”, Comput Vision Image Understand, 64, pp. 53–61, July, 1996.

    Article  Google Scholar 

  51. Mulmuley, K, Computational Geometry: An Introduction Through Randomized Algorithms, Prentice Hall, 1993.

    Google Scholar 

  52. Niblack, W, Barber, R, Equitz, W, Flickner, M, Glasman, E, Petkovic, D, Yanker, P, Faloutsos, C, and Taubin, G, “The QBIC project: Querying Image by Content Using Color, Texture, and Shape”, Electronic Imaging: Storage and Retrieval for Image and Video Databases, Proceedings SPIE, 1908, pp. 173–187, 1993.

    Article  Google Scholar 

  53. Olson, CF, “Efficient Pose Clustering Using a Randomized Algorithm”, Int J Computer Vision, 23(2), pp. 131–147, 1997.

    Article  Google Scholar 

  54. O’Rourke, J, “Curve Similarity via Signatures”, in Toussaint [69], pp. 295–317, 1985.

    Google Scholar 

  55. O’Rourke, J, Computational Geometry in C, Cambridge University Press, 1994.

    Google Scholar 

  56. Prokop, RJ and Reeves, AP, “A Survey of Moment-Based Techniques for Unoccluded Object Representation and Recognition”, CVGIP: Graphics Models Image Process, 54(5), pp. 438–460, 1992.

    Article  Google Scholar 

  57. QBIC project, http://wwwqbic.almaden.ibm.com/.

    Google Scholar 

  58. Ranade, S and Rosenfeld, A, “Point Pattern Matching by Relaxation”, Patt Recogn, 12, pp. 269–275, 1980.

    Article  Google Scholar 

  59. Rosin, PL, “Techniques for Assessing Polygonal Approximations of Curves”, IEEE Trans Patt Recogn Mach Intell, 19(5), pp. 659–666, 1997.

    Article  Google Scholar 

  60. Rucklidge, W, Efficient Visual Recognition Using the Hausdorff Distance, Lecture Notes in Computer Science, Springer, 1996.

    Google Scholar 

  61. Schirra, S, “Approximate Decision Algorithms for Approximate Congruence”, Inform Process Lett, 43, pp. 29–34, 1992.

    Article  MathSciNet  MATH  Google Scholar 

  62. Schomaker, L, de Leau, E, and Vuurpijl, L, “Using Pen-Based Outlines for Object-Based Annotation and Image-Based Queries”, Visual Information and Information Systems — Third International Conference VISUAL’99, Amsterdam, The Netherlands, Lecture Notes in Computer Science 1614, pp. 585-592, June, 1999.

    Google Scholar 

  63. Schwerdt, J, Smid, M, and Schirra, S, “Computing the Minimum Diameter for Moving Points: An Exact Implementation Using Parametric Search”, 13th Annual ACM Symposium on Computational Geometry, pp. 466-468, 1997.

    Google Scholar 

  64. Sclaroff, S and Pentland, AP, “Modal Matching for Correspondence and Recognition”, IEEE Trans Patt Anal Mach Intell, 17(6), pp. 545–561, 1995.

    Article  Google Scholar 

  65. Sclaroff, S, “Deformable Prototypes for Encoding Shape Categories in Image Databases”, Patt Recogn, 30(4), pp. 627–641, 1997.

    Article  Google Scholar 

  66. Small, CG, The Statistical Theory of Shapes, Springer Series in Statistics, Springer, 1996.

    Google Scholar 

  67. Steger, C, “On the Calculation of Arbitrary Moments of Polygons”, Technical Report, Dept. Computer Science, University of München, October, 1996.

    Google Scholar 

  68. Stockman, G, “Object Recognition and Localization via Pose Clustering”, Computer Vision Graphics Image Process, 40(3), pp. 361–387, 1987.

    Article  Google Scholar 

  69. Toussaint, GT editor, Computational Morphology, North-Holland, 1988.

    Google Scholar 

  70. Ullman, S, High-Level Vision, MIT Press, 1996.

    Google Scholar 

  71. Umeyama, S, “Parameterized Point Pattern Matching and its Application to Recognition of Object Families”, IEEE Trans Patt Anal and Mach Intell, 15(1), pp. 136–144, 1993.

    Article  Google Scholar 

  72. Vaidya, PM, “Geometry Helps in Matching”, SIAM J Comput, 18(6), pp. 1201–1224, 1989.

    Article  MathSciNet  MATH  Google Scholar 

  73. van Otterloo, PJ, A Contour-Oriented Approach to Shape Analysis, Hemel Hampstead, Prentice Hall, 1992.

    Google Scholar 

  74. Veitkamp, RC, “Survey of Continuities of Curves and Surfaces”, Computer Graphics Forum, 11(2), pp. 93–112, 1992.

    Article  Google Scholar 

  75. Veitkamp, RC, “Hierarchical Approximation and Localization”, Visual Computer, 14(10), pp. 471–487, 1998.

    Article  Google Scholar 

  76. Verri, A and Uras, C, “Metric-Topological Approach to Shape Recognition and Representation”, Image Vision Comput, 14, pp. 189–207, 1996.

    Article  Google Scholar 

  77. Vleugels, J and Veltkamp, RC, “Efficient Image Retrieval Through Vantage Objects”, Visual Information and Information Systems — Third International Conference VISUAL’99, Amsterdam, The Netherlands, Lecture Notes in Computer Science 1614, pp. 575-584, June 1999.

    Google Scholar 

  78. Wang, JZ, Wiederhold, G, Firschein, O, and Wei, SX, “Wavelet-Based Image Indexing Techniques With Partial Sketch Retrieval Capability”, Fourth Forum on Research and Technology Advances in Digital Libraries, IEEE, 1997.

    Google Scholar 

  79. Wolfson, HJ, “Model-Based Object Recognition by Geometric Hashing”, 1st European Conference on Computer Vision, Lecture Notes in Computer Science 427, pp. 526-536, Springer, 1990.

    Google Scholar 

  80. Wolfson, HJ and Rigoutsos, I, “Geometric Hashing: An Overview”, IEEE Comput Sci Eng, pp. 10-21, October–December, 1997.

    Google Scholar 

Download references

Authors
  1. Remco C. Veltkamp
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Michiel Hagedoorn
    View author publications

    You can also search for this author in PubMed Google Scholar

Editor information

Editors and Affiliations

  1. Leiden Institute of Advanced Computer Science, Leiden University, Niels Bohrweg 1, 2333 CA, Leiden, The Netherlands

    Michael S. Lew PhD

Rights and permissions

Reprints and permissions

Copyright information

© 2001 Springer-Verlag London

About this chapter

Cite this chapter

Veltkamp, R.C., Hagedoorn, M. (2001). State of the Art in Shape Matching. In: Lew, M.S. (eds) Principles of Visual Information Retrieval. Advances in Pattern Recognition. Springer, London. https://doi.org/10.1007/978-1-4471-3702-3_4

Download citation

  • DOI: https://doi.org/10.1007/978-1-4471-3702-3_4

  • Publisher Name: Springer, London

  • Print ISBN: 978-1-84996-868-3

  • Online ISBN: 978-1-4471-3702-3

  • eBook Packages: Springer Book Archive

Publish with us

Policies and ethics

Search

Navigation