Abstract
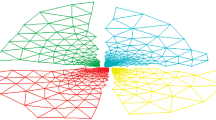
We study the effect of irregular function behavior and dynamic task partitioning on the parallel performance of the adaptive multivariate integration algorithm currently incorporated in ParInt. In view of the implicit hot spots in the computations, load balancing is essential to maintain parallel efficiency. A convergence model is given for a class of singular functions. Results are included for the computation of the cross section of a particle interaction. The adaptive meshes produced by ParInt for these problems are represented using the ParVis visualization tool.
Chapter PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
References
E. de Doncker and A. Gupta. Multivariate integration on hypercubic and mesh networks. Parallel Computing, 24:1223–1244, 1998.
Elise de Doncker, Ajay Gupta, Alan Genz, and Rodger Zanny. http://www.cs.wmich.edu/~parint, ParInt Web Site.
K. Kaugars, E. de Doncker, and R. Zanny. ParVis: Visualizing distributed dynamic partitioning algorithms. In Proceedings of the International Conference on Parallel and Distributed Processing Techniques and Applications (PDPTA’00), pages 1215–1221, 2000.
V. Kumar, A. Y. Grama, and N. R. Vempaty. Scalable load balancing techniques for parallel computers. Journal of Parallel and Distributed Computing, 22(1):60–79, 1994.
J. N. Lyness. Applications of extrapolation techniques to multidimensional quadrature of some integrand functions with a singularity. Journal of Computational Physics, 20:346–364, 1976.
K. Tobimatsu and S. Kawabata. Multi-dimensional integration routine DICE. Technical Report 85, Kogakuin University, 1998.
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2001 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
de Doncker, E., Zanny, R., Kaugars, K., Cucos, L. (2001). Performance and Irregular Behavior of Adaptive Task Partitioning. In: Alexandrov, V.N., Dongarra, J.J., Juliano, B.A., Renner, R.S., Tan, C.J.K. (eds) Computational Science - ICCS 2001. ICCS 2001. Lecture Notes in Computer Science, vol 2074. Springer, Berlin, Heidelberg. https://doi.org/10.1007/3-540-45718-6_14
Download citation
DOI: https://doi.org/10.1007/3-540-45718-6_14
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-42233-4
Online ISBN: 978-3-540-45718-3
eBook Packages: Springer Book Archive