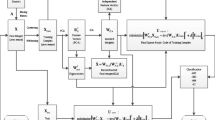
Abstract
The information-theoretic approach to face recognition is based on the compact coding where face images are decomposed into a small set of basis images. A popular method for the compact coding may be the principal component analysis (PCA) which eigenface methods are based on. PCA based methods exploit only second-order statistical structure of the data, so higher-order statistical dependencies among pixels are not considered. Factorial coding is known as one primary principle for efficient information representation and is closely related to redundancy reduction and independent component analysis (ICA). The factorial code representation exploits high-order statistical structure of the data which contains important information and is expected to give more efficient information representation, compared to eigenface methods. In this paper, we employ the factorial code representation in the reduced feature space found by the PCA and show that the factorial code representation outperforms the eigenface method in the task of face recognition. The high performance of the proposed method is confirmed by simulations.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
S. Amari. Natural gradient works efficiently in learning. Neural Computation, 10(2):251–276, Feb. 1998.
S. Amari, T. P. Chen, and A. Cichocki. Stability analysis of learning algorithms for blind source separation. Neural Networks, 10(8):1345–1351, 1997.
H. B. Barlow. Unsupervised learning. Neural Computation, 1:295–311, 1989.
M. S. Bartlett, H. M. Lades, and T. J. Sejnowski. Independent component representations for face recognition. In Proceedings of the SPIE Symposium on Electronic Imaging: Science and Technology; Conference on Human Vision and Electronic Imaging III, pages 528–539, San Jose, California, Jan. 1998.
P. N. Belhumeur, J. P. Hespanha, and D. J. Kriegman. Eigenfaces vs. Fisherfaces: Recognition using class specific linear projection. IEEE Trans. Pattern Analysis and Machine Intelligence, 19(7):711–720, Oct. 1997.
A. Bell and T. Sejnowski. An information maximisation approach to blind separation and blind deconvolution. Neural Computation, 7:1129–1159, 1995.
K. Fukunaga. An Introduction to Statistical Pattern Recognition. Academic Press, New York, NY, 1990.
A. Martinez and R. Benavente. The AR face database. Technical Report CVC #24, Computer Vision Center, Purdue University, June 1998.
E. Oja. Neural networks, principal component analysis, and subspaces. International Journal of Neural Systems, 1:61–68, 1989.
B. A. Olshausen and D. J. Field. Emergence of simple-cell receptive field properties by learning a sparse code for natural images. Nature, 381:607–609, 1996.
P. Penev and J. Atick. Local feature analysis: A general statistical theory for object representation. Network: Computation in Neural Systems, 7(3):477–500, 1996.
A. Pentland, B. Moghaddam, and T. Startner. View-based and modular eigenspaces for face recognition. In Proc. IEEE Conf. Computer Vision and Pat tern Recognition, 1994.
L. Sirovich and M. Kirby. Low-dimensional procedure for the charaterization of human faces. Journal of the Optical Society of America A, 4(3):519–524, 1987.
M. E. Tipping and C. M. Bishop. Mixtures of probabilistic principal component analyzers. Neural Computation, 11(2):443–482, 1999.
M. Turk and A. Pentland. Eigenfaces for recognition. Journal of Cognitive Neuroscience, 3(1):71–86, 1991.
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2000 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Choi, S., Lee, O. (2000). Factorial Code Representation of Faces for Recognition. In: Lee, SW., Bülthoff, H.H., Poggio, T. (eds) Biologically Motivated Computer Vision. BMCV 2000. Lecture Notes in Computer Science, vol 1811. Springer, Berlin, Heidelberg. https://doi.org/10.1007/3-540-45482-9_5
Download citation
DOI: https://doi.org/10.1007/3-540-45482-9_5
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-67560-0
Online ISBN: 978-3-540-45482-3
eBook Packages: Springer Book Archive