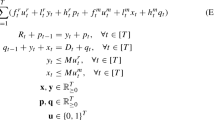Abstract
In this paper, we will consider a well-studied inventory model, called the one-warehouse multi-retailer problem (OWMR) and its special case the joint replenishment problem (JRP). As the name suggests, in this model there is one warehouse that orders a particular commodity from a supplier, in order to serve demand at N distinct retailers. We consider a discrete finite planning horizon of T periods, and are given the demand d it required for each retailer i=1,...,N in each time period t=1,...,T. There are two types of costs incurred: ordering costs (to model that there are fixed costs incurred each time the warehouse replenishes its supply on hand from the supplier, as well as the analogous cost for each retailer to be stocked from the warehouse) and holding costs (to model the fact that maintaining inventory, at both the warehouse and the retail store, incurs a cost). The aim of the model is to provide an optimization framework to balance the fact that ordering too frequently is inefficient for ordering costs, whereas ordering too rarely incurs excessive holding costs.
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Arkin, E., Joneja, D., Roundy, R.: Computational complexity of uncapacitated multi-echelon production planning problems. Operations Research Letters 8, 61–66 (1989)
Chan, A., Muriel, A., Shen, Z.-J., Simchi-Levi, D., Teo, C.-P.: Effectiveness of zero inventory ordering policies for an one-warehouse multi-retailer problem with piecewise linear cost structures. Management Science 48, 1446–1460 (2000)
Federgrun, A., Tzur, M.: Time-partitioning heuristics: Application to one warehouse, multi-item, multi-retailer lot-sizing problems. Naval Research Logistics 46, 463–486 (1999)
Levi, R., Roundy, R.O., Shmoys, D.B.: Primal-dual algorithms for deterministic inventory problems. Technical Report TR1042, ORIE Department, Cornell University (submitted, 2004)
Levi, R., Roundy, R.O., Shmoys, D.B.: Primal-dual algorithms for deterministic inventory problems. In: Proceedings of the 36th Annual ACM Symposium on Theory of Computing, pp. 353–362 (2004)
Levi, R., Shmoys, D.B., Roundy, R.O.: A constant approximation algorithm for the one-warehouse multi-retailer problem. In: Proceedings of the 15th Annual SIAM-ACM Symposium on Discrete Algorithms, pp. 365–374 (2005)
Shen, Z.J., Simchi-Levi, D., Teo, C.P.: Approximation algorithms for the single-warehouse multi-retailer problem with piecewise linear cost structures, citeseer.nj.nec.com/439759.html
Shmoys, D.B., Tardos, E., Aardal, K.I.: Approximation algorithms for facility location problems. In: Proceedings of the 29th Annual ACM Symposium on Theory of Computing, pp. 265–274 (1997)
Wagner, H.M., Whitin, T.M.: Dynamic version of the economic lot sizing model. Management Science 5, 89–96 (1958)
Zipkin, P.H.: Foundations of inventory management. The McGraw-Hill Companies, Inc., New York (2000)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2006 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Levi, R., Sviridenko, M. (2006). Improved Approximation Algorithm for the One-Warehouse Multi-Retailer Problem. In: Díaz, J., Jansen, K., Rolim, J.D.P., Zwick, U. (eds) Approximation, Randomization, and Combinatorial Optimization. Algorithms and Techniques. APPROX RANDOM 2006 2006. Lecture Notes in Computer Science, vol 4110. Springer, Berlin, Heidelberg. https://doi.org/10.1007/11830924_19
Download citation
DOI: https://doi.org/10.1007/11830924_19
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-38044-3
Online ISBN: 978-3-540-38045-0
eBook Packages: Computer ScienceComputer Science (R0)