Cerebro-cerebellar networks facilitate learning through feedback decoupling - PubMed Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2023 Jan 4;14(1):51.
doi: 10.1038/s41467-022-35658-8.

Cerebro-cerebellar networks facilitate learning through feedback decoupling

Ellen Boven #  1   2 , Joseph Pemberton #  1 , Paul Chadderton  2 , Richard Apps  2 , Rui Ponte Costa  3
Affiliations

Cerebro-cerebellar networks facilitate learning through feedback decoupling

Ellen Boven et al. Nat Commun. .

Abstract

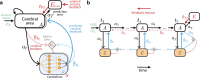
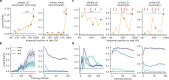
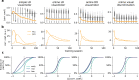
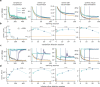
Behavioural feedback is critical for learning in the cerebral cortex. However, such feedback is often not readily available. How the cerebral cortex learns efficiently despite the sparse nature of feedback remains unclear. Inspired by recent deep learning algorithms, we introduce a systems-level computational model of cerebro-cerebellar interactions. In this model a cerebral recurrent network receives feedback predictions from a cerebellar network, thereby decoupling learning in cerebral networks from future feedback. When trained in a simple sensorimotor task the model shows faster learning and reduced dysmetria-like behaviours, in line with the widely observed functional impact of the cerebellum. Next, we demonstrate that these results generalise to more complex motor and cognitive tasks. Finally, the model makes several experimentally testable predictions regarding cerebro-cerebellar task-specific representations over learning, task-specific benefits of cerebellar predictions and the differential impact of cerebellar and inferior olive lesions. Overall, our work offers a theoretical framework of cerebro-cerebellar networks as feedback decoupling machines.

PubMed Disclaimer

Conflict of interest statement

The authors declare no competing interests.

Figures

Fig. 1
Fig. 1. Cerebro-cerebellar networks as feedback prediction machines.
a A recurrent cerebral cortical network A learns through external sensory feedback given by a task-specific prediction error module ETask computed at the end of a task fbT (top red arrow). The cerebellum aims to continuously predict the feedback expected by the cerebral network fb^t (blue) given current cerebral activity at (black). The cerebellar network (i.e. granule cells; GC and Purkinje cells; PC) learns through prediction errors (bottom red arrow) computed at the inferior olive (diamond) by comparing predicted cerebral feedback fb^t with actual cerebral feedback fbt (light blue). Shaded boxes represent multiple cerebral areas and cerebellar modules that may be interacting in parallel (see Fig. S1 for the same framework applied to decoupling across multiple brain areas). b Example of cerebro-cerebellar model unfolded in time in which the cerebral network learns to associate a cue given at t1 (x1, green) with feedback received at the end of the task, tT (cf. Fig. 2). At the end of the task the cerebral network A receives external sensory feedback fbT (red), which is transmitted to the cerebellar network as cerebral feedback fbT (light blue). Here we highlight a case of cerebral feedback horizon stopping at the end of the task T, but feedback may also be available earlier in the task (dashed red arrows). The cerebellum generates cerebral feedback predictions fb^T (blue) given cerebral activity aT (black) and learns using inferior olive (diamond) error signals (red arrow). Before tT cerebral feedback may not be readily available, thus the cerebellum learns through self-predictions. In this case the inferior olive (diamond) compares old cerebellar predictions (e.g. fb^i) with the new one (e.g. fb^T) to generate cerebellar learning signals (red arrow; see main text and “Methods” section for details).
Fig. 2
Fig. 2. Cerebro-cerebellar model improves learning in a simple line drawing sensorimotor task.
a Schematic of a macaque monkey performing a simple line drawing task (top left). A cerebro-cerebellar RNN (ccRNN) in the macaque’s brain receives cue-specific input and learns to produce the desired trajectory (top right). The temporal profile of input, output (dashed gray line represents the target trajectory) and feedback are also shown (bottom right). There are six possible target lines (coloured dashed circles; plus a 7th target for which the model must remain still) and feedback (dashed gray line) is provided at a regular interval (bottom; see the “Methods” section). In the example shown the model must draw a straight line toward the green target. b Error between model output and desired target trajectories for cerebellar RNN (gray, cRNN) and cerebro-cerebellar RNN (orange, ccRNN). Insets: Model trajectory produced for all cues after learning. c Dysmetria score for cRNN and ccRNN. The dysmetria score quantifies how smooth the movement is after learning (see the “Methods” section). d Normalized model mean squared error after learning for different cerebral feedback horizons. Feedback horizon is denoted as a percentage of the total task sequence. Arrow indicates the feedback horizon used by the cerebral network in the other panels. e Euclidean distance between the cerebral RNN dynamics corresponding to the two leading cue-specific principal components. Results are given for both the cRNN (grey) and ccRNN (orange) models. Arrows highlight training sessions of cue-specific demixed principal components (dPCs) plotted on the right for early (i), early-mid (ii), mid (iii) and late (iv) learning, for both cRNN (top) and ccRNN (bottom). Dashed lines represent the trajectory of the 2D neural dynamics throughout the task (circle represents last timestep). f Normalised cue-specific explained variance of the RNN for both cRNN (gray) and ccRNN (orange). Circular plot shows the total explained variance for cue (medium-dark colours), time (light colours) and cue-time interaction (dark colours) task variables. g Euclidean distance of the cue-specific two-dimensional neural activity for the cerebellar network (orange, ccRNN model). Arrows indicate training sessions highlighted on the right (i–iv) as in (e). In contrast to the cerebral network (g) here there is no task trajectory encoded — multiple circles represent the temporal points during the task. h Normalised explained variance for cue-specific dPCs of the cerebellar network. Circular plot colour-coding same as (f). ***p < 0.001, ****p < 0.0001 (two-sided paired t-test between cRNN and ccRNN). The animal drawing used in (a) is available at https://www.scidraw.io/drawing/445 with a Creative Commons license (https://creativecommons.org/licenses/by/4.0/). Error bars represent mean ± SEM across 10 different initial conditions. Source data are provided as a Source Data file.
Fig. 3
Fig. 3. Cerebro-cerebellar model improves learning in online complex sensorimotor and sensory discrimination tasks.
a Model behaviour across three tasks using a dataset of handwritten digits, each presented sequentially to the network (Methods and main text). Online line drawing (LD) visuomotor task: given temporally varying visual input the model is trained with sparse feedback (red dots) to draw a straight line (top left). Online digit drawing (DD) visuomotor task: given temporally varying visual input the model is trained to draw a digit following a template (top middle); target trajectories are in dotted grey and model input/output is coloured by digit. Online visual discrimination task: pattern recognition variant in which the model is trained to discriminate between 10 different digits given as sequential input. A representation of the structure of the input (green), output (green; target in grey) and feedback (red) for each task is also given (bottom of each task). b Learning curves for the three tasks for both cerebral RNN (gray, cRNN), cerebro-cerebellar RNN (orange, ccRNN). The cerebral network in all tasks uses approximately cerebral feedback horizon of 10% (cf. d). c The dysmetria score quantifies the irregularity in movement during the testing phase of the model (online LD and DD visuomotor tasks) or the uncertainty in the sensory discrimination (online visual discrimination task). d ccRNN model performance relative to cRNN across different degrees of cerebral feedback horizon (ns denotes not significant: p = 0.921 in the online LD visuomotor and p = 0.567 in the online DD visuomotor). Arrow indicates the feedback horizon used in (b, c). **p < 0.001 ***p < 0.0001, ****p < 0.0001 (two-sided paired t-test between cRNN and ccRNN). Error bars represent mean ± SEM across 10 different initial conditions. Source data are provided as a Source Data file.
Fig. 4
Fig. 4. Cerebellar-mediated facilitation of learning depends on task feedback interval.
a Dysmetria score during learning for short (light red), medium (red) and long (dark red) levels of feedback interval for the simple and online LD visuomotor tasks and both models cRNN (gray) and ccRNN (orange). Degrees of redness b Difference in dysmetria score between ccRNN and cRNN for varying degrees of task feedback intervals (ns denotes not significant: p = 0.122 (30%), p = 0.268 (40%), p = 0.142 (50%) for simple LD and p = 0.444 (36%), p = 0.209 (46%) for online LD). Degrees of red in arrows indicate the respective interval as in (a) while the white arrow indicates the feedback interval used in Figs. 2 and 3. Task feedback interval is given as a percentage of the total task time. c Difference in training error between cRNN and ccRNN for varying degrees of task feedback interval (ns for simple LD: p = 0.099). d Normalised training error integrated over learning (left) and dysmetria score at end of learning (right) of ccRNN with respect to cRNN for varying degrees of cerebral feedback horizons and task feedback intervals (left: simple LD task; right: online LD task). **p < 0.01, ***p < 0.001, ****p < 0.0001 (two-sided paired t-test between cRNN and ccRNN). Error bars represent mean ± SEM across 10 different initial conditions. Source data are provided as a Source Data file.
Fig. 5
Fig. 5. Similarity between cerebellar and cerebral feedback is task and learning-dependent.
a Cerebro-cerebellar cosine similarity throughout task sequences that do not require intermediate external feedback: a simple line drawing with feedback only at the end of the task (LD end-only) and online visual discrimination (ns denotes not significant: simple LD visuomotor p = 0.212 (0%), p = 0.520 (25%); online LD visuomotor p = 0.312 (0%), p = 0.06 (25%), p = 0.067 (50%), p = 0.386 (60%). Here and in subsequent panels, red arrows indicate points in which external feedback is available. Cosine similarity throughout the tasks is calculated across all training sessions (see the “Methods” section). b Cerebro-cerebellar cosine similarity over learning for three-time points in the task: early (turquoise), mid (blue) and late (purple) in the task (cf. a). c Cerebro-cerebellar cosine similarity throughout the sequence for tasks with intermediate external feedback: simple line drawing (LD), online LD, online digitdrawing (DD). d Cerebro-cerebellar cosine similarity over learning for three different time points in the task (early, mid and late as in b). Dashed black line represents zero similarity. **p < 0.01, ***p < 0.001, ****p < 0.0001 (two-sided paired t-test between cosine similarity and zero). Error bars represent mean ± SEM across 10 different initial conditions (20 for the simple LD visuomotor end-only task). Source data are provided as a Source Data file.
Fig. 6
Fig. 6. Cerebro-cerebellar neuronal activity coupling over learning.
a Distribution of pair-wise cerebro-cerebellar absolute correlation coefficients over learning for four tasks: simple LD, online LD, online DD and online visual discrimination. Orange line shows mean correlation coefficient. Boxplot shows median (horizontal dark orange line), interquartile range (IQR; box with centre at mean); whiskers show respective quartiles extended by 1.5 × IQR, where circles denote individual outliers beyond this range. Fully fixed ccRNN (i.e. without any form of plasticity in both networks) is given for reference (dashed line). b Change in first two principal components of cerebro-cerebellar pair-wise correlation coefficients over learning (all components available in Fig. S14). c Cumulative plot of cerebro-cerebellar pairs with positive and negative changes in absolute correlation coefficients in early (session 1), mid (session 25) and late (session 80) learning. Data grouped across 10 different initial conditions, where for each condition we sample 600 active pairs for the simple LD visuomotor task and 1000 active pairs for the online tasks (see the “Methods” section). Source data are provided as a Source Data file.
Fig. 7
Fig. 7. Inactivating cerebellar output and inferior olive have a differential impact on learning.
a Complete cerebellar lesion at different points during learning. Vertical lines represent at which point during training the cerebellum was inactivated in the ccRNN model. In gray and orange are shown the baseline performances of the cerebral RNN and ccRNN, respectively. b Normalised error after cerebellar lesion throughout learning with respect to ccRNN (ns denotes not significant: simple LD visuomotor p = 0.062 (session 150), p = 0.162 (session 475)). Gray denotes normalised error for cRNN. c Complete inferior-olive lesion at different points during learning. Vertical lines represent point of lesion of the ccRNN model. In gray and orange are shown the baseline performances of the cerebral RNN and ccRNN, respectively. d Normalised error after inferior-olive lesion throughout learning with respect to ccRNN. Gray denotes normalised error for cRNN. *p < 0.05, **p < 0.01, ***p < 0.001, ****p < 0.0001 (two-sided paired t-test between ccRNN (ablation) and ccRNN (control)). Error bars represent mean ± SEM across 10 different initial conditions. Source data are provided as a Source Data file.
Fig. 8
Fig. 8. Cerebro-cerebellar model facilitates learning in a visual-language task.
a Schematic of the model used in a visual-language task. The image is first processed by a (pretrained) convolutional neural network modelling the visual cortex. The resulting feature vector is then provided to the cerebral RNN which is trained to predict the next word given the previous words of a provided “gold standard” image caption. The cerebellum module C is only applied to the cRNN. Top left: task structure with example input image and words (green), ccRNN output words (orange) and target caption (red). b Learning curves in bits per word (BPW), lower values indicate better understanding of the language on validation set for cerebral feedback horizon of four timesteps (inset shows complete learning curve). c Two example images from the validation set with corresponding model captions and gold standard captions (black). The images shown here were generated on deepAI.org for illustration purposes only. d Normalised model performance across different degrees of feedback horizon in the cerebral network (ns denotes not significant: p = 0.891 (40%), p = 0.116 (45%)). e Normalised caption score (see the “Methods” section) as a function of caption length (ns: p = 0.075 (short), p = 0.189 (medium)). *p < 0.05, **p < 0.01, ***p < 0.001, ****p < 0.0001 (two-sided paired t-test between cRNN and ccRNN). Error bars represent mean ± SEM across 10 different initial conditions. Source data are provided as a Source Data file.
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Schultz W, Dayan P, Montague PR. A neural substrate of prediction and reward. Science. 1997;275:1593–1599. doi: 10.1126/science.275.5306.1593. - DOI - PubMed
    1. Di Bernardi Luft C. Learning from feedback: the neural mechanisms of feedback processing facilitating better performance. Behav. Brain Res. 2014;261:356–368. doi: 10.1016/j.bbr.2013.12.043. - DOI - PubMed
    1. Herzog MH, Fahle M. The role of feedback in learning a vernier discrimination task. Vision Res. 1997;37:2133–2141. doi: 10.1016/S0042-6989(97)00043-6. - DOI - PubMed
    1. Wolpert DM, Ghahramani Z. Computational principles of movement neuroscience. Nat. Neurosci. 2000;3:1212–1217. doi: 10.1038/81497. - DOI - PubMed
    1. Wolpert DM, Miall RC, Kawato M. Internal models in the cerebellum. Trends Cogn. Sci. 1998;2:338–347. doi: 10.1016/S1364-6613(98)01221-2. - DOI - PubMed

Publication types