Coordinated multiplexing of information about separate objects in visual cortex
- PMID: 36444983
- PMCID: PMC9708082
- DOI: 10.7554/eLife.76452
Coordinated multiplexing of information about separate objects in visual cortex
Abstract
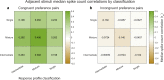
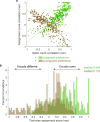
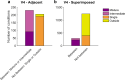
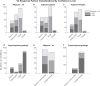
Sensory receptive fields are large enough that they can contain more than one perceptible stimulus. How, then, can the brain encode information about each of the stimuli that may be present at a given moment? We recently showed that when more than one stimulus is present, single neurons can fluctuate between coding one vs. the other(s) across some time period, suggesting a form of neural multiplexing of different stimuli (Caruso et al., 2018). Here, we investigate (a) whether such coding fluctuations occur in early visual cortical areas; (b) how coding fluctuations are coordinated across the neural population; and (c) how coordinated coding fluctuations depend on the parsing of stimuli into separate vs. fused objects. We found coding fluctuations do occur in macaque V1 but only when the two stimuli form separate objects. Such separate objects evoked a novel pattern of V1 spike count ('noise') correlations involving distinct distributions of positive and negative values. This bimodal correlation pattern was most pronounced among pairs of neurons showing the strongest evidence for coding fluctuations or multiplexing. Whether a given pair of neurons exhibited positive or negative correlations depended on whether the two neurons both responded better to the same object or had different object preferences. Distinct distributions of spike count correlations based on stimulus preferences were also seen in V4 for separate objects but not when two stimuli fused to form one object. These findings suggest multiple objects evoke different response dynamics than those evoked by single stimuli, lending support to the multiplexing hypothesis and suggesting a means by which information about multiple objects can be preserved despite the apparent coarseness of sensory coding.
Keywords: multiplexing; neuroscience; noise correlations; object vision; population coding; rhesus macaque; variability.
© 2022, Jun et al.
Conflict of interest statement
NJ, DR, LK, BB, ST, MC No competing interests declared, JG Reviewing editor, eLife
Figures


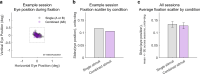
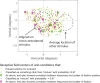

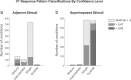

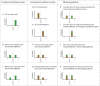


Similar articles
-
Stimulus Dependence of Correlated Variability across Cortical Areas.J Neurosci. 2016 Jul 13;36(28):7546-56. doi: 10.1523/JNEUROSCI.0504-16.2016. J Neurosci. 2016. PMID: 27413163 Free PMC article.
-
Columnar processing of border ownership in primate visual cortex.Elife. 2021 Nov 30;10:e72573. doi: 10.7554/eLife.72573. Elife. 2021. PMID: 34845986 Free PMC article.
-
Multiple objects evoke fluctuating responses in several regions of the visual pathway.bioRxiv [Preprint]. 2023 Jul 19:2023.07.19.549668. doi: 10.1101/2023.07.19.549668. bioRxiv. 2023. Update in: Elife. 2024 Mar 15;13:e91129. doi: 10.7554/eLife.91129. PMID: 37502939 Free PMC article. Updated. Preprint.
-
Neural mechanisms for stimulus selection in cortical areas of the macaque subserving object vision.Behav Brain Res. 1995 Nov;71(1-2):125-34. doi: 10.1016/0166-4328(95)00129-8. Behav Brain Res. 1995. PMID: 8747180 Review.
-
Multielectrode Recordings in the Somatosensory System.In: Nicolelis MAL, editor. Methods for Neural Ensemble Recordings. 2nd edition. Boca Raton (FL): CRC Press/Taylor & Francis; 2008. Chapter 6. In: Nicolelis MAL, editor. Methods for Neural Ensemble Recordings. 2nd edition. Boca Raton (FL): CRC Press/Taylor & Francis; 2008. Chapter 6. PMID: 21204443 Free Books & Documents. Review.
Cited by
-
Distinctive properties of biological neural networks and recent advances in bottom-up approaches toward a better biologically plausible neural network.Front Comput Neurosci. 2023 Jun 28;17:1092185. doi: 10.3389/fncom.2023.1092185. eCollection 2023. Front Comput Neurosci. 2023. PMID: 37449083 Free PMC article. Review.
-
Spike Count Analysis for MultiPlexing Inference (SCAMPI).bioRxiv [Preprint]. 2024 Sep 15:2024.09.14.613077. doi: 10.1101/2024.09.14.613077. bioRxiv. 2024. PMID: 39314268 Free PMC article. Preprint.
-
Working memory expedites the processing of visual signals within the extrastriate cortex.iScience. 2024 Jul 11;27(8):110489. doi: 10.1016/j.isci.2024.110489. eCollection 2024 Aug 16. iScience. 2024. PMID: 39100691 Free PMC article.
-
A recruitment through coherence theory of working memory.Prog Neurobiol. 2023 Sep;228:102491. doi: 10.1016/j.pneurobio.2023.102491. Epub 2023 Jun 29. Prog Neurobiol. 2023. PMID: 37393039 Free PMC article.
-
Neural basis of concurrent deliberation toward a choice and degree of confidence.bioRxiv [Preprint]. 2024 Sep 27:2024.08.06.606833. doi: 10.1101/2024.08.06.606833. bioRxiv. 2024. PMID: 39149300 Free PMC article. Preprint.
References
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources

