Developmental and evolutionary constraints on olfactory circuit selection

doi:10.1073/pnas.2100600119

. 2022 Mar 15;119(11):e2100600119.

doi: 10.1073/pnas.2100600119. Epub 2022 Mar 9.

Developmental and evolutionary constraints on olfactory circuit selection

Naoki Hiratani¹, Peter E Latham¹

Affiliations

PMID: 35263217
PMCID: PMC8931209
DOI: 10.1073/pnas.2100600119

Developmental and evolutionary constraints on olfactory circuit selection

Naoki Hiratani et al. Proc Natl Acad Sci U S A. 2022.

. 2022 Mar 15;119(11):e2100600119.

doi: 10.1073/pnas.2100600119. Epub 2022 Mar 9.

Authors

Naoki Hiratani¹, Peter E Latham¹

Affiliation

¹ Gatsby Computational Neuroscience Unit, University College London, London W1T 4JG, United Kingdom.

PMID: 35263217
PMCID: PMC8931209
DOI: 10.1073/pnas.2100600119

Abstract

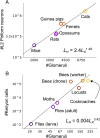
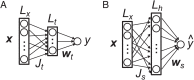
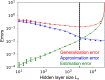
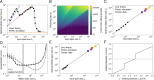
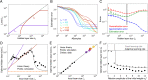
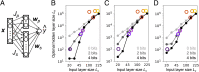
SignificanceIn this work, we explore the hypothesis that biological neural networks optimize their architecture, through evolution, for learning. We study early olfactory circuits of mammals and insects, which have relatively similar structure but a huge diversity in size. We approximate these circuits as three-layer networks and estimate, analytically, the scaling of the optimal hidden-layer size with input-layer size. We find that both longevity and information in the genome constrain the hidden-layer size, so a range of allometric scalings is possible. However, the experimentally observed allometric scalings in mammals and insects are consistent with biologically plausible values. This analysis should pave the way for a deeper understanding of both biological and artificial networks.

Keywords: model selection; neural circuit; olfaction; statistical learning theory.

PubMed Disclaimer

Conflict of interest statement

The authors declare no competing interest.

Figures

**Fig. 1.**
(A) Scaling law in mammalian olfactory circuits. Data points were taken from supplementary tables S2 and S3 of Srinivasan and Stevens (20). (B) Scaling law in invertebrate olfactory circuits. See *SI Appendix*, section 1.1 for details.

**Fig. 2.**
Network models. (A) Olfactory environment (teacher). (B) Olfactory circuit that models the environment (student).

**Fig. 3.**
Generalization error (red; Eq. 12), approximation error (blue; Eq. 9), and estimation error (green; Eq. 11) at *L_x* = 50, $N = 30, 000$ , for various hidden-layer sizes *L_h*. Lines are analytical results; points are from numerical simulations (see *SI Appendix*, section 7.4 for details). Solid and dashed vertical lines are the minima of the generalization error from theory and simulations, respectively. Here, and in all figures except Fig. 4 D and E, both *g_t* and *g_s* are rectified linear functions [ $g_{t} (u) = g_{s} (u) = \max (0, u)$ ]. In all figures except Fig. 6 we use $σ_{t}^{2} = 0.1$ for the noise in the teacher circuit, and in all figures the hidden-layer size of the teacher network is fixed at $L_{t} = 500$ . Error bars represent the SD over 10 simulations.

**Fig. 4.**
Model behavior under maximum-likelihood estimation. (A) Relationship between the input-layer size, *L_x*, and the optimal hidden-layer size, $L_{h}^{*}$ , at a fixed sample size ( $N = 30, 000$ ). Gray lines are found by optimizing Eq. 12 with respect to *L_h*; dashed lines are the asymptotic expression derived in *SI Appendix*, section 5.1. (B) Optimal hidden-layer size, $L_{h}^{*}$ , as a function of the input-layer size, *L_x*, and the sample size, N, from Eq. 12. (C) Scaling at $N = 1.65 L_{x}^{1.96}$ . Gray line is theory; black points are from simulations; colored circles are the experimental data from Fig. 1A. Simulations were done only for low *L_x*, due to the computational cost of the simulations when *L_x* is large. (D) Relationship between the hidden-layer size, *L_h*, and the generalization error, *ϵ_gen*, under the logistic activation function (black), and ReLU (gray), at *L_x* = 50 and $N = 30, 000$ . Lines are theory; bars are from simulations. Vertical lines mark the minima (solid, theory; dashed, simulations). Error bars are the SD over 10 simulations. (E) Scaling for the logistic activation function with $N = 240 L_{x}^{1.96}$ . Gray line is theory; black points are from simulations; colored circles are the experimental data from Fig. 1A. As in C, simulations were done only for low *L_x*, due to the computational cost of the simulations when *L_x* is large. (F) Analytical estimation of the $L_{h}^{*}$ - *L_x* scaling versus the *L_x*-N scaling (y axis, coefficient β in the scaling $L_{x}^{*} \propto L_{x}^{β}$ ; x axis, coefficient γ in the scaling $L_{x} \propto N^{γ}$ ; see *SI Appendix*, section 5.1 for details). The gray horizontal line is the 3/2 scaling from Fig. 1A. As in Fig. 3, the teacher network had a hidden-layer size of 500, with a ReLU nonlinearity, and the noise was set to $σ_{t}^{2} = 0.1$ .

**Fig. 5.**
Model behavior under stochastic gradient descent. (A) Hidden-layer size dependence of the decay time constant L₁ and L₂, with *L_x* = 100. (B) Dynamics of the estimation error under various hidden-layer sizes, *L_h*. Dashed lines, simulations; solid lines, theory. (C) The lifetime average generalization error, approximation error, and lifetime average estimation error under various hidden-layer sizes, *L_h*, at $N = 30, 000$ . (D) Optimal hidden-layer size, $L_{h}^{*}$ , with $N = 30, 000$ . Dashed lines are asymptotic scaling (*SI Appendix*, section 5.2). See *SI Appendix*, Fig. S2B for curves with a range of N and $σ_{t}^{2}$ . (E) Optimal hidden-layer size, $L_{h}^{*}$ , with $N = 19 L_{x}^{1.96}$ . Gray line is theory; black points are from simulations; colored circles are the experimental data from Fig. 1A. As in Fig. 4, simulations were done only for low *L_x*, due to the computational cost of the simulations when *L_x* is large. The discontinuity around $L_{x} \sim 10$ is originated from approximations that do not match perfectly around $L_{h}^{*} \sim L_{x}^{2} / 2$ (*SI Appendix*, sections 4.2 and 8). (F) Optimal hidden-layer size, $L_{h}^{*}$ , for various initial weight amplitudes, $σ_{R}^{2}$ , and $N = 30, 000$ . Gray, fixed learning rate; black, adaptive learning rate. Lines are theory and dots are simulations. The initial readout weights were sampled from $w_{s}^{(0)} \sim N (0, σ_{R}^{2} / L_{h})$ . The horizontal dashed line represents the cutoff of $L_{h}^{*}$ in the numerical simulations. When $σ_{R}^{2} < 2$ , under a fixed learning rate, $L_{h}^{*}$ is larger than 10⁵. In *A–C* and F we set the input-layer size to $L_{x} = 100$ . As in Fig. 3, the teacher network had a hidden-layer size of 500 and used a ReLU nonlinearity, and the noise was set to $σ_{t}^{2} = 0.1$ .

**Fig. 6.**
Olfactory circuit augmented with a genetically specified pathway. (A) Schematic of the two-pathway model. For the top part of the circuit, the weights $J_{p}$ and $w_{p}$ are hard wired; for the bottom part, the weights $J_{s}$ are randomly connected and $w_{s}$ are learned with adaptive SGD. (*B–D*) Optimal layer size of the projection neurons-to-Kenyon cells pathway $w_{s} \cdot g (J_{s} x)$ under different model settings. (B) Low-bit synapses were achieved by adding Gaussian noise to $J_{p}$ and $w_{p}$ . (C) Low-bit synapses were achieved by discretizing $J_{p}$ and $w_{p}$ . (D) Low-bit synapses were achieved by adding noise to $J_{p}$ and $w_{p}$ as in B, but $w_{p}$ was additionally learned from training samples using SGD (*SI Appendix*, Eq. S145). In *B–D*, the teacher network had a hidden-layer size of 500 and a ReLU nonlinearity, and we used $σ_{t}^{2} = 0.01$ and $N = 10 L_{x}^{2}$ trials. For *s_b* = 2 bits we used $G = 2, 000$ , while for *s_b* = 4 bits we used $G = 4, 000$ . For *s_b* = 0 bits, we simply removed the hard-wired pathway. The width of the hard-wired intermediate layer, *L_p*, was found from Eq. 18: $L_{p} = G / s_{b} (L_{x} + 1)$ , rounded up to an integer. See *SI Appendix*, sections 6 and 7.5 for details.

See this image and copyright information in PMC

Cited by

Input density tunes Kenyon cell sensory responses in the Drosophila mushroom body.
Ahmed M, Rajagopalan AE, Pan Y, Li Y, Williams DL, Pedersen EA, Thakral M, Previero A, Close KC, Christoforou CP, Cai D, Turner GC, Clowney EJ. Ahmed M, et al. Curr Biol. 2023 Jul 10;33(13):2742-2760.e12. doi: 10.1016/j.cub.2023.05.064. Epub 2023 Jun 21. Curr Biol. 2023. PMID: 37348501 Free PMC article.
Biologically plausible local synaptic learning rules robustly implement deep supervised learning.
Konishi M, Igarashi KM, Miura K. Konishi M, et al. Front Neurosci. 2023 Oct 11;17:1160899. doi: 10.3389/fnins.2023.1160899. eCollection 2023. Front Neurosci. 2023. PMID: 37886676 Free PMC article.
High-throughput sequencing of single neuron projections reveals spatial organization in the olfactory cortex.
Chen Y, Chen X, Baserdem B, Zhan H, Li Y, Davis MB, Kebschull JM, Zador AM, Koulakov AA, Albeanu DF. Chen Y, et al. Cell. 2022 Oct 27;185(22):4117-4134.e28. doi: 10.1016/j.cell.2022.09.038. Cell. 2022. PMID: 36306734 Free PMC article.
Hacking brain development to test models of sensory coding.
Ahmed M, Rajagopalan AE, Pan Y, Li Y, Williams DL, Pedersen EA, Thakral M, Previero A, Close KC, Christoforou CP, Cai D, Turner GC, Clowney EJ. Ahmed M, et al. bioRxiv [Preprint]. 2023 Jan 26:2023.01.25.525425. doi: 10.1101/2023.01.25.525425. bioRxiv. 2023. PMID: 36747712 Free PMC article. Preprint.
Distinctive properties of biological neural networks and recent advances in bottom-up approaches toward a better biologically plausible neural network.
Jeon I, Kim T. Jeon I, et al. Front Comput Neurosci. 2023 Jun 28;17:1092185. doi: 10.3389/fncom.2023.1092185. eCollection 2023. Front Comput Neurosci. 2023. PMID: 37449083 Free PMC article. Review.

See all "Cited by" articles

References

1. Mathis A., Herz A. V., Stemmler M., Optimal population codes for space: Grid cells outperform place cells. Neural Comput. 24, 2280–2317 (2012). - PubMed
1. Gjorgjieva J., Sompolinsky H., Meister M., Benefits of pathway splitting in sensory coding. J. Neurosci. 34, 12127–12144 (2014). - PMC - PubMed
1. Litwin-Kumar A., Harris K. D., Axel R., Sompolinsky H., Abbott L. F., Optimal degrees of synaptic connectivity. Neuron 93, 1153–1164.e7 (2017). - PMC - PubMed
1. Akaike H., A new look at the statistical model identification. IEEE Trans. Automat. Contr. 19, 716–723 (1974).
1. Baum E. B., Haussler D., “What size net gives valid generalization?” in Advances in Neural Information Processing Systems, Touretzky D., Ed. (NIPS, 1988), vol. 1, pp. 81–90.

MeSH terms

Actions
Actions
Actions
Actions
Actions
Actions
Actions
Actions
Actions
Actions
Actions
Actions
Actions

Grants and funding

WT_/Wellcome Trust/United Kingdom

LinkOut - more resources

Full Text Sources

[1] Mathis A., Herz A. V., Stemmler M., Optimal population codes for space: Grid cells outperform place cells. Neural Comput. 24, 2280–2317 (2012). - PubMed

[2] Mathis A., Herz A. V., Stemmler M., Optimal population codes for space: Grid cells outperform place cells. Neural Comput. 24, 2280–2317 (2012). - PubMed

[3] Gjorgjieva J., Sompolinsky H., Meister M., Benefits of pathway splitting in sensory coding. J. Neurosci. 34, 12127–12144 (2014). - PMC - PubMed

[4] Gjorgjieva J., Sompolinsky H., Meister M., Benefits of pathway splitting in sensory coding. J. Neurosci. 34, 12127–12144 (2014). - PMC - PubMed

[5] Litwin-Kumar A., Harris K. D., Axel R., Sompolinsky H., Abbott L. F., Optimal degrees of synaptic connectivity. Neuron 93, 1153–1164.e7 (2017). - PMC - PubMed

[6] Litwin-Kumar A., Harris K. D., Axel R., Sompolinsky H., Abbott L. F., Optimal degrees of synaptic connectivity. Neuron 93, 1153–1164.e7 (2017). - PMC - PubMed

[7] Akaike H., A new look at the statistical model identification. IEEE Trans. Automat. Contr. 19, 716–723 (1974).

[8] Akaike H., A new look at the statistical model identification. IEEE Trans. Automat. Contr. 19, 716–723 (1974).

[9] Baum E. B., Haussler D., “What size net gives valid generalization?” in Advances in Neural Information Processing Systems, Touretzky D., Ed. (NIPS, 1988), vol. 1, pp. 81–90.

[10] Baum E. B., Haussler D., “What size net gives valid generalization?” in Advances in Neural Information Processing Systems, Touretzky D., Ed. (NIPS, 1988), vol. 1, pp. 81–90.

Save citation to file

Email citation

Add to Collections

Add to My Bibliography

Your saved search

Create a file for external citation management software

Your RSS Feed

Developmental and evolutionary constraints on olfactory circuit selection

Affiliation

Developmental and evolutionary constraints on olfactory circuit selection

Authors

Affiliation

Abstract

Conflict of interest statement

Figures

Similar articles

Cited by

References

MeSH terms

Grants and funding

LinkOut - more resources

Full Text Sources