Cell-type-specific neuromodulation guides synaptic credit assignment in a spiking neural network - PubMed Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2021 Dec 21;118(51):e2111821118.
doi: 10.1073/pnas.2111821118.

Cell-type-specific neuromodulation guides synaptic credit assignment in a spiking neural network

Yuhan Helena Liu  1   2   3 , Stephen Smith  2   4 , Stefan Mihalas  5   2   3 , Eric Shea-Brown  5   2   3 , Uygar Sümbül  6
Affiliations

Cell-type-specific neuromodulation guides synaptic credit assignment in a spiking neural network

Yuhan Helena Liu et al. Proc Natl Acad Sci U S A. .

Abstract

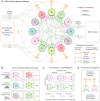
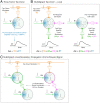
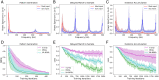
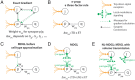
Brains learn tasks via experience-driven differential adjustment of their myriad individual synaptic connections, but the mechanisms that target appropriate adjustment to particular connections remain deeply enigmatic. While Hebbian synaptic plasticity, synaptic eligibility traces, and top-down feedback signals surely contribute to solving this synaptic credit-assignment problem, alone, they appear to be insufficient. Inspired by new genetic perspectives on neuronal signaling architectures, here, we present a normative theory for synaptic learning, where we predict that neurons communicate their contribution to the learning outcome to nearby neurons via cell-type-specific local neuromodulation. Computational tests suggest that neuron-type diversity and neuron-type-specific local neuromodulation may be critical pieces of the biological credit-assignment puzzle. They also suggest algorithms for improved artificial neural network learning efficiency.

Keywords: cell types; credit assignment; neuromodulation; neuropeptides; spiking neural network.

PubMed Disclaimer

Conflict of interest statement

The authors declare no competing interest.

Figures

Fig. 1.
Fig. 1.
MDGL network schema. (A) Six diametrically paired circles (labeled A–F) represent six types of spiking neurons, each defining a population of units on the basis of differential synaptic and modulatory connection and affinity statistics. Inhibitory and excitatory synaptic connections are cartooned here by faint curving lines, while both TD and local modulatory connections are indicated by arrow-spray glyphs representing secretion of TD and local modulatory ligands and activation of modulatory GPCRs, all differentially color coded as captioned. Learning tasks are defined by temporal patterns of the indicated spike inputs and outputs, as described in Fig. 3. (B) Six cell types based on excitatory vs. inhibitory synaptic actions, regular vs. adaptive spiking, and internal-only vs. output connectivity. Excitatory and inhibitory cells are further distinguished by which NP-like modulators they secrete, while only output cells are directly responsive to the dopamine-like TD modulator. (C) Cell-type–specific channels of local modulatory signaling established by activity-dependent secretion of two different modulatory ligands and two differentially selective receptors. (D) An error/reward-encoding TD signal impacts target neurons and synapses both 1) directly via activity-dependent secretion of TD ligand and 2) indirectly via activity-dependent secretion of local modulatory ligands.
Fig. 2.
Fig. 2.
Modulator-based neo-Hebbian local learning rules. (A) A conventional three-factor local learning rule models action of a “third,” TD GPCR-activating ligand (e.g., dopamine) that governs synapse reweighting (Δw) in proportion to temporal coincidence of the two Hebbian factors (presynaptic and postsynaptic activity). Such models generally require a lingering ET to sustain information about Hebbian coincidence until arrival of the TD signal. (B) Embracing new genetic evidence for local GPCR-based modulatory machinery, the MDGL theory introduces additional factors that allow spike-dependent secretion of NP-like local modulators (LM ​​e from excitatory neurons and LMi from inhibitory neurons) to participate in governing synapse reweighting (Δw) (35). As indicated here and in Fig. 1, the present MDGL model comprises both directly TD-recipient cells (types D–F; B, Left) and non–TD-recipient cells (types A–C; B, Right). Synapse reweighting requires combined GPCR activation with a persistent ET for all cell types, but GPCRs are activated on non–TD-recipient cells only by the local modulatory ligands. (C) Propagation of TD error/reward signal via spike-dependent secretion of local modulators from both excitatory and inhibitory cell types to cells lacking direct access to TD modulatory signal. For simplicity, this schema represents only the four subscripted synapses/weights, while the full model represents many more synaptic inputs per cell.
Fig. 3.
Fig. 3.
Cell-type–specific neuromodulation guides learning across multiple tasks. (A) Learning to produce a time-resolved target output pattern. (B) A delayed match to sample task, where two cue alternatives are represented by the presence/absence of input spikes. (C) An evidence-accumulation task (29, 36). (Lower) Addition of cell-type–specific modulatory signals improves learning outcomes across tasks. In line with these results, SI Appendix, Fig. S2 shows that gradients approximated by MDGL are more similar to the exact gradients than those approximated by e-prop. Solid lines/shaded regions: mean/SD of loss curves across runs (Methods).
Fig. 4.
Fig. 4.
Spatiotemporal characteristics of local neuromodulation. (A–C) Power spectra of modulatory (Mod.input; total cell-type–specific modulatory signal detected by each cell—Eq. 21) and synaptic inputs (Syn.input; total input received through synaptic connections by each cell—Eq. 22) are compared after learning for all tasks. Solid lines denote the average, and shaded regions show the SD of power spectrum across recurrent cells. Raw input traces are included in SI Appendix, Fig. S10. (D–F) Performance degrades when neighborhood specificity of modulatory signaling (NL-MDGL) is removed so that cell-type–specific modulatory signals diffuse to all cells in the network without attenuation. Learning with spatially nonspecific modulation still outperforms that without modulatory signaling (e-prop).
Fig. 5.
Fig. 5.
Cartoon summary of learning rules explored in this work. (A) The exact gradient: Updating weight wpq, the synaptic connection strength from presynaptic neuron q to postsynaptic neuron p, involves nonlocal information inaccessible to neural circuits, i.e., the knowledge of activity (e.g., voltage s) for all distant neurons j and l in the network. This is because wpq affects the activities of many other cells through indirect connections, which will then affect the network output at subsequent time steps (Eq. 17 in Methods). (B) E-prop, a state-of-the-art biologically plausible learning rule, restricts the weight update to depend only on presynaptic and postsynaptic activity and TD learning signal, as in a three-factor learning rule (Fig. 2A). (C) We allow the weight update to capture dependencies within one connection step, which are omitted in e-prop. The activity of neuron j could be delivered to p through local modulatory signaling. (D) For the signaling in C to be cell-type–specific, as consistent with experimental observation in ref. and biologically plausible mechanisms, we approximate the cell-specific gain with cell-type–specific gain (Eq. 23), which leads to our MDGL. Effect of this cell-type approximation is explored in SI Appendix, Fig. S9. (E) NL-MDGL, where modulatory signal diffuses to all cells in the network without attenuation (Fig. 4).
Fig. 6.
Fig. 6.
Computational graph and gradient propagation. (A) Schematic illustration of the recurrent neural network used in this study. (B) The mathematical dependencies of input x, state s, neuron spikes z, and loss function E unwrapped across time. (C) The dependencies of state s and neuron spikes z unwrapped across time and cells. (D) The computational flow of ds/dwpq is illustrated for exact gradients computed using exact calculation (Eq. 17) (i), e-prop (ii), and our truncation in Eq. 18, where dependency within one connection step has been captured (iii). Black arrows denote the computational flow of network states, output, and the loss; for instance, the forward arrows from zt and st going to st+1 are due to the neuronal dynamics equation in Eq. 2. Green arrows denote the computational flow of ds/dwpq for various learning rules.
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. LeCun Y., Bengio Y., Hinton G., Deep learning. Nature 521, 436–444 (2015). - PubMed
    1. Sejnowski T. J., The Deep Learning Revolution (MIT Press, Cambridge, MA, 2018).
    1. Williams R. J., Zipser D., “Gradient-based learning algorithms for recurrent networks and their computational complexity” in Back-Propagation: Theory, Architectures and Applications, Chauvin Y., Rumelhart D. E., Eds. (Erlbaum, Hillsdale, NJ, 1995), pp. 433–486.
    1. Marschall O., Cho K., Savin C., A unified framework of online learning algorithms for training recurrent neural networks. J. Mach. Learn. Res. 21, 1–34 (2020). - PubMed
    1. Mujika A., Meier F., Steger A., “Approximating real-time recurrent learning with random Kronecker factors” in 32nd Conference on Neural Information Processing Systems, Bengio S., Wallach H. M., Larochelle H., Grauman K., Cesa-Bianchi N., Eds. (Curran Associates Inc., Red Hook, NY, 2018), pp. 6594–6603.

Publication types

LinkOut - more resources