Neural Coding in Spiking Neural Networks: A Comparative Study for Robust Neuromorphic Systems - PubMed Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2021 Mar 4:15:638474.
doi: 10.3389/fnins.2021.638474. eCollection 2021.

Neural Coding in Spiking Neural Networks: A Comparative Study for Robust Neuromorphic Systems

Wenzhe Guo  1   2 , Mohammed E Fouda  2   3 , Ahmed M Eltawil  2   3 , Khaled Nabil Salama  1
Affiliations

Neural Coding in Spiking Neural Networks: A Comparative Study for Robust Neuromorphic Systems

Wenzhe Guo et al. Front Neurosci. .

Abstract

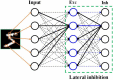
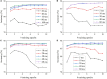
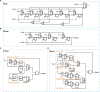
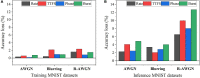
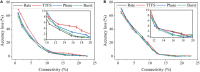
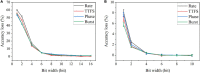
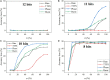
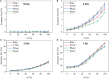
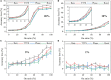
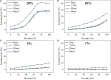
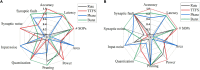
Various hypotheses of information representation in brain, referred to as neural codes, have been proposed to explain the information transmission between neurons. Neural coding plays an essential role in enabling the brain-inspired spiking neural networks (SNNs) to perform different tasks. To search for the best coding scheme, we performed an extensive comparative study on the impact and performance of four important neural coding schemes, namely, rate coding, time-to-first spike (TTFS) coding, phase coding, and burst coding. The comparative study was carried out using a biological 2-layer SNN trained with an unsupervised spike-timing-dependent plasticity (STDP) algorithm. Various aspects of network performance were considered, including classification accuracy, processing latency, synaptic operations (SOPs), hardware implementation, network compression efficacy, input and synaptic noise resilience, and synaptic fault tolerance. The classification tasks on Modified National Institute of Standards and Technology (MNIST) and Fashion-MNIST datasets were applied in our study. For hardware implementation, area and power consumption were estimated for these coding schemes, and the network compression efficacy was analyzed using pruning and quantization techniques. Different types of input noise and noise variations in the datasets were considered and applied. Furthermore, the robustness of each coding scheme to the non-ideality-induced synaptic noise and fault in analog neuromorphic systems was studied and compared. Our results show that TTFS coding is the best choice in achieving the highest computational performance with very low hardware implementation overhead. TTFS coding requires 4x/7.5x lower processing latency and 3.5x/6.5x fewer SOPs than rate coding during the training/inference process. Phase coding is the most resilient scheme to input noise. Burst coding offers the highest network compression efficacy and the best overall robustness to hardware non-idealities for both training and inference processes. The study presented in this paper reveals the design space created by the choice of each coding scheme, allowing designers to frame each scheme in terms of its strength and weakness given a designs' constraints and considerations in neuromorphic systems.

Keywords: burst coding; neural codes; neuromorphic computing; phase coding; rate coding; spiking neural networks; time to first spike coding; unsupervised learning.

PubMed Disclaimer

Conflict of interest statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Figures

FIGURE 1
FIGURE 1
SNN architecture. The input layer encodes the input pixels into spikes and is fully connected to the excitatory (Exc) neuron layer. The processing layer follows a winner-take-all principle with a special connection pattern between excitatory neurons and inhibitory (Inh) neurons, which induces lateral inhibition effect.
FIGURE 2
FIGURE 2
An illustration of neural coding schemes; (A) Rate coding, (B) Time-to-first spike coding, (C) Phase coding, and (D) Burst coding. P is the value of an input pixel. ISI is the inter-spike interval.
FIGURE 3
FIGURE 3
First row: input spike patterns of an example input digit five for different coding methods in 100 ms time window. Second row: average input spike counts over all the training input images for different coding methods in 100 ms time window.
FIGURE 4
FIGURE 4
Classification accuracy on MNIST dataset after different numbers of training epochs for different training latencies in the SNN with (A) Rate coding, (B) TTFS coding, (C) Phase coding, and (D) Burst coding.
FIGURE 5
FIGURE 5
Classification accuracy on MNIST dataset for different coding schemes at different (A) effective training latency and (B) inference latency. The effective training latency is defined as the training latency multiplied by the number of epochs required to achieve the best accuracy.
FIGURE 6
FIGURE 6
Digital implementations of different neural coding schemes; (A) Rate coding, (B) Phase coding, (C) TTFS coding, and (D) Burst coding. S and P stand for a 16-bit seed and an 8-bit input pixel. The clocks in panels (C,D) are omitted for simplicity.
FIGURE 7
FIGURE 7
Accuracy loss on MNIST dataset with different types of noise in two noisy scenarios: (A) Training with noisy datasets and inference with the no-noise dataset and (B) Training with the no-noise dataset and inference with noisy datasets.
FIGURE 8
FIGURE 8
Accuracy loss on MNIST dataset after adding the AWGN with different standard deviations, σ. (A) The noise was added to the training images, and (B) the noise was added to the inference images.
FIGURE 9
FIGURE 9
Accuracy loss on MNIST dataset changes with network connectivity resulting from weight pruning. (A) An online weight pruning method and (B) a post-training weight pruning method were considered.
FIGURE 10
FIGURE 10
Accuracy loss on MNIST dataset in the SNN with different coding schemes after weight quantization (A) during training and (B) post training.
FIGURE 11
FIGURE 11
Accuracy loss on MNIST dataset in the SNN with different coding schemes after adding programming noise to the quantized weight updates during training. The quantized bit width was changed from (A) 12 bits, (B) 11 bits, (C) 10 bits, to (D) eight bits.
FIGURE 12
FIGURE 12
Accuracy loss on MNIST dataset in the SNN with different coding schemes after adding programming noise to the quantized weights post-training for (A) eight bits, (B) four bits, (C) two bits, and (D) one bit.
FIGURE 13
FIGURE 13
Accuracy loss on MNIST dataset in the SNN with different coding schemes after considering the stuck-at-fault model during training with the fault rate of (A) 20%, (B) 10%, (C) 5%, and (D) 1%.
FIGURE 14
FIGURE 14
Accuracy loss on Fashion-MNIST dataset in the SNN with different coding schemes after considering the stuck-at-fault (SAF) model during training with the rate of (A) 20%, (B) 10%, (C) 5%, and (D) 1%.
FIGURE 15
FIGURE 15
Quantitative comparisons among different coding schemes from various aspects for (A) training and (B) inference. In each dimension, the data were normalized with the min-max normalization method. In the cases of pruning, quantization, input noise, synaptic noise, and synaptic fault, the average accuracy loss for each coding scheme was used. The greater value, the better.
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Adrian E. D., Zotterman Y. (1926). The impulses produced by sensory nerve endings: part 3. impulses set up by touch and pressure. J. Physiol. 61 465–483. 10.1113/jphysiol.1926.sp002308 - DOI - PMC - PubMed
    1. Azarfar A., Calcini N., Huang C., Zeldenrust F., Celikel T. (2018). Neural coding: a single neuron’s perspective. Neurosci. Biobehav. Rev. 94 238–247. 10.1016/j.neubiorev.2018.09.007 - DOI - PubMed
    1. Basu S., Karki M., Ganguly S., DiBiano R., Mukhopadhyay S., Gayaka S., et al. (2017). Learning sparse feature representations using probabilistic quadtrees and deep belief nets. Neural Process. Lett. 45 855–867. 10.1007/s11063-016-9556-4 - DOI
    1. Burkitt A. N. (2006). A review of the integrate-and-fire neuron model: I. homogeneous synaptic input. Biol. Cybern. 95 1–19. 10.1007/s00422-006-0068-6 - DOI - PubMed
    1. Buzsáki G. (2012). How do neurons sense a spike burst? Neuron 73 857–859. 10.1016/j.neuron.2012.02.013 - DOI - PubMed