Repeatability of Linear and Nonlinear Elastic Modulus Maps From Repeat Scans in the Breast
- PMID: 33151880
- PMCID: PMC11017922
- DOI: 10.1109/TMI.2020.3036032
Repeatability of Linear and Nonlinear Elastic Modulus Maps From Repeat Scans in the Breast
Abstract
Compression elastography allows the precise measurement of large deformations of soft tissue in vivo. From an image sequence showing tissue undergoing large deformation, an inverse problem for both the linear and nonlinear elastic moduli distributions can be solved. As part of a larger clinical study to evaluate nonlinear elastic modulus maps (NEMs) in breast cancer, we evaluate the repeatability of linear and nonlinear modulus maps from repeat measurements. Within the cohort of subjects scanned to date, 20 had repeat scans. These repeated scans were processed to evaluate NEM repeatability. In vivo data were acquired by a custom-built, digitally controlled, uniaxial compression device with force feedback from the pressure-plate. RF-data were acquired using plane-wave imaging, at a frame-rate of 200 Hz, with a ramp-and-hold compressive force of 8N, applied at 8N/sec. A 2D block-matching algorithm was used to obtain sample-level displacement fields which were then tracked at subsample resolution using 2D cross correlation. Linear and nonlinear elasticity parameters in a modified Veronda-Westmann model of tissue elasticity were estimated using an iterative optimization method. For the repeated scans, B-mode images, strain images, and linear and nonlinear elastic modulus maps are measured and compared. Results indicate that when images are acquired in the same region of tissue and sufficiently high strain is used to recover nonlinearity parameters, then the reconstructed modulus maps are consistent.
Figures
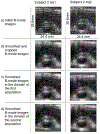
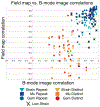
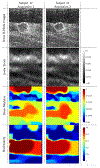
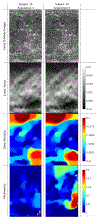
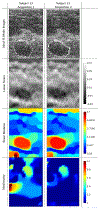
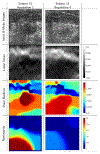
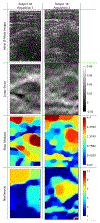
Similar articles
-
Elastic nonlinearity imaging.Annu Int Conf IEEE Eng Med Biol Soc. 2009;2009:1967-70. doi: 10.1109/IEMBS.2009.5333442. Annu Int Conf IEEE Eng Med Biol Soc. 2009. PMID: 19964024
-
Quantitative breast elastography from B-mode images.Med Phys. 2019 Jul;46(7):3001-3012. doi: 10.1002/mp.13537. Epub 2019 May 10. Med Phys. 2019. PMID: 30972759
-
An Iterative Method for Estimating Nonlinear Elastic Constants of Tumor in Soft Tissue from Approximate Displacement Measurements.J Healthc Eng. 2019 Jan 6;2019:2374645. doi: 10.1155/2019/2374645. eCollection 2019. J Healthc Eng. 2019. PMID: 30723537 Free PMC article.
-
Characterization of biomechanical properties of agar based tissue mimicking phantoms for ultrasound stiffness imaging techniques.J Mech Behav Biomed Mater. 2014 Jul;35:132-43. doi: 10.1016/j.jmbbm.2014.03.017. Epub 2014 Apr 1. J Mech Behav Biomed Mater. 2014. PMID: 24769915
-
Linear and nonlinear elastic modulus imaging: an application to breast cancer diagnosis.IEEE Trans Med Imaging. 2012 Aug;31(8):1628-37. doi: 10.1109/TMI.2012.2201497. Epub 2012 May 30. IEEE Trans Med Imaging. 2012. PMID: 22665504 Free PMC article.
Cited by
-
A Force-Matched Approach to Large-Strain Nonlinearity in Elasticity Imaging for Breast Lesion Characterization.IEEE Trans Biomed Eng. 2024 Jan;71(1):367-374. doi: 10.1109/TBME.2023.3305986. Epub 2023 Dec 22. IEEE Trans Biomed Eng. 2024. PMID: 37590110 Free PMC article.
References
-
- Moinfar F, Man YG, Arnould L, Bratthauer GL, Ratschek M, and Tavassoli FA, “Concurrent and independent genetic alterations in the stromal and epithelial cells of mammary carcinoma: implications for tumorigenesis,” Cancer Research, vol. 60, no. 9, pp. 2562–2566, 2000. - PubMed
-
- Sarvazyan AP, “Elastic properties of soft tissue,” in Handbook of elastic properties of solid, liquid and gases - Vol III: Elastic properties of solids: Biological and organical materials, earth and marine sciences, Levy Bass, and Stern, Eds. New York: Academic, 2001, ch. 5.
-
- Krouskop TA, Wheeler TM, Kallel F, Garra BS, and Hall T, “Elastic moduli of breast and prostate tissues under compression,” Ultrasonic Imaging, vol. 20, no. 4, pp. 260–274, 1998. - PubMed
-
- Berg WA et al., “Shear-wave elastography improves the specificity of breast US: the BE1 multinational study of 939 masses,” Radiology, vol. 262, no. 2, pp. 435–449, 2012. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Research Materials

