Biological batch normalisation: How intrinsic plasticity improves learning in deep neural networks - PubMed Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2020 Sep 23;15(9):e0238454.
doi: 10.1371/journal.pone.0238454. eCollection 2020.

Biological batch normalisation: How intrinsic plasticity improves learning in deep neural networks

Nolan Peter Shaw  1 , Tyler Jackson  1 , Jeff Orchard  1
Affiliations

Biological batch normalisation: How intrinsic plasticity improves learning in deep neural networks

Nolan Peter Shaw et al. PLoS One. .

Abstract

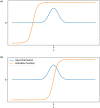
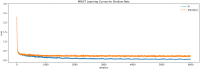
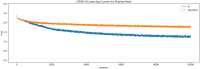
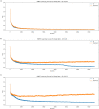
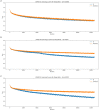
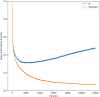
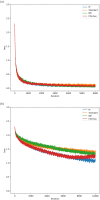
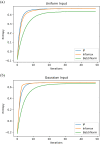
In this work, we present a local intrinsic rule that we developed, dubbed IP, inspired by the Infomax rule. Like Infomax, this rule works by controlling the gain and bias of a neuron to regulate its rate of fire. We discuss the biological plausibility of the IP rule and compare it to batch normalisation. We demonstrate that the IP rule improves learning in deep networks, and provides networks with considerable robustness to increases in synaptic learning rates. We also sample the error gradients during learning and show that the IP rule substantially increases the size of the gradients over the course of learning. This suggests that the IP rule solves the vanishing gradient problem. Supplementary analysis is provided to derive the equilibrium solutions that the neuronal gain and bias converge to using our IP rule. An analysis demonstrates that the IP rule results in neuronal information potential similar to that of Infomax, when tested on a fixed input distribution. We also show that batch normalisation also improves information potential, suggesting that this may be a cause for the efficacy of batch normalisation-an open problem at the time of this writing.

PubMed Disclaimer

Conflict of interest statement

The authors have declared that no competing interests exist.

Figures

Fig 1
Fig 1. Effect of the IP rule on the gradient of the activation function.
When the activation function is centered over its input distribution, the gradients of the activation function are much larger. Since error backpropagation uses these gradients as part of a product via the chain rule, centered activation functions propagate larger error gradients than off-center ones.
Fig 2
Fig 2. Example inputs used for experiments.
The above images are two inputs from the MNIST and CIFAR-10 datasets. (a) A hand-written five in MNIST. (b) A frog in CIFAR-10.
Fig 3
Fig 3. Learning curves for shallow networks.
The averaged learning curves for both IP and standard networks trained on MNIST across 20 epochs. Observe that the IP networks achieve higher performance (lower loss) after training than their standard counterparts.
Fig 4
Fig 4. Learning curves for shallow networks on CIFAR-10.
The averaged learning curves for both IP and standard networks trained on CIFAR-10 across 40 epochs. Again, the IP rule improves upon the performance of a standard network.
Fig 5
Fig 5. Learning curves for deep networks on MNIST.
The averaged learning curves for both IP and standard networks trained on MNIST across 20 epochs. The synaptic learning rates for each are, in order, 0.003, 0.01, 0.012.
Fig 6
Fig 6. Learning curves for deep networks on CIFAR-10.
The averaged learning curves for both IP and standard networks trained on CIFAR-10 across 40 epochs. The synaptic learning rates for each are, in order, 0.0006, 0.001, 0.0013.
Fig 7
Fig 7. Value of activation gradients.
The graph shows the average value of ∂y∂u for a particular layer during training. The fourth layer of the network (i.e. the third hidden layer), was chosen (the full network had 9 layers in total). As you can see, the gradient of y when IP is implemented is much larger than a standard network over the course of learning.
Fig 8
Fig 8. Learning curves for deep networks using Infomax, IP, and BN.
For this experiment, all three local rules had the same intrinsic learning rate of 0.0001. Again, 10 experiments were done with the results averaged. In both cases, networks that used the IP rule weremore successful than both BN and Infomax. (a) MNIST learning curves. (b) CIFAR-10 learning curves.
Fig 9
Fig 9. Neuronal information potential.
To generate these figures, the entropy of the distribution was estimated using the density histograms of the values of y as a Riemann approximation for the integral of the differential entropy. The update rules for each process were applied for multiple iterations on the same batch of 10000 samples. (a) Fixed uniforminput distribution. (b) Fixed Gaussian input distribution.
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

References

    1. Hebb DO. “The organization of behavior: A neuropsychological theory.” Psychology Press; (2005) April 11.
    1. Oja E. “Simplified neuron model as a principal component analyzer.” Journal of mathematical biology. (1982) November 1; 15(3):267–73. 10.1007/BF00275687 - DOI - PubMed
    1. Werbos PJ. “Applications of advances in nonlinear sensitivity analysis” In System modeling and optimization (1982) (pp. 762–770). Springer, Berlin, Heidelberg.
    1. Zhang W., Linden D. “The other side of the engram: experience-driven changes in neuronal intrinsic excitability.” Nature Reviews Neuroscience 4, 885–900, 2003. 10.1038/nrn1248 - DOI - PubMed
    1. Shannon CE, Weaver W. “The mathematical theory of communication.” University of Illinois press; (1998) September 1.

Grants and funding

The authors received no specific funding for this work.