Two Point Method For Robust Shear Wave Phase Velocity Dispersion Estimation of Viscoelastic Materials - PubMed Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2019 Sep;45(9):2540-2553.
doi: 10.1016/j.ultrasmedbio.2019.04.016. Epub 2019 Jun 21.

Two Point Method For Robust Shear Wave Phase Velocity Dispersion Estimation of Viscoelastic Materials

Piotr Kijanka  1 , Lukasz Ambrozinski  2 , Matthew W Urban  3
Affiliations

Two Point Method For Robust Shear Wave Phase Velocity Dispersion Estimation of Viscoelastic Materials

Piotr Kijanka et al. Ultrasound Med Biol. 2019 Sep.

Abstract

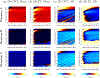
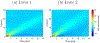
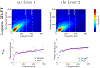
Ultrasound shear wave elastography (SWE) is an imaging modality used for noninvasive, quantitative evaluation of tissue mechanical properties. SWE uses an acoustic radiation force to produce laterally propagating shear waves that can be tracked in spatial and temporal domains in order to obtain the wave velocity. One of the ways to study the viscoelasticity is through examining the shear wave velocity dispersion curves. In this paper, we present an alternative method to two-dimensional Fourier transform (2D-FT). Our unique approach (2P-CWT) considers shear wave propagation measured in two lateral locations only and uses wavelet transformation analysis. We used the complex Morlet wavelet function as the mother wavelet to filter two shear waves at different locations. We examined how the first signal position and the distance between the two locations affect the shear wave velocity dispersion estimation in 2P-CWT. We tested this new method on a digital phantom data created using the local interaction simulation approach (LISA) in viscoelastic media with and without added white Gaussian noise to the wave motion. Moreover, we tested data acquired from custom made tissue mimicking viscoelastic phantom experiments and ex vivo porcine liver measurements. We compared results from 2P-CWT with the 2D-FT technique. 2P-CWT provided dispersion curves estimation with lower errors over a wider frequency band in comparison to 2D-FT. Tests conducted showed that the two-point technique gives results with better accuracy in simulation results and can be used to measure phase velocity of viscoelastic materials.

Keywords: Continuous wavelet transform (CWT); Shear wave elastography (SWE); Soft tissue; Ultrasound; Velocity dispersion curves; Viscoelastic; Viscosity.

PubMed Disclaimer

Figures

Figure 1:
Figure 1:
Example of reconstruction phase velocity based on the 2P-CWT approach for shear wave motion measurements. (a)temporal shear wave propagation using the particle velocity signals for selected lateral positions of 5.2 (sw1) and 8.2 (sw2) mm from the push beam location, respectively. (b) a cross-correlogram with its minimum representing the phase velocity of the shear wave. (c) extracted the phase velocity from the cross-correlogram (b) compared with the phase velocity com-puted using the 2D-FT approach.
Figure 2:
Figure 2:
Spatiotemporal shear wave propagation using the particle sig-nal velocity (a) without added noise and (b) with an SNR = 15 dB. Results were calculated for the numerical LISA viscoelastic phantoms, with assumed material properties. (top row) μ1 = 4.99 kPa and μ2 = 1 Pa·s (Phantom 1). (middle row) μ1 = 3.34 kPa and μ2 = 1.25 Pa·s (Phantom 2). (bottom row) μ1 = 1.48 kPa and μ2 = 0.75 Pa·s (Phantom 3). (bottom row) μ1 = 1.48 kPa and μ2 = 0.75 Pa s (Phantom 3).
Figure 3:
Figure 3:
Magnitude of the k-space spectra calculated using the 2D-FT method. The k-space spectra have superimposed vertical lines corresponding to 80 % (dotted line) and 90 % (dashed line) of power spectra amplitude, respectively. Results were calculated for the numerical LISA viscoelastic phantoms without added noise and with a SNR = 15 dB, with assumed material properties. (top row) μ1 = 4.99 kPa and μ2 = 1 Pa·s (Phantom 1). (middle row) μ1 = 3.34 kPa and μ2 = 1.25 Pa·s (Phantom 2). (bottom row) μ1 = 1.48 kPa and μ2 = 0.75 Pa·s (Phantom 3).
Figure 4:
Figure 4:
The RMSE calculated in a frequency range from 100 Hz to the frequency corresponding to (a), (b) 80 % and (c), (d) 90 % of the maximum power spectra amplitude presented in Fig. 3a. The RMSE was computed for (a), (c) 2P-CWT and (b), (d) 2D-FT techniques. Results were calculated for the numerical LISA viscoelastic phantoms without added noise with assumed material properties (top row) μ1 = 4.99 kPa and μ2 = 1 Pa·s (Phantom 1). (middle row) μ1 = 3.34 kPa and μ2 = 1.25 Pa·s (Phantom 2). (bottom row) μ1 = 1.48 kPa and μ2 = 0.75 Pa·s (Phantom 3).
Figure 5:
Figure 5:
The RMSE calculated in a frequency range from 100 Hz to the frequency corresponding to (a), (b) 80 % and (c), (d) 90 % of the maximum power spectra amplitude presented in Fig. 3b. The RMSE was computed for (a), (c) 2P-CWT and (b), (d) 2D-FT techniques. Results were calculated for the numerical LISA viscoelastic phantoms with a SNR = 15 dB with assumed material properties (top row) μ1 = 4.99 kPa and μ2 = 1 Pa·s (Phantom 1). (middle row) μ1 = 3.34 kPa and μ2 = 1.25 Pa·s (Phantom 2). (bottom row) μ1 = 1.48 kPa and μ2 = 0.75 Pa·s (Phantom 3).
Figure 6:
Figure 6:
Phase velocity curves computed for the 2D-FT (red stars) and 2P-CWT (blue dots) methods. Results were calculated for the numerical LISA viscoelastic phantoms without added noise and with a SNR = 15 dB, with assumed material properties. (top row) μ1 = 4.99 kPa and μ2 = 1 Pa·s (Phantom 1). (middle row) μ1 = 3.34 kPa and μ2 = 1.25 Pa·s (Phantom 2).(bottom row) μ1 = 1.48 kPa and μ2 = 0.75 P·s (Phantom 3). A comparison to the true (black, continues curves) values is made.
Figure 7:
Figure 7:
Spatiotemporal shear wave propagation using the particle ve-locity signal. Results are presented for the experimental, cus-tom made TM viscoelastic phantoms (a) Phantom A, (b) Phan-tom B and (c) Phantom C.
Figure 8:
Figure 8:
Magnitude of the k-space spectra calculated using the 2D-FT method (a) and phase velocity curves computed for the 2D-FT and 2P-CWT methods (b). Results were calculated for the experimental TM viscoelastic phantoms (top row) Phantom A, (middle row) Phantom B and (bottom row) Phantom C.
Figure 9:
Figure 9:
Mean of the phase velocity curves for the (a) 2P-CWT and (b) 2D-FT methods. Standard deviation of the phase velocity for the (c) 2P-CWT and (d) 2D-FT methods. All results were computed in a frequency range from 100 to 700 Hz. Results were calculated for the experimental TM viscoelastic phan-toms (top row) Phantom A, (middle row) Phantom B and (bottom row) Phantom C.
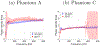
Figure 10:
Figure 10:
Mean phase velocity dispersion curves from 12 acquisitions calculated for (a) Phantom A and (b) Phantom C, respectively. Results for Phantom A were calculated for first signal position of 4 mm and distance between positions (lateral segment length) of 2 mm. Results for Phantom C were computed for first signal position of 9 mm and distance between positions (lateral segment length) of 5 mm.
Figure 11:
Figure 11:
Spatiotemporal shear wave propagation using the particle velocity signal. Results were calculated for the experimental, ex vivo liver data.
Figure 12:
Figure 12:
Top row presents magnitude of the k-space spectra calculated using the 2D-FT method. Bottom row presents phase velocity curves computed for the 2D-FT and 2P-CWT methods. Results were calculated for ex vivo liver data.
Figure 13:
Figure 13:
Mean of the phase velocity curves for the (a) 2P-CWT and (b) 2D-FT methods. Standard deviation of the phase velocity for the (c) 2P-CWT and (d) 2D-FT methods. All results were computed in a frequency range from 100 to 80% of maximum power spectra. Results were calculated for ex vivo liver data.
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Alleyne D, Cawley P. A two-dimensional fourier transform method for the measurement of propagating multimode signals. The Journal of the Acoustical Society of America, 1991;89:1159–1168.
    1. Ambrozinski L, Packo P, Pieczonka L, Stepinski T, Uhl T, Staszewski WJ. Identification of material properties e cient modelling approach based on guided wave propagation and spatial multiple signal classification. Structural Control and Health Monitoring, 2015;22:969–983.
    1. Ambrozinski L, Pelivanov I, Song S, Yoon SJ, Li D, Gao L, Shen TT, Wang RK, O’Donnell M. Air-coupled acoustic radiation force for non-contact generation of broadband mechanical waves in soft media. Applied Physics Letters, 2016a;109. - PMC - PubMed
    1. Ambrozinski L, Shaozhen Song and Yoon SJ, Pelivanov I, Li D, Gao L, Shen TT, Wang RK, O’Donnell M. Acoustic micro-tapping for non-contact 4d imaging of tissue elasticity. Scientific Reports volume, 2016b. - PMC - PubMed
    1. Bercoff J, Tanter M, Muller M, Fink M. The role of viscosity in the impulse diffraction field of elastic waves induced by the acoustic radiation force. IEEE transactions on ultrasonics, ferroelectrics, and frequency control, 2004;51:1523–1536. - PubMed

Publication types