Information-Theoretic Intrinsic Plasticity for Online Unsupervised Learning in Spiking Neural Networks - PubMed Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2019 Feb 5:13:31.
doi: 10.3389/fnins.2019.00031. eCollection 2019.

Information-Theoretic Intrinsic Plasticity for Online Unsupervised Learning in Spiking Neural Networks

Wenrui Zhang  1 , Peng Li  1
Affiliations

Information-Theoretic Intrinsic Plasticity for Online Unsupervised Learning in Spiking Neural Networks

Wenrui Zhang et al. Front Neurosci. .

Abstract

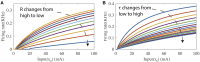
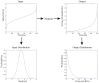
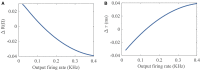
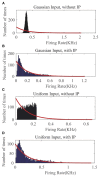
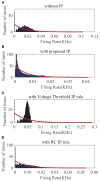
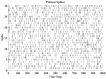
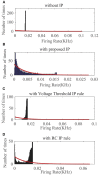
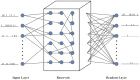
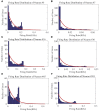
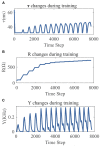
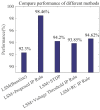
As a self-adaptive mechanism, intrinsic plasticity (IP) plays an essential role in maintaining homeostasis and shaping the dynamics of neural circuits. From a computational point of view, IP has the potential to enable promising non-Hebbian learning in artificial neural networks. While IP based learning has been attempted for spiking neuron models, the existing IP rules are ad hoc in nature, and the practical success of their application has not been demonstrated particularly toward enabling real-life learning tasks. This work aims to address the theoretical and practical limitations of the existing works by proposing a new IP rule named SpiKL-IP. SpiKL-IP is developed based on a rigorous information-theoretic approach where the target of IP tuning is to maximize the entropy of the output firing rate distribution of each spiking neuron. This goal is achieved by tuning the output firing rate distribution toward a targeted optimal exponential distribution. Operating on a proposed firing-rate transfer function, SpiKL-IP adapts the intrinsic parameters of a spiking neuron while minimizing the KL-divergence from the targeted exponential distribution to the actual output firing rate distribution. SpiKL-IP can robustly operate in an online manner under complex inputs and network settings. Simulation studies demonstrate that the application of SpiKL-IP to individual neurons in isolation or as part of a larger spiking neural network robustly produces the desired exponential distribution. The evaluation of SpiKL-IP under real-world speech and image classification tasks shows that SpiKL-IP noticeably outperforms two existing IP rules and can significantly boost recognition accuracy by up to more than 16%.

Keywords: image classification; intrinsic plasticity; liquid state machine; speech recognition; spiking neural networks; unsupervised learning.

PubMed Disclaimer

Figures

Figure 1
Figure 1
The firing-rate transfer function (FR-TF). (A) As a function of the leaky resistance R, and (B) as a function of the membrane time constant τm.
Figure 2
Figure 2
The mapping from the input current distribution to the output firing rate distributing of a neuron.
Figure 3
Figure 3
Online SpiKL-IP learning: minimization of the KL divergence at each time point during the training process.
Figure 4
Figure 4
Tuning characteristics of one-time application of SpiKL-IP at different output firing rate levels starting from a chosen combination of R and τm values R and τm. (A) Tuning of the leaky resistance R, and (B) tuning of the membrane time constant τm.
Figure 5
Figure 5
The output firing-rate distributions of a single neuron characterized using the firing-rate transfer function and driven by randomly generated current input following a Gaussian or Uniform distribution. (A) Gaussian input without IP tuning, (B) Gaussian input with the SpiKL-IP rule, (C) uniform input without IP tuning, and (D) uniform input with the SpiKL-IP rule. The red curve in each plot represents the exponential distribution that best fits the actual output firing rate data.
Figure 6
Figure 6
Output firing rate distributions of a single spiking neuron: (A) without IP tuning, (B) with proposed SpiKL-IP rule, (C) with the Voltage Threshold IP rule, and (D) with the RC IP rule. The red curve in each plot represents the exponential distribution that best fits the actual output firing rate data.
Figure 7
Figure 7
30 Poisson spike trains as input to a fully connected spiking neural network of 100 LIF neurons.
Figure 8
Figure 8
Output firing rate distributions of one spiking neuron in a fully connected network. (A) without IP tuning, (B) with proposed SpiKL-IP rule, (C) with the Voltage Threshold IP rule, and (D) with the RC IP rule. The red curve in each plot represents the exponential distribution that best fits the actual output firing rate data.
Figure 9
Figure 9
The structure of Liquid State Machine (LSM).
Figure 10
Figure 10
The output firing distributions of six reservoir neurons in an LSM after the reservoir is trained by SpiKL-IP. The red curve in each plot represents the exponential distribution the best fits the actual output firing rate data. (A) Firing rate distribution of Neuron #5, (B) Firing rate distribution of Neuron #7, (C) Firing rate distribution of Neuron #16, (D) Firing rate distribution of Neuron #36, (E) Firing rate distribution of Neuron #65, and (F) Firing rate distribution of Neuron #101.
Figure 11
Figure 11
The parameter tuning and firing rate adaption by SpiKL-IP for a reservoir neuron in an LSM during 15 iterations of training over a single speech example. (A) Tuning of the membrane time constant τm, (B) tuning of the leaky resistance R, and (C) adaptation of the Output firing rate.
Figure 12
Figure 12
Speech recognition performances of various learning rules when applied to a LSM with 135 reservoir neurons. The performance evaluation is based on the single-speaker subset of the TI46 Speech Corpus. (1) LSM (Baseline): with the settings and supervised readout learning rule in Zhang et al. (2015) and no reservoir tuning. All other compared networks add additional mechanisms to the baseline. (2) LSM+Proposed IP Rule: with additional reservoir neurons tuning using SpiKL-IP. (3) LSM+STDP: with additional reservoir neurons tuning using the STDP rule in Jin and Li (2016); (4) LSM+Voltage Threshold IP Rule: with additional reservoir neurons tuning using the IP rule in Lazar et al. (2007). (5) LSM+RC IP Rule: with additional reservoir neurons tuning using the IP rule in Li and Li (2013).
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Baddeley R., Abbott L. F., Booth M. C., Sengpiel F., Freeman T., Wakeman E. A., et al. . (1997). Responses of neurons in primary and inferior temporal visual cortices to natural scenes. Proc. R. Soc. Lond. B Biol. Sci. 264, 1775–1783. 10.1098/rspb.1997.0246 - DOI - PMC - PubMed
    1. Bell A. J., Sejnowski T. J. (1995). An information-maximization approach to blind separation and blind deconvolution. Neural Comput. 7, 1129–1159. 10.1162/neco.1995.7.6.1129 - DOI - PubMed
    1. Brunel N., Sergi S. (1998). Firing frequency of leaky intergrate-and-fire neurons with synaptic current dynamics. J. Theor. Biol. 195, 87–95. 10.1006/jtbi.1998.0782 - DOI - PubMed
    1. Cordts M., Omran M., Ramos S., Rehfeld T., Enzweiler M., Benenson R., et al. (2016). The cityscapes dataset for semantic urban scene understanding, in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 3213–3223.
    1. Dayan P., Abbott L. F. (2001). Theoretical Neuroscience, Vol. 806 Cambridge, MA: MIT Press.