In vitro neural networks minimise variational free energy - PubMed Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2018 Nov 16;8(1):16926.
doi: 10.1038/s41598-018-35221-w.

In vitro neural networks minimise variational free energy

Takuya Isomura  1 , Karl Friston  2
Affiliations

In vitro neural networks minimise variational free energy

Takuya Isomura et al. Sci Rep. .

Abstract

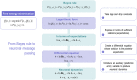
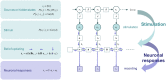
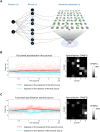
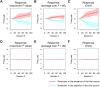
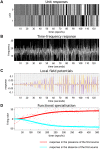
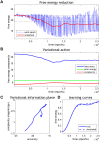
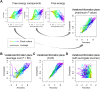
In this work, we address the neuronal encoding problem from a Bayesian perspective. Specifically, we ask whether neuronal responses in an in vitro neuronal network are consistent with ideal Bayesian observer responses under the free energy principle. In brief, we stimulated an in vitro cortical cell culture with stimulus trains that had a known statistical structure. We then asked whether recorded neuronal responses were consistent with variational message passing based upon free energy minimisation (i.e., evidence maximisation). Effectively, this required us to solve two problems: first, we had to formulate the Bayes-optimal encoding of the causes or sources of sensory stimulation, and then show that these idealised responses could account for observed electrophysiological responses. We describe a simulation of an optimal neural network (i.e., the ideal Bayesian neural code) and then consider the mapping from idealised in silico responses to recorded in vitro responses. Our objective was to find evidence for functional specialisation and segregation in the in vitro neural network that reproduced in silico learning via free energy minimisation. Finally, we combined the in vitro and in silico results to characterise learning in terms of trajectories in a variational information plane of accuracy and complexity.

PubMed Disclaimer

Conflict of interest statement

The authors declare no competing interests.

Figures

Figure 1
Figure 1
This schematic summarises the conceptual moves that provide a neuronal process theory for Bayesian belief updating with neuronal dynamics (please see Methods for a more technical and complete description). First, we start with Bayes rule, which says that the joint probability of some causes (hidden states in the world: sτ) and their consequences (observable outcomes: oτ) is the same as the probability of causes given outcomes times the probability of outcomes, which is the same as the probability of the outcomes given their causes times the probability of the causes: i.e., P(sτ,oτ)=P(sτ|oτ)P(oτ)=P(oτ|sτ)P(sτ). The second step involves taking the logarithm of these probabilistic relationships and dispensing with the probability over outcomes (because it does not change with the posterior probability of the hidden states we want to infer). Note, at this point, we have replaced the posterior probability with its approximate, free energy minimising, form: Q(sτ)≈P(sτ|oτ). The second step involves rewriting the logarithmic form in terms of the sufficient statistics or parameters of the probability distributions. For discrete state-space models, these are simply expectations (denoted by boldface). Here, we have used an empirical prior; namely, the probability of the current state given the previous state of affairs. The probability transition matrix — entailed by this empirical prior — is denoted by (B), while the likelihood matrix is denoted by (A). The fourth move is to write down a differential equation, whose solution is the posterior expectation in the middle panel (expressed as a log expectation). Effectively, this involves introducing a new variable that we will associate with voltage or depolarisation vτ, which corresponds to the log expectation of causes (sτ). Finally, we introduce an auxiliary variable called prediction error ετ that is simply the difference between the current log posterior and the prior and likelihood messages. This can be associated with presynaptic drive (from error units) that changes transmembrane potential or voltage (in principal cells); such that the posterior expectation we require is a sigmoid (i.e., activation) function of depolarisation. In other words, expectations can be treated as neuronal firing rate. In summary, starting from Bayes rule and applying a series of simple transformations, we arrive at a neuronally plausible set of differential equations that can be interpreted in terms of neuronal dynamics.
Figure 2
Figure 2
This figure illustrates the variational message passing we used to simulate idealised neuronal responses. This sort of scheme optimises sufficient statistics that encode posterior beliefs about the hidden causes of sensory data. The upper part of this figure uses a graphical model to illustrate how stimuli are generated, while the lower parts of this figure illustrates variational message passing within a neural network — using a Forney factor graph description, based upon the formulation in. In our setup, we know the hidden states generating observed stimuli — and we have empirical recordings of the sufficient statistics that encode beliefs (or expectations) about these hidden states. Please see for a detailed description of variational message passing — and accompanying learning — in this context. A more general treatment of message passing on factor graphs, as a metaphor neuronal processing, can be found in.
Figure 3
Figure 3
Estimation of blind source separation of functional specialisation from empirical responses. (A) Schematic images of hidden sources, stimuli (sensory inputs), and cultured neurons on a microelectrode array dish. Two sequences of independent binary sources generate 32 sensory stimuli through the likelihood mapping (A). The 32 stimulated sites are randomly selected in advance from an 8 × 8 grid of electrodes. Half (1, …, 16) of the electrodes are stimulated under source 1, with a probability of 3/4, or source 2, with a probability of 1/4. Whereas, the remaining (17, …, 32) electrodes are stimulated under source 1, with a probability of 1/4, or source 2, with a probability of 3/4. (B) Left: The emergence of functional specialisation at the most significant electrode, which became sensitive to the presence of the first source. The red dots correspond to epoch-specific responses when the first source is present, while the cyan dots show the response in the absence of the first source. The red and cyan lines represent the predicted responses; namely, the response associated with the explanatory variables after removal of the effects of stimulation and time. Right: The underlying functional segregation as a statistical parametric map (SPM) of the F statistic. This underscores the spatial segregation of functionally specialised responses, when testing for the emergence of selectivity (treating stimulation, non-specific fluctuations, and the other source as confounding effects). The colour scale is arbitrary. Lighter grey colour denotes a more significant effect. (C) The analysis presented in these panels is exactly the same as that shown in (A); however, in this case, the explanatory variables modelled an emerging selectivity for the second source.
Figure 4
Figure 4
Average responses over culture populations. This figure illustrates the statistical robustness of the procedures used to estimate functional specialisation. Each panel shows the mean differential responses in the presence (red line) and absence (cyan) of the first source, for each session averaged over 23 samples (i.e., cultures). The shaded area indicates the standard deviation over samples. (A) Responses obtained based on activity at an electrode with the maximum F value, corresponding to the (single culture) result in Fig. 3A. (B) Responses obtained using a within-culture average over unit activities at electrodes whose F value exceeded 80. Here, we first calculated an average response over electrodes within a culture, and then calculated an average over cultures. (C) Responses obtained using a standard canonical variate analysis (CVA) with the GLM described in the main text. This shows the emergence of functional specialisation in terms of the first canonical variate (i.e. pattern over electrodes) that becomes specialised for the first source. This canonical variate represents a linear mixture of firing rates from all electrodes, averaged over each epoch. Panels (D–F) are the same as panels (A–C), but using surrogate (randomised) source signals. The comparison of the upper and lower panels illustrates the emergence of functional specialisation when, and only when, the true sources were used.
Figure 5
Figure 5
Synthetic responses of the simulated Bayes optimal encoder. (A) Simulated firing rates for the first 128 epochs, focusing on units encoding the absence (top) and presence (bottom) of the first source. (B) The equivalent responses averaged over all neurons after band-pass filtering (white lines). These simulated local field potentials are shown on a background image of induced responses following a time frequency analysis (see for details). (C) A more detailed representation of the simulated local field potentials of the units shown in panel (A). These field potentials are the band-pass filtered firing rates of the unit encoding the posterior expectation of one source (purple line) and its absence (yellow line). (D) The resulting emergence of selective responses, plotted in the same format used in Fig. 3, where red and cyan lines express responses in the presence and absence of the first source, respectively.
Figure 6
Figure 6
Empirical free energy minimisation. (A) The resulting fluctuations in free energy. The blue line corresponds to the free energy based upon the neuronal encoding (the lines in Fig. 3) and the red line shows the average over 32 successive epochs. (B) Trajectories of free energy components after smoothing. (C) Variational information plane. (D) Trajectories of learning curves obtained from empirical (solid line) and simulated (dashed line) data.
Figure 7
Figure 7
Variational information plane analysis. (A) Trajectories of accuracy, complexity (negentropy), and free energy as a function of time or learning. These trajectories were based on the responses at the electrode with the maximum value of the F statistic. Each coloured line corresponds to a different culture. The colour indicates the time course. The black lines report the average over 23 cultures. The rightmost panel shows the corresponding trajectories in the information plane by plotting complexity against accuracy. Panels (B,C) have the same format as panel (A), but different data features were used to evaluate free energy; namely, responses obtained using a within-culture average over electrodes whose F value exceeded a threshold (B) or responses obtained using a canonical variate analysis (C). Panel (D) is the same as the information plane in panel (A), but using surrogate (i.e. randomise) sources. These null results suggest that accuracy actually fell over time to a small extent with learning.
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. von Helmholtz, H. Treatise on physiological optics (Vol. 3) (The Optical Society of America, 1925).
    1. Knill DC, Pouget A. The Bayesian brain: the role of uncertainty in neural coding and computation. Trends Neurosci. 2004;27:712–719. doi: 10.1016/j.tins.2004.10.007. - DOI - PubMed
    1. DiCarlo JJ, Zoccolan D, Rust NC. How does the brain solve visual object recognition? Neuron. 2012;73:415–434. doi: 10.1016/j.neuron.2012.01.010. - DOI - PMC - PubMed
    1. Brown GD, Yamada S, Sejnowski TJ. Independent component analysis at the neural cocktail party. Trends Neurosci. 2001;24:54–63. doi: 10.1016/S0166-2236(00)01683-0. - DOI - PubMed
    1. Mesgarani N, Chang EF. Selective cortical representation of attended speaker in multi-talker speech perception. Nature. 2012;485:233–236. doi: 10.1038/nature11020. - DOI - PMC - PubMed

Publication types