Free-energy minimization in joint agent-environment systems: A niche construction perspective - PubMed Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2018 Oct 14:455:161-178.
doi: 10.1016/j.jtbi.2018.07.002. Epub 2018 Jul 27.

Free-energy minimization in joint agent-environment systems: A niche construction perspective

Jelle Bruineberg  1 , Erik Rietveld  2 , Thomas Parr  3 , Leendert van Maanen  4 , Karl J Friston  5
Affiliations

Free-energy minimization in joint agent-environment systems: A niche construction perspective

Jelle Bruineberg et al. J Theor Biol. .

Abstract

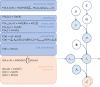
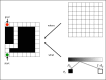
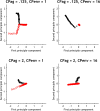
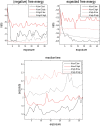
The free-energy principle is an attempt to explain the structure of the agent and its brain, starting from the fact that an agent exists (Friston and Stephan, 2007; Friston et al., 2010). More specifically, it can be regarded as a systematic attempt to understand the 'fit' between an embodied agent and its niche, where the quantity of free-energy is a measure for the 'misfit' or disattunement (Bruineberg and Rietveld, 2014) between agent and environment. This paper offers a proof-of-principle simulation of niche construction under the free-energy principle. Agent-centered treatments have so far failed to address situations where environments change alongside agents, often due to the action of agents themselves. The key point of this paper is that the minimum of free-energy is not at a point in which the agent is maximally adapted to the statistics of a static environment, but can better be conceptualized an attracting manifold within the joint agent-environment state-space as a whole, which the system tends toward through mutual interaction. We will provide a general introduction to active inference and the free-energy principle. Using Markov Decision Processes (MDPs), we then describe a canonical generative model and the ensuing update equations that minimize free-energy. We then apply these equations to simulations of foraging in an environment; in which an agent learns the most efficient path to a pre-specified location. In some of those simulations, unbeknownst to the agent, the 'desire paths' emerge as a function of the activity of the agent (i.e. niche construction occurs). We will show how, depending on the relative inertia of the environment and agent, the joint agent-environment system moves to different attracting sets of jointly minimized free-energy.

Keywords: Active inference; Adaptive environments; Agent-environment complementarity; Desire paths; Free energy principle; Markov decision processes; Niche construction.

PubMed Disclaimer

Figures

Fig 1
Fig. 1
The generative process and model and their points of contact: The generative process pertains to the causal structure of the world that generates observations for the agent, while the generative model pertains to how the agent expects the observations to be generated. A hidden state in the environment st delivers a particular observation ot to the agent. The agent then infers the most likely state of the environment (by minimizing variational free-energy) and uses its posterior expectations about hidden states to form a posterior over policies. These policies specify actions that change the state (and parameters) of the environment.
Fig 2
Fig. 2
Generative model and (approximate) posterior. Left panel: A generative model is the joint probability of outcomes o˜, hidden states s˜, policies π and parameters θ: see top equation. The model is expressed in terms of the likelihood of an observation ot given a hidden state st, and priors over hidden states: see second equation. In Markov decision processes, the likelihood is specified by an array A, parameterized by concentration parameters α. As described in Table 3, this array comprises columns of concentration parameters (of a Dirichlet distribution). These can be thought of as the number of times a particular outcome has been encountered under the hidden state associated with that column. The expected likelihood of the corresponding outcome than simply entails normalising the concentration parameters so that the sum to 1. The empirical priors over hidden states depend on the probability of hidden states at the previous time-step conditioned upon an action u (determined by policies π), these probabilistic transitions are specified by matrix B. The important aspect of this generative model is that the priors over policies P(π) are a function of expected free-energy G(π). That is to say, a priori the agent expects itself to select those policies that minimize expected free-energy G(π) (by minimizing its path integral ∑τG(π,τ)). See the main text and Table 1 for a detailed explanation of the variables. In variational Bayesian inversion, one has to specify the form of an approximate posterior distribution, which is provided in the lower panel. This particular form uses a mean field approximation, in which posterior beliefs are approximated by the product of marginal distributions Q(st|π) over unknown quantities. Here, a mean field approximation is applied to both posterior beliefs at different points in time Q(st|π), policies Q(π), parameters Q(A) and precision Q(γ). Right panel: This Bayesian graph represents the conditional dependencies that constitute the generative model. Blue circles are random variables that need to be inferred, while orange denotes observable outcomes. An arrow between circles denotes a conditional dependency, while the lack of an arrow denotes a conditional independency, which allows the factorization of the generative model, as specified on the left panel.
Fig 3
Fig. 3
The layout of the environment: The agent's environment comprises an 8 × 8 grid. At each square the agent observes its current location (‘where’ hidden state) and either an ‘open’ or ‘closed’ state (‘what’ hidden state). The mapping from hidden states to observations in the ‘where’ modality is direct (i.e., one-to-one). In the ‘what’ modality, the statistics of the environment are given by the A-matrix. An outcome is generated probabilistically based on the elements of the A-matrix at a particular location. The agent starts at the left bottom corner of the grid (green circle) and needs to go to the left top corner (red circle). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
Fig 4
Fig. 4
Exemplar trials: The left column shows the layout of the environment (A-matrix) and the right column shows the agent's expectations about the environment (A-matrix). The rows show the starting condition and the location after each trial. The green, red and blue circles designate the starting, target and final position respectively. The red-dotted line shows the agent's trajectory at other moves within a trial. In this and all subsequent examples, each trial comprised 16 moves. This figure illustrates four consecutive trials and consequent changes in the likelihood matrices that constitute the generative process (i.e. environment) and model (i.e. agent).
Fig 5
Fig. 5
Dependency on concentration parameters: The figures show the environment (in terms of the likelihood of outcomes at each location) and trajectories (top) and expectations (bottom) after the 4th trial for agents with prior concentration parameters of 1/8, 1/2, and 2 respectively. The expected likelihood (lower row) reports the agent's expectations about the environment (i.e., the expected probability of an open – white – or closed – black – outcome). We see here that with low priors the agent is more sensitive to the outcomes afforded by interaction with the environment and quickly identifies the shortest path to the target that is allowed by the environment. However, as the agent's prior precision increases, it requires more evidence to update its beliefs; giving the environment a chance to respond to the agent's beliefs and subsequent action. In this case, a ‘desire’ path (i.e. shortcut) is starting to emerge after just four trials (see upper right panel). We focus on this phenomenon in the next figure.
Fig 6
Fig. 6
Dependency on concentration parameters of the agent and environment: This figure shows the layout of the environment (A-matrix) and the agent's expectations about the environment (A-matrix) at the end of the 4th trial, as a function of the prior concentration parameters of both the agent and the environment. The left and right columns show the trajectory for high and low learning rates for the agent (with prior concentration parameters of 1/8 and 2), respectively. The top and bottom row show the trajectory for high and low learning rates of the environment (prior concentration parameters of 1 and 16), respectively. Note the unambiguous emergence of a ‘desire’ path in all scenarios apart from an environment with high concentration parameters and an agent with low concentration parameters (bottom left); i.e., an agent who is willing to learn but an environment that is not yielding. The most unambiguous desire path is clearly evident when the agent is relatively fastidious (with high prior concentration parameters) and the environment is compliant (with low concentration parameters (upper right).
Fig 7
Fig. 7
Trajectories of agent and environment in phenotypic space: the phenotypic space is defined by the first two eigenvectors of the covariances among the expectations of (both agent and environment) of an open outcome, at each location, over time. The upper and lower panels show the trajectory for low and high prior precision for the agent (with initial concentration parameters of 1/8 and 2), respectively. The left and right panels show the trajectory for low and high prior precision of the environment (with initial concentration parameters of 1 and 16), respectively. Open and closed circles designate the environment and the agent respectively, while the grey scale designates the evolution over time. In this example, the trajectories converge to the same point in phenotypic belief space because the expectations were expressed as deviations from the respective final expectations of the agent and environment.
Fig 8
Fig. 8
Temporal evolution of variational and expected free energy: these graphs report the progressive changes in (negative) variational and expected free energy (upper panels) and simulated reaction times (lower panel) averaged over 16 moves of 32 successive exposures to the environment. The results are shown for an agent with low (solid lines) and high (dotted lines) prior concentration parameters or confidence in its beliefs – in environments with low (black lines) and high (red lines) prior concentration parameters (red lines). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Allen M., Friston K.J. From cognitivism to autopoiesis: Towards a computational framework for the embodied mind. Synthese. 2016:1–24. - PMC - PubMed
    1. Ball K., Sekuler R. A specific and enduring improvement in visual motion discrimination. Science. 1982;218:697–698. - PubMed
    1. Baltieri M., Buckley C.L. Proc. Eur. Conf. on Artificial Life. 2017. An active inference implementation of phototaxis; pp. 36–43.
    1. Beal M.J. Doctoral Dissertation. University College; London: 2003. Variational algorithms for approximate Bayesian inference.
    1. Bruineberg J., Kiverstein J., Rietveld E. The anticipating brain is not a scientist: the free-energy principle from an ecological-enactive perspective. Synthese. 2016 - PMC - PubMed

Publication types

LinkOut - more resources