The Computational Anatomy of Visual Neglect - PubMed Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2018 Feb 1;28(2):777-790.
doi: 10.1093/cercor/bhx316.

The Computational Anatomy of Visual Neglect

Thomas Parr  1 , Karl J Friston  1
Affiliations

The Computational Anatomy of Visual Neglect

Thomas Parr et al. Cereb Cortex. .

Abstract

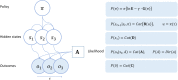
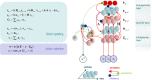
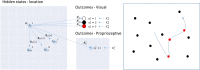
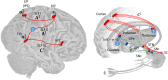
Visual neglect is a debilitating neuropsychological phenomenon that has many clinical implications and-in cognitive neuroscience-offers an important lesion deficit model. In this article, we describe a computational model of visual neglect based upon active inference. Our objective is to establish a computational and neurophysiological process theory that can be used to disambiguate among the various causes of this important syndrome; namely, a computational neuropsychology of visual neglect. We introduce a Bayes optimal model based upon Markov decision processes that reproduces the visual searches induced by the line cancellation task (used to characterize visual neglect at the bedside). We then consider 3 distinct ways in which the model could be lesioned to reproduce neuropsychological (visual search) deficits. Crucially, these 3 levels of pathology map nicely onto the neuroanatomy of saccadic eye movements and the systems implicated in visual neglect.

Keywords: Bayesian; active inference; neuropsychology; saccades; visual neglect.

PubMed Disclaimer

Figures

Figure 1.
Figure 1.
Markov decision process. The Bayesian network shown on the left describes the conditional dependencies in a Markov decision process (MDP). Each variable is shown in a circle, with shaded circles being observed variables. Arrows from one circle to another indicate that the probability of the second variable is conditioned on the first. The forms of these conditional distributions are given in the panel on the right. Cat means a categorical distribution, while Dir is a Dirichlet distribution. σ is a softmax (normalized exponential) function. Please see main text for a fuller explanation of the variables.
Figure 2.
Figure 2.
Variational update equations. The equations in the left panel can be obtained through a minimization of the variational free energy with respect to posterior expectations of each variable in the MDP model described in Figure 1. Each expectation is expressed as a vector, each component of which corresponds to the approximate (Q) distribution for a particular value of that variable. H is the entropy of the likelihood matrix. On the right, variables have been assigned to neuronal populations, and the connections between these populations determined from the update equations. The result closely resembles a cortical column with a corticosubcortical loop. The modulation of this loop by the precision (γ) unit, which is thought to correspond to dopaminergic activity (Friston et al. 2013) is suggestive of a nigrostriatal influence. The 2 opposing inputs to the policy unit could reflect the direct and indirect basal ganglia pathways. Notably, E (prior expectations about policies) does not depend on current beliefs about states, while G (expected free energy) is context dependent. Correspondingly, indirect pathway neurons in the striatum have relatively small dendritic trees with limited cortical input, while direct pathway neurons have very large dendritic trees (Gertler et al. 2008).
Figure 3.
Figure 3.
Generative model for the saccadic cancellation task. The structure of the particular generative model used for the saccadic cancellation task is shown on the left. See Fig. 1 for the definitions of the symbols used. The hidden states in this model are the locations in the visual field that are fixated. These are indicated by the 8 × 8 grid on the left of this figure. The start location, is specified by D. The agent may saccade to any location on the grid (three possible saccades are shown), and the particular saccade is defined by u, which selects the appropriate B matrix. Each component of this matrix defines the probability of a saccade to a given location (j,k, or l in the figure), given a current location (i in the figure). There are 2 A matrices which provide a probabilistic mapping from the hidden states to the visual (A1) or proprioceptive (A2) outcome modalities. Prior preferences are defined by the C matrices, which are defined for each modality. On the right is a depiction of the structure of the task resulting from the generative model. The dotted line is the saccade path, and this demonstrates the change from black to red of targets as they are canceled.
Figure 4.
Figure 4.
Computational anatomy and lesion sites. This schematic illustrates the proposed mapping from the computational entities implicated by the model (Figs 2 and 3) and their neuroanatomical substrates. On the left the dorsal and ventral attention networks are shown. The former involves the frontal eye fields (FEF) and posterior parietal areas in the region of the lateral intraparietal area (LIP) and intraparietal sulcus (IPS). The frontal areas of this network are assumed to represent the hidden states, corresponding to the current fixation location. The parietal component represents proprioceptive outcomes (eye position). The connection between these frontoparietal areas is the first branch of the superior longitudinal fasciculus (SLF I), mediating the likelihood mapping between the hidden states and proprioceptive outcomes (A2). The ventral attention network includes the ventral frontal cortex (VFC) and the temporoparietal junction (TPJ). These are connected by SLF III, which could carry prior preferences about visual outcomes (C1). Visual outcomes are assumed to be represented in the TPJ, which suggests the SLF II is the mapping from hidden states to visual outcomes (A1), and it is in these connections that the beliefs about the target locations are encoded. Prior preferences for proprioceptive outcomes are assigned to the pulvinar, a nucleus of the thalamus. On the right the connections from the pulvinar to the dorsal parietal cortex (LIP) are shown. These are portrayed as conveying expectations about (proprioceptive) outcomes in C2. In addition, the pathways through the basal ganglia are also shown. The policy evaluation processes shown in Figure 2 are depicted as stages in the direct pathway. In this scheme, the putamen evaluates the expected free energy, and baseline policy priors, E. These are modulated by dopaminergic inputs from the substantia nigra pars compacta , in proportion to their precision γ, and the output of the putamen is transformed by the substantia nigra pars reticulata into a distribution over policies. The simulated lesions we considered are numbered: 1—SLF II; 2—Putamen; 3—Pulvinar. As in the previous figure, red connections are excitatory, blue inhibitory, and green modulatory.
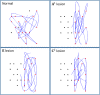
Figure 5.
Figure 5.
Simulated saccadic cancellation task. Each of the panels shows the simulated eye tracking data (blue) during 20 saccades. In all cases, the target array was the same. The upper left panel shows the performance of the model with no simulated lesions. The upper right panel shows the results when the A1 Dirichlet parameters were increased for the left hemifield, corresponding to a functional disconnection of the second branch of the right superior longitudinal fasciculus. The lower left panel shows performance when there is a biasing of policy selection, simulating a lesion of the putamen. The lower right panel represents a lesion of the prior beliefs about proprioceptive outcomes, which relates to a deficit in the inputs to the dorsal parietal cortex, likely from the pulvinar.
Figure 6.
Figure 6.
Multiscale representations of space. In the illustration on the left, 2 fixation points in a sequence of saccades are highlighted. This is to demonstrate their representation in terms of a multiscale spatial state space. In the center left, this state space is shown for each fixation point. This specifies a location in an 8 × 8 space, as before. However, the location is specified in terms of which quadrant (blue), which subquadrant (red) and which subsubquadrant (green) the location is found. These 3 specifications constitute the hidden states of the multiscale model. An advantage of this model is that it allows visual outcomes to be defined at different resolutions. This is shown in the center right. Each outcome corresponds to the density of targets in the quadrant, subquadrant, and subsubquadrant currently fixated. Darker shades indicate a greater density. Note that the finest resolution is at the level of individual locations, so density is equivalent to the presence or absence of a target. Canceled targets appear red at this level only—lower resolutions are considered to be color-blind; consistent with the properties of the magnocellular system (Hubel and Livingstone 1987). As a saccade is made from a quadrant containing 3 targets to one containing 4, the lowest resolution (blue frame) outcome becomes denser. Similarly, the subquadrant representation (red frame) becomes darker, as a subquadrant containing only one target is followed by a subquadrant containing 2. The finest resolution (green frame) represents the maximum density (one target) for both fixation locations. The illustration on the right motivates the multiscale representation in terms of the Ota task. This shows one quadrant of an array of shapes. If the blue frame was biased towards occupying the right side of the array, this would resemble an egocentric hemineglect. If the green frame were biased towards the right, this would be closer to an allocentric hemineglect.
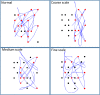
Figure 7.
Figure 7.
Lesions at different spatial scales. By changing the number of the initial Dirichlet parameters, we have simulated hemineglect at 3 resolutions. As can be seen in the above, the course scale representation biases saccades to the right side of the array, similar to the patterns seen in Figure 5. The medium scale representation biases saccades to the right side within each of the 4 quadrants of visual space. Hemineglect at the finest scale biases saccades to the right of each subquadrant (comprising 4 possible locations). For larger targets, but the same spatial scales, each of these biased sampling policies would produce results very similar to those observed in patients performing the Ota task.
Figure 8.
Figure 8.
Confusion matrices constructed from 40 saccades. The matrix on the left shows the (log) model evidence lnP(o˜|m) for each model, m (columns), given synthetic eye tracking data,o˜ generated from each model (rows). This is equivalent to the (log) likelihood or model evidence, as there were no unknown parameters. These results were generated using multiscale representations with lesions at the coarsest resolution in all cases. On the right is the matrix of posterior probabilities P(m|o˜). This is obtained from the matrix on the left, using a softmax function applied to the log evidence is in each row (i.e., for different models of each synthetic dataset).
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Adams RA, Bauer M, Pinotsis D, Friston KJ. 2016. Dynamic causal modelling of eye movements during pursuit: confirming precision-encoding in V1 using MEG. Neuroimage. 132:175–189. - PMC - PubMed
    1. Albert ML. 1973. A simple test of visual neglect. Neurology. 23:658. - PubMed
    1. Andersen RA, Essick GK, Siegel RM. 1985. Encoding of spatial location by posterior parietal neurons. Science. 230:456. - PubMed
    1. Andrade K, Samri D, Sarazin M, de Souza LC, Cohen L, Thiebaut de Schotten M, Dubois B, Bartolomeo P. 2010. Visual neglect in posterior cortical atrophy. BMC Neurol. 10:68. - PMC - PubMed
    1. Auclair L, Siéroff E, Kocer S. 2008. A case of spatial neglect dysgraphia in Wilson’s Disease. Arch Clin Neuropsychol. 23:47–62. - PubMed

Publication types