Working memory, attention, and salience in active inference - PubMed Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2017 Nov 7;7(1):14678.
doi: 10.1038/s41598-017-15249-0.

Working memory, attention, and salience in active inference

Thomas Parr  1 , Karl J Friston  2
Affiliations

Working memory, attention, and salience in active inference

Thomas Parr et al. Sci Rep. .

Abstract

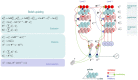
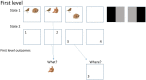
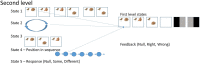
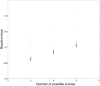
The psychological concepts of working memory and attention are widely used in the cognitive and neuroscientific literatures. Perhaps because of the interdisciplinary appeal of these concepts, the same terms are often used to mean very different things. Drawing on recent advances in theoretical neurobiology, this paper tries to highlight the correspondence between these established psychological constructs and the formal processes implicit in mathematical descriptions of brain function. Here, we consider attention and salience from the perspective offered by active inference. Using variational principles and simulations, we use active inference to demonstrate how attention and salience can be disambiguated in terms of message passing between populations of neurons in cortical and subcortical structures. In brief, we suggest that salience is something that is afforded to actions that realise epistemic affordance, while attention per se is afforded to precise sensory evidence - or beliefs about the causes of sensations.

PubMed Disclaimer

Conflict of interest statement

The authors declare that they have no competing interests.

Figures

Figure 1
Figure 1
Neuroanatomy of eye-movement control This figure illustrates the anatomy of the inputs the superior colliculus (SC) receives from the basal ganglia, noting that there is additionally a convergence of input from a diverse set of cortical regions. For clarity, other inputs to the SC have been omitted, but it should be remembered that the vestibular and cerebellar projections to the midbrain are vitally important in some aspects of saccadic control. The basal ganglia influence the SC via the substantia nigra pars reticulata (SNr), which is the point of convergence between the direct, indirect, and hyperdirect pathways. All three of these pathways are shown, with some simplifications. The direct pathway is from cortex to striatum to the SNr. The indirect is from cortex to striatum to the external segment of the globus pallidus (GPe) to the subthalamic nucleus (STN) to the SNr. The hyperdirect is from cortex to STN to SNr. The substantia nigra pars compacta (SNc) and the ventral tegmental area (VTA - not shown) of the midbrain provide a dopaminergic input to the striatum. This schematic is based on descriptions in and adapted from.
Figure 2
Figure 2
Cortical hierarchies There is a systematic, stereotyped pattern of laminar-specific connectivity in the cerebral cortex. Layer IV receives ascending (extrinsic) input, and has (intrinsic) connections to more superficial layers (II/III) in the same region. This layer provides (extrinsic) projections to layer IV in higher cortical areas and (intrinsic) connections to deep layer VI. Layer VI projects to both deep and superficial layers in lower regions, and this provides a pattern of descending (extrinsic) connections. These patterns of (extrinsic) connectivity can be used to map out hierarchies in the brain. The hierarchies in the two streams shown here ascend from the right of the image to the left. This schematic is based on the descriptions in.
Figure 3
Figure 3
Parallel cortico-subcortical loops Cortical areas target particular regions of the basal ganglia. This cortical input is the start of a loop through the basal ganglia, back to the same cortical area via the thalamus. For simplicity, only the direct pathway through the basal ganglia is shown in these figures. Connections from the dopaminergic midbrain are not shown, but these target the caudate and putamen. These schematics are based on.
Figure 4
Figure 4
–MDP generative models On the left is the basic structure of the MDP generative model, and on the right is a generalisation to a deep temporal hierarchical model. Arrows indicate conditional dependencies so that, for example, the arrow from s 3 to o 3 on the left indicates that o3 depends on s 3 (and only on s 3 directly) according to some probability P(o3∣s3). The absence of an arrow between two variables indicates conditional independence, which allows factorisation of the joint probability of the generative model. Note that the hierarchical model on the right includes multiple state transitions at a given level (where level is indicated by bracketed superscripts) for each single state transition at the level above. The hierarchical model introduces additional dependencies, which include making both policy and the first hidden state at one level dependent on the hidden state at the level above.
Figure 5
Figure 5
Neuronal message passing for a hierarchical MDP The belief updates are shown on the left The first two lines define error variables for states and outcomes. The former is equivalent to the definition of επ,t given in the text, but here is expressed in terms of the matrices and vectors of beliefs about states. The outcome error term is used to compute the expected free energy. The first two lines in the ‘inference’ box describe a gradient descent to optimise beliefs about sτ(i)∣π(i). To understand this intuitively, consider when the belief Q(sτ(i)∣π(i)) represents too high a probability for a given value of sτ(i). This results in a negative επ,t(i), meaning the corresponding component of νπ,t(i) will decrease with time. As the belief Q(sτ(i)∣π(i)) is a function of νπ,t(i), this will change the beliefs such that this value of sτ(i), conditioned on π (i), becomes less probable. This is a negative feedback system, examples of which are ubiquitous throughout biology. The evaluation of policies in the third line of the inference box is similar in form to the prior belief that policies will minimise expected free energy. The inclusion of the free energy is due to the fact that this is an attempt to approximate a posterior distribution, and once an observation has been made, the expected free energy at the previous time step becomes the sum of the free energy and the expected free energy. The fourth line is the Bayesian model average described in the main text. The action selection box provides the system with classical motor reflexes, as they ensure action fulfils expectations about outcomes. The graphic on the right provides a graphical (neural network) representation of these equations, where each unit represents one of the variables on the left. The resulting connections are strikingly consistent with a series of hierarchically arranged cortical columns, each of which participates in a cortico-subcortical loop (see Fig. 3). That the subcortical structures in this scheme have the role of evaluating policies is consistent with the known functional anatomy of the cortex and basal ganglia.
Figure 6
Figure 6
First level of the delay period task generative model: the first hidden state (State 1) is the current scene being presented, which can be any of the scenes shown in the upper row. The first three scenes are the possible scenes for both initial stimuli, and for probes at the end of the trial. The fourth is used for initial fixation and delay period, and the final two are retrocues. The first retrocue indicates that the first scene is likely to be the one they are tested on (although is uninformative about whether the probe will be in the remembered scenes set or not). The second indicates the probe is more likely to be the second scene. Unless stated otherwise, the retrocues had a validity of 90%. The second hidden state (State 2) is the current fixation location. The agent can look to any of the four quadrants in the visual scene, and controls this state via its associated B-matrix. The outcomes simply include a visual and a proprioceptive outcome. The arrows show an example of the outcomes that would be generated, according to the A-matrix: looking at the second location, when the first state is the second scene will generate the visual stimulus (outcome) of the cat. The proprioceptive outcome is simply mapped from the second state by an identity A-matrix (in the relevant dimensions). The stimulus images used here are reproduced from Mirza et al. 2016, with kind permission from the authors. https://creativecommons.org/licenses/by/4.0/. No changes have been made to the individual images.
Figure 7
Figure 7
Second level of delay period task generative model This level defines the temporal structure of the task, and selects the scenes (first level state 1 – see Fig. 6). State 1 at this level defines which two scenes will be presented at the start of the trial. State 2 indicates the order in which they will be presented. State 3 is the probe scene presented at the end. State 4 provides an index for the position in the temporal sequence of the trial – this hidden state increases deterministically with time. State 5 is the only state at this level that the agent has control over. It represents the report the agent makes, when presented with the probe. An example of a scene being generated as a lower level hidden state is indicated by the arrows. An outcome at this level provides feedback on the response. The agent expects to be right, and this is expressed in the model as a prior over the feedback outcomes. The stimulus images used here are reproduced from Mirza et al. 2016, with kind permission from the authors. https://creativecommons.org/licenses/by/4.0/. No changes have been made to the individual images.
Figure 8
Figure 8
An example trial This illustrates the course of one trial, with a response made at the end. Simulated saccades are shown in the upper panel, with fixations indicated by the red dots. Following an initial blank scene, the agent is presented with two scenes in sequence. The subsequent retrocue indicates that the second scene is more likely than the first to be the probe scene. After a delay the probe scene is presented and the agent responds correctly that it is the same as one of the initial scenes. The number of saccades within each scene presentation varies, depending on how many it takes to resolve uncertainty about the scene. Two saccades are sufficient for each scene as, once the agent knows the bird is in the top left, the top right corner should provide all of the necessary information to distinguish between the scenes. The simulated unit responses are shown in the middle panels. These represent the sufficient statistics of the approximate posterior beliefs, and are shown for the units representing states 1 and 3 at the second level, and those representing state 1 at the first level (please refer to Figs 6 and 7 for descriptions of these hidden states). Darker shades indicate a greater firing rate. The evolution of beliefs about states is much faster at the first level, and it is easy to match the responses here to the progression of the trial. At the second level, units representing beliefs about the initial scenes start with uniform activity across all three possibilities. On presentation of the first scene, the unit which does not include a representation of it reduces its activity, and the others increase. On presentation of the second scene, the combination of initial scenes is unambiguously inferred. The response of the relevant unit persists throughout the trial. It is this which should be compared to measured neuronal responses during an oculomotor delay period task, shown in the lower panel. In this experiment, the inter-trial interval (ITI) is shown, followed by fixation (F), a cue (C), a delay period (D), and a response (R). The increase in neuronal activity during the delay period matches that of the maintained representation of beliefs about the initial scenes in the simulation. Note that the upper panel is not synchronised to the unit responses, as the number of time steps the agent spends looking at each scene varies. In contrast, the unit responses are synchronised to one another, as is made clear by the vertical grey lines induced by the presentation of a new scene. The stimulus images used here are reproduced from Mirza et al. 2016, with kind permission from the authors. https://creativecommons.org/licenses/by/4.0/. No changes have been made to the individual images.
Figure 9
Figure 9
Changes in reaction time when the full set of possible scenes is 3, 4, or 5 Here, the simulation was run 150 times; 50 times for each number of possible scenes. In each case the actual sequence was identical, with a probe scene which was different to both initial scenes. However, the total number of scenes from which the scenes presented were drawn was varied. The reaction time is the computational time taken from the probe stimulus presentation to the response (i.e. the time taken by the computer to simulate this step).
Figure 10
Figure 10
Context dependent components of the ERP The effects of changes in context on the (simulated and real) ERP are shown here. Simulated ERPs are computed from the rate of change of neuronal activity (as shown in the unit response plots in Fig. 8). In other words, they are the ν˙ terms from the equations in Fig. 5, which simulate fluctuations in neuronal depolarisation. In order to test these effects in the simulation, the retrocue validity (in terms of the agent’s belief about how informative it is) was altered. A valid retrocue indicated the correct of the first two scenes with 90% validity, whereas an invalid retrocue had 50% validity. Clearly this is uninformative when indicating one of two options. A valid retrocue therefore defines a change in context, and the ERP simulated in this context dependent situation is shown on the upper plot in blue. The same plot shows a red line for context independent cueing, simulated with an invalid (uninformative) retrocue. In both cases, the ERP is generated from the higher level units representing the possible probes (the first units shown in Fig. 8). Note that there is an early context sensitive difference between conditions, which then reverses later on. While not exactly the same timing as in measured ERPs from frontal electrodes, shown in the lower plot, the overall pattern of a difference which then reverses later on is remarkably consistent. Homologous differences in ERP responses are highlighted by the shaded grey areas (these were regions of significant difference in the empirical data). Context dependent conditions are in blue, and context independent in red, as in the simulated plots.
Figure 11
Figure 11
ERP dependence on memory load The simulated ERPs shown in the upper plot are based on the same valid (blue) and invalid (red) retrocues as in Fig. 10. However, here we show the responses to the probe stimulus rather than the retrocue itself. There is an obvious difference between the two conditions which starts at around 300ms, highlighted in grey. In the experimental results in the lower plot a difference is shown in this region in different memory load conditions. The load conditions refer to how many items are remembered before the subject is tested on a probe. This load dependence has been shown to be abolished by retrocues, and the change in the simulated ERPs is consistent with this abolition, when moving from the invalid to valid condition.
Figure 12
Figure 12
Effects of dopamine modulation on salience Here each row shows the same trial, but with decreases in γ (β is the inverse of γ) relative to the row above, corresponding to a reduced dopaminergic response, and reduced precision of beliefs about policies. See the main text for a discussion of these behaviours. The plot on the right shows a simulated phasic dopamine burst in response to the probe stimulus at the end of the trial (at the second level of the model). The same response is shown for each value of β, to demonstrate the attenuation of the signal with decreasing γ. The stimulus images used here are reproduced from Mirza et al. 2016, with kind permission from the authors. https://creativecommons.org/licenses/by/4.0/. No changes have been made to the individual images.
Figure 13
Figure 13
The effects of volatility and observation noise on working memory representations Here a model is used which only has one hierarchical level. One hidden state is orientation, and another is whether the stimulus (e.g. oriented bar) is visible or not. The blue bar above each plot indicates the time for which a stimulus is present. The initial beliefs are set such that the agent believes the orientation is close to π radians. From time-step 4 to 5, a visible stimulus is presented at around π/2 radians. The A and B-matrices for each of the four trials have been modified to increase or decrease their precision (or a discrete analogy of this), seen by dispersion around the main diagonal in the graphical representations. The trials in the upper row have a precise A-matrix, which corresponds to a high sensory signal to noise, while the lower row has a less precise A-matrix. The left column trials have a precise B-matrix, meaning small fluctuations in orientation, while the right column trials show much greater volatility with a less precise B-matrix. The format of the responses is the same as in the middle panels of Fig. 8 and presents the posterior expectations of the bar’s orientation over 20 orientation bins (i.e., hidden states).
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Gregory RL. Perceptions as Hypotheses. Philosophical Transactions of the Royal Society of London. B, Biological Sciences. 1980;290:181. doi: 10.1098/rstb.1980.0090. - DOI - PubMed
    1. Friston K, Adams RA, Perrinet L, Breakspear M. Perceptions as Hypotheses: Saccades as Experiments. Frontiers in Psychology. 2012;3:151. - PMC - PubMed
    1. Corbetta M, et al. A Common Network of Functional Areas for Attention and Eye Movements. Neuron. 1998;21:761–773. doi: 10.1016/S0896-6273(00)80593-0. - DOI - PubMed
    1. Rizzolatti G, Riggio L, Dascola I, Umiltá C. Reorienting attention across the horizontal and vertical meridians: Evidence in favor of a premotor theory of attention. Neuropsychologia. 1987;25:31–40. doi: 10.1016/0028-3932(87)90041-8. - DOI - PubMed
    1. Deco G, Rolls ET. Attention and working memory: a dynamical model of neuronal activity in the prefrontal cortex. European Journal of Neuroscience. 2003;18:2374–2390. doi: 10.1046/j.1460-9568.2003.02956.x. - DOI - PubMed

Publication types

LinkOut - more resources