Sparse synaptic connectivity is required for decorrelation and pattern separation in feedforward networks - PubMed Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2017 Oct 24;8(1):1116.
doi: 10.1038/s41467-017-01109-y.

Sparse synaptic connectivity is required for decorrelation and pattern separation in feedforward networks

N Alex Cayco-Gajic  1 , Claudia Clopath  2 , R Angus Silver  3
Affiliations

Sparse synaptic connectivity is required for decorrelation and pattern separation in feedforward networks

N Alex Cayco-Gajic et al. Nat Commun. .

Abstract

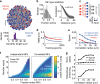
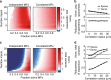
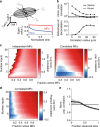
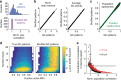
Pattern separation is a fundamental function of the brain. The divergent feedforward networks thought to underlie this computation are widespread, yet exhibit remarkably similar sparse synaptic connectivity. Marr-Albus theory postulates that such networks separate overlapping activity patterns by mapping them onto larger numbers of sparsely active neurons. But spatial correlations in synaptic input and those introduced by network connectivity are likely to compromise performance. To investigate the structural and functional determinants of pattern separation we built models of the cerebellar input layer with spatially correlated input patterns, and systematically varied their synaptic connectivity. Performance was quantified by the learning speed of a classifier trained on either the input or output patterns. Our results show that sparse synaptic connectivity is essential for separating spatially correlated input patterns over a wide range of network activity, and that expansion and correlations, rather than sparse activity, are the major determinants of pattern separation.

PubMed Disclaimer

Conflict of interest statement

The authors declare no competing financial interests.

Figures

Fig. 1
Fig. 1
A simple feedforward model of the cerebellar input layer with sparse, but not dense, synaptic connectivity speeds learning. a Top: Anatomically constrained 3D model of cerebellar input layer. Positions of Granule Cells (GCs, blue) and Mossy Fibers (MFs, red) within an 80 μm ball. Synaptic connections are shown in gray. Scale bar indicates 20 μm. Bottom: Distribution of dendritic lengths. Arrow indicates mean. b Example of MF statistics generated with a correlation radius of σ = 20 μm and average fraction of active MFs (fMF) of 0.3. Left: Histogram of the fraction of active MFs over different activity patterns. Right: Correlation between MF pairs plotted against distance between them (grey). Black indicates specified fMF (left) or specified spatial correlations (right). c Schematic of feedforward network (red, MFs; blue, GCs). The downstream perceptron-based decoder classifies either GC patterns (as shown) or else raw MF patterns without the MF-GC layer. Inset shows the rectified-linear GC transfer function. d Example of root-mean-square error as a function of the number of training epochs during learning based on MF (red) or GC (blue) activity patterns. Dashed line indicates threshold error. For this example, fMF = 0.5 and the number of inputs per GC (Nsyn) is 4. e Raw learning speed of perceptron classifier for different correlation radii, for MFs (red) or GCs with sparse (solid blue, Nsyn = 4) or dense (dashed blue, Nsyn = 16) connectivity. f Normalized learning speed (GC speed/MF speed) shown for different synaptic connectivities and fractions of active MFs. Blue lines represent double exponential fit of the boundary at which the normalized speed equals 1 (i.e., when the perceptron learning speed is the same for GC and MF activity patterns). For clarity, only the region in which the normalized speed > 1 is shown. Left: independent MF activity patterns. Right: Correlated MF inputs (σ = 20 μm). g Top: Median normalized learning speed (over different fMF) for sparse (solid line, Nsyn = 4) and dense (dashed line, Nsyn = 16) synaptic connectivities, plotted against correlation radius. Bottom: Robustness of rapid GC learning for different correlation radii
Fig. 2
Fig. 2
Cerebellar input layer sparsens and expands input activity patterns. a Normalized population sparseness (granule cell sparseness/mossy fiber sparseness) for independent mossy fiber (MF) activity patterns (left) and correlated MF inputs (right, σ = 20 μm). b Top: Median normalized population sparseness for sparse (solid line, Nsyn = 4) and dense (dashed line, Nsyn = 16) synaptic connectivities, plotted against correlation radius. Bottom: Robustness of population sparsening for different correlation radii. c, d Same as a, b plotted for normalized total variance
Fig. 3
Fig. 3
Correlations in activity increase with the extent of excitatory synaptic connectivity in feedforward networks. a Top: Illustration depicting a distribution of neural activity patterns (grey ellipsoid) in 3D activity space. Mathematically, principal lengths (black arrows) are equal to the square roots of the eigenvalues of the covariance matrix. Bottom: Example of ranked eigenvalues for mossy fiber (MF, red) and granule cell (GC, blue) activity patterns for independent MF inputs. Rank is normalized by dimensionality. Note that the MF eigenvalues are far more uniform than the GC eigenvalues, indicating that the MF patterns are less correlated. In this example, parameters are: Nsyn = 4, fMF = 0.5, σ = 0 μm. b Top: Median normalized population correlation (GC correlation/MF correlation) for sparse (solid line, Nsyn = 4) and dense (dashed line, Nsyn = 16) synaptic connectivity plotted against correlation radius. Note the logscale for the population correlation. Bottom: Robustness of GC decorrelation for different correlation radii. c Log of the normalized population correlation for independent MF activity patterns (left) and correlated MF inputs (right, σ = 20 μm). Blue region in the right panel indicates region of active decorrelation of MF patterns (defined by normalized population correlation < 1). d Log of the normalized Pearson correlation coefficient for correlated inputs (σ = 20 μm), averaged over all GC or MF pairs. e Average normalized population correlation for subpopulations of increasing size. Grey shading indicates the standard deviation across different samples and observations. For this example, Nsyn = 4 and σ = 20 μm
Fig. 4
Fig. 4
Dependence of coding space and correlation on connectivity and the role of thresholding in controlling the expansion and decorrelation. a Normalized total variance and b log normalized population correlation for networks of linear granule cells (i.e. in the absence of a threshold). Correlation radius is σ = 20 μm. c Top: robustness of expansion (green) and decorrelation (purple) for varying levels of granule cell (GC) threshold. Dotted line indicates the experimentally estimated value of threshold (3 of the 4 mossy fibers, MFs). Bottom: Robustness of learning for varying GC threshold
Fig. 5
Fig. 5
Separation of the effects of correlation on learning speed from expansion and population sparsening. a Histograms of the normalized population correlation (granule cell correlation/mossy fiber correlation) for granule cell (GC) patterns (top, blue) and shuffled GC patterns (bottom, purple). The narrow distribution around 1 indicates that the shuffled GC patterns have the same normalized population correlation as the mossy fiber (MF) patterns. b Normalized total variance (left) and average activity (right) for GC patterns (abscissa) versus shuffled GC patterns (ordinate). c Population sparseness (green) plotted for GC patterns (abscissa) and shuffled GC patterns (ordinate). Green indicates the fraction of inactive GCs for comparison as an alternate measure of population sparseness. d Raw learning speed for true GC patterns (left) and shuffled GC patterns (right). In both panels, MF inputs are correlated with a correlation radius of σ = 20 μm. e Change in learning speed due to correlations (i.e., GC speed/shuffled GC speed) plotted against the normalized population correlation. Each point represents different values of Nsyn and fMF. Correlation radii were σ = 10 μm (red) or 20 μm (black)
Fig. 6
Fig. 6
Pattern separation and learning speed depend on synaptic connectivity in biologically detailed spiking models of the cerebellar input layer. a Top: Schematic of biologically detailed spiking network model with sample spike trains. Bottom: example voltage trace from a granule cell (GC) in network. b Normalized learning speed for a spiking network with independent (left) and correlated (right, σ = 20 μm) mossy fiber (MF) activity patterns. c Normalized population sparseness (left), normalized total variance (center), and log normalized population correlation (right) for networks with different numbers of synaptic connections receiving correlated MF activity patterns (σ = 20 μm). d Median normalized learning speed plotted against correlation radius for sparse (solid, Nsyn = 4) and dense (dashed, Nsyn = 16) synaptic connectivities. e-g Same as d for normalized population sparseness e, normalized total variance f, and normalized population correlation g. h Change in learning speed due to correlations (i.e., GC speed/speed for shuffled GC spike trains) plotted against the normalized population correlation. Each point represents different values of Nsyn and fMF. Correlation radii were σ = 10 μm (red) or 20 μm (black)
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Marr D. A theory of cerebellar cortex. J. Physiol. 1969;202:437–470. doi: 10.1113/jphysiol.1969.sp008820. - DOI - PMC - PubMed
    1. Albus JS. A Theory of Cerebellar Function. Math. Biosci. 1971;10:25–61. doi: 10.1016/0025-5564(71)90051-4. - DOI
    1. Kanerva, P. Sparse Distributed Memory. (MIT Press, Cambridge, Massachusetts, 1988).
    1. Olshausen BA, Field DJ. Emergence of simple-cell receptive field properties by learning a sparse code for natural images. Nature. 1996;381:607–609. doi: 10.1038/381607a0. - DOI - PubMed
    1. Földiak, P. Sparse coding in the primate cortex. In The Handbook of Brain Theory and Neural Networks (ed. Arbib, M. A.) 1064–1068 (MIT Press, 2002).

Publication types