Deep temporal models and active inference - PubMed Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
Review
. 2017 Jun:77:388-402.
doi: 10.1016/j.neubiorev.2017.04.009. Epub 2017 Apr 14.

Deep temporal models and active inference

Karl J Friston  1 , Richard Rosch  2 , Thomas Parr  3 , Cathy Price  4 , Howard Bowman  5
Affiliations
Review

Deep temporal models and active inference

Karl J Friston et al. Neurosci Biobehav Rev. 2017 Jun.

Erratum in

  • Deep temporal models and active inference.
    Friston KJ, Rosch R, Parr T, Price C, Bowman H. Friston KJ, et al. Neurosci Biobehav Rev. 2018 Jul;90:486-501. doi: 10.1016/j.neubiorev.2018.04.004. Epub 2018 May 8. Neurosci Biobehav Rev. 2018. PMID: 29747865 Free PMC article.

Abstract

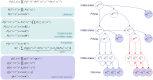
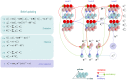
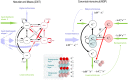
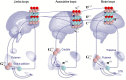
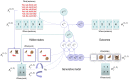
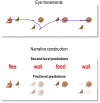
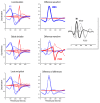
How do we navigate a deeply structured world? Why are you reading this sentence first - and did you actually look at the fifth word? This review offers some answers by appealing to active inference based on deep temporal models. It builds on previous formulations of active inference to simulate behavioural and electrophysiological responses under hierarchical generative models of state transitions. Inverting these models corresponds to sequential inference, such that the state at any hierarchical level entails a sequence of transitions in the level below. The deep temporal aspect of these models means that evidence is accumulated over nested time scales, enabling inferences about narratives (i.e., temporal scenes). We illustrate this behaviour with Bayesian belief updating - and neuronal process theories - to simulate the epistemic foraging seen in reading. These simulations reproduce perisaccadic delay period activity and local field potentials seen empirically. Finally, we exploit the deep structure of these models to simulate responses to local (e.g., font type) and global (e.g., semantic) violations; reproducing mismatch negativity and P300 responses respectively.

Keywords: Active inference; Bayesian; Free energy; Hierarchical; MMN; P300; Reading; Violation.

PubMed Disclaimer

Figures

Fig. 1
Fig. 1
Generative model and (approximate) posterior. Left panel: these equations specify the generative model. A generative model is the joint probability of outcomes or consequences and their (latent or hidden) causes, see top equation. Usually, the model is expressed in terms of a likelihood (the probability of consequences given causes) and priors over causes. When a prior depends upon a random variable it is called an empirical prior. Here, the likelihood is specified by an array A whose elements are the probability of an outcome under every combination of hidden states. The empirical priors pertain to probabilistic transitions (in the B arrays) among hidden states that can depend upon action, which is determined probabilistically by policies (sequences of actions encoded by π). The key aspect of this generative model is that policies are more probable a priori if they minimise the (path integral of) expected free energy G, which depends upon our prior preferences about outcomes encoded by the array C. Finally, the D arrays specified the initial state, given the state of the level above. This completes the specification of the model in terms of parameter arrays that constitute A, B, C and D. Bayesian model inversion refers to the inverse mapping from consequences to causes; i.e., estimating the hidden states and other variables that cause outcomes. In variational Bayesian inversion, one has to specify the form of an approximate posterior distribution, which is provided in the lower panel. This particular form uses a mean field approximation, in which posterior beliefs are approximated by the product of marginal distributions over hierarchical levels and points in time. Subscripts index time (or policy), while (bracketed) superscripts index hierarchical level. See the main text and Table 2 for a detailed explanation of the variables (italic variables represent hidden states, while bold variables indicate expectations about those states). Right panel: this Bayesian graph represents the conditional dependencies among hidden states and how they cause outcomes. Open circles are random variables (hidden states and policies) while filled circles denote observable outcomes. The key aspect of this model is its hierarchical structure that represents sequences of hidden states over time or epochs. In this model, hidden states at higher levels generate the initial states for lower levels – that then unfold to generate a sequence of outcomes: c.f., associative chaining (Page and Norris, 1998). Crucially, lower levels cycle over a sequence for each transition of the level above. This is indicated by the variables outlined in red, which are ‘reused’ as higher levels unfold. It is this scheduling that endows the model with deep temporal structure. Note that hidden states at any level can generate outcomes and hidden states at the lower level. Furthermore, the policies at each level depend upon the hidden states of the level above – and are in play for the sequence of state transitions at the level below. This means that hidden states can influence subordinate states in two ways: by specifying the initial states – or via policy-dependent state transitions. Please see main text and Table 2 for a definition of the variables. For clarity, time subscripts have been omitted from hidden states at level i + 1. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
Fig. 2
Fig. 2
Schematic overview of belief propagation: left panel: these equalities are the belief updates mediating inference (i.e. state estimation) and action selection. These expressions follow in a fairly straightforward way from a gradient descent on variational free energy. The equations have been expressed in terms of prediction errors that come in two flavours. The first, state prediction error scores the difference between the (log) expected states under any policy and time (at each hierarchical level) and the corresponding predictions based upon outcomes and the (preceding and subsequent) hidden states (1.a). These represent likelihood and empirical prior terms respectively. The prediction error drives log-expectations (2.a), where the expectation per se is obtained via a softmax operator (2.b). The second, outcome prediction error reports the difference between the (log) expected outcome and that predicted under prior preferences set by the level above (plus an ambiguity term – see appendix) (1.b). This prediction error is weighted by the expected outcomes to evaluate the expected free energy (1.d). Similarly, the free energy per se is the expected state prediction error, under current beliefs about hidden states (1.c). These policy-specific free energies are combined to give the policy expectations via a softmax function (2.c). Finally, expectations about hidden states are a Bayesian model average over expected policies (2.d) and expectations about policies specify the action that is most likely to realise the expected outcome (3). The (Iverson) brackets in Eq. (3) return one if the condition in square brackets is satisfied and zero otherwise. Right panel: this schematic represents the message passing implicit in the equations on the left. The expectations have been associated with neuronal populations (coloured balls) that are arranged to highlight the correspondence with known intrinsic (within cortical area) and extrinsic (between cortical areas) connections. Red connections are excitatory, blue connections are inhibitory and green connections are modulatory (i.e., involve a multiplication or weighting). This schematic illustrates three hierarchical levels (which are arranged horizontally in this figure, as opposed to vertically in Fig. 1), where each level provides top-down empirical priors for the initial state of the level below, while the lower level supplies evidence for the current state at the level above. The intrinsic connections mediate the empirical priors and Bayesian model averaging. Cyan units correspond to expectations about hidden states and (future) outcomes under each policy, while red states indicate their Bayesian model averages. Pink units correspond to (state and outcome) prediction errors that are averaged to evaluate (variational and expected) free energy and subsequent policy expectations (in the lower part of the network). This (neuronal) network interpretation of belief updating means that connection strengths correspond to the parameters of the generative model in Fig. 1. Please see Table 2 for a definition of the variables. The variational free energy has been omitted from this figure because the policies in this paper differ only in the next action. This means the evidence (i.e. variational free energy) from past outcomes is the same for all policies. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
Fig. 3
Fig. 3
Belief propagation and intrinsic connectivity. This schematic features the correspondence between known canonical microcircuitry and the belief updates in Fig. 2. Left Panel: a canonical microcircuit based on (Haeusler and Maass, 2007), where inhibitory cells have been omitted from the deep layers – because they have little interlaminar connectivity. The numbers denote connection strengths (mean amplitude of PSPs measured at soma in mV) and connection probabilities (in parentheses) according to (Thomson and Bannister, 2003). Right panel: the equivalent microcircuitry based upon the message passing scheme of the previous figure. Here, we have placed the outcome prediction errors in superficial layers to accommodate the strong descending (inhibitory) connections from superficial to deep layers. This presupposes that descending (interlaminar) projections disinhibit Layer 5 pyramidal cells that project to the medium spiny cells of the striatum (Arikuni and Kubota, 1986). The computational assignments in this figure should be compared with the equivalent scheme for predictive coding in (Bastos et al., 2012). The key difference is that superficial excitatory (e.g., pyramidal) cells encode expectations of hidden states, as opposed to state prediction errors. This is because the prediction error is encoded by their postsynaptic currents, as opposed to their depolarisation or firing rates (see main text). The white circles correspond to the Bayesian model average of state expectations, which are the red balls in the previous figures (and the inset). Black arrows denote excitatory intrinsic connections, while red arrows are inhibitory. Blue arrows denote bottom-up of ascending extrinsic connections, while green arrows are top-down or descending. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
Fig. 4
Fig. 4
Belief propagation and extrinsic connectivity. This schematic illustrates a putative mapping between expectations that are updated during belief updating and recurrent interactions within the cortico-basal ganglia-thalamic loops. This figure is based upon the functional neuroanatomy described in (Jahanshahi et al., 2015), which assigns motor updates to motor and premotor cortex projecting to the putamen; associative loops to prefrontal cortical projections to the caudate and limbic loops to projections to the ventral striatum. The correspondence between the message passing implicit in belief propagation and the organisation of these loops is remarkable; even down to the level of the sign (excitatory or inhibitory) of the neuronal connections. The striatum (caudate and putamen) and the subthalamic nucleus (STN) receive inputs from many cortical and subcortical areas. The internal segment of the globus pallidus (GPi) constitutes the main output nucleus from the basal ganglia. The basal ganglia are not only connected to motor areas (motor cortex, supplementary motor cortex, premotor cortex, cingulate motor area and frontal eye fields) but also have connections with associative cortical areas. The basal ganglia nuclei have topologically organized motor, associative and limbic territories; the posterior putamen is engaged in sensorimotor function, while the anterior putamen (or caudate) and the ventral striatum are involved in associative (cognitive) and limbic (motivation and emotion) functions (Jahanshahi et al., 2015).
Fig. 5
Fig. 5
The generative model used to simulate reading. This graphical model shows the conditional dependencies of the generative model used in subsequent figures, using the same format as Fig. 1. In this model there are two hierarchical levels with three hidden states at the second level and four at the first level (hidden states and outcomes pertaining to categorical decisions and feedback have been omitted for clarity). The hidden states at the higher level correspond to the sentence or narrative – generating sequences of words at the first level – and which word the agent is currently sampling (with six alternative sentences and four words respectively). These (higher level) hidden states combine to specify the word generated at the first level (flee, feed or wait). The hidden states at the first level comprise the current word and which quadrant the agent is looking at. These hidden states combine to generate outcomes in terms of letters or icons that would be sampled if the agent looked at a particular location in the current word. In addition, two further hidden states provide a local feature context by flipping the locations vertically or horizontally. The vertical flip can be thought of in terms of font substitution (upper case versus lowercase), while the horizontal flip means a word is invariant under changes to the order of the letters (c.f., palindromes that read the same backwards as forwards). In this example, flee means that a bird is next to a cat, feed means a bird is next to some seeds and wait means seeds are above (or below) the bird. Notice that there are outcomes at both levels. At the higher level there is a (proprioceptive) outcome signalling the word currently being sampled (e.g., head position), while at the lower level there are two outcome modalities. The first (exteroceptive) outcome corresponds to the observed letter and the second (proprioceptive) outcome reports the letter location (e.g., direction of gaze in a head-centred frame of reference). Similarly, there are policies at both levels. The high-level policy determines which word the agent is currently reading, while the lower level dictates the transitions among the quadrants containing letters.
Fig. 6
Fig. 6
Simulated behavioural responses during reading: upper panel. This shows the trajectory of eye movements over four transitions at the second level that entail one or two saccadic eye movements at the first. In this trial, the subject looks at the first quadrant of the first word and sees a cat. She therefore knows immediately that the first word is flee. She then turns to the first quadrant of the second word and sees nothing. To resolve uncertainty she then looks at the fourth quadrant and again finds nothing, which means this word must be wait (because the second word of each sentence is either flee or wait – and the current word cannot be flee because the cat cannot be next to the bird). The next two saccades, on the subsequent word confirm the word feed (with the seed next to the bird sampled on the first saccade). Finally, the subject turns to the final word and discloses seeds after the second saccade. At this point, uncertainty about the sentence (sentence one versus sentence four) is resolved and the subject makes a correct categorisation – a happy story. Lower panel: this panel shows expected outcomes at the end of sampling each word. The upper row shows the final beliefs about the words under (correct) expectations about the sentence at the second level. This (first) sentence was “flee, wait, feed and wait”. At the first level, expectations about the letters under posterior beliefs about the words are shown in terms of mixtures of icons.
Fig. 7
Fig. 7
Simulated electrophysiological responses during reading: these panels show the Bayesian belief updating that underlies the behaviour and expectations reported in the previous figure. Expectations about the initial hidden state (at the first time step) at the higher (upper panel A) and lower (middle panel B) hierarchical levels are presented in raster format, where an expectation of one corresponds to black (i.e., the firing rate activity corresponds to image intensity). The horizontal axis is time over the entire trial, where each iteration corresponds roughly to 16 ms. The vertical axis corresponds to the six sentences at the higher level and the three words at the lower level. The resulting patterns of firing rate over time show a marked resemblance to delay period activity in the prefrontal cortex prior to saccades. Saccade onsets are shown with the vertical (cyan) lines. The inset on the upper right is based upon the empirical results reported in (Funahashi, 2014). The transients in the lower panel (C) are the firing rates in the upper panels filtered between 4 Hz and 32 Hz – and can be regarded as (band pass filtered) fluctuations in depolarisation. These simulated local field potentials are again remarkably similar to empirical responses. The examples shown in the inset are based on the study of perisaccadic electrophysiological responses during activation reported in (Purpura et al., 2003). The upper traces come from early visual cortex (V2), while the lower traces come from inferotemporal cortex (TE). These can be thought of as first and second level empirical responses respectively. The lower panel (D) reproduces the eye movement trajectories of the previous figure. The simulated electrophysiological responses highlighted in cyan are characterised in more detail in the next figure.
Fig. 8
Fig. 8
Simulated electrophysiological responses to violations: these simulated electrophysiological correlates focus on the perisaccadic responses around the last saccade prior to the final epoch, i.e. the cyan region highlighted in Fig. 7. The blue lines report the (filtered) expectations over peristimulus time at the first level (with one line for each of the three words), while the red lines show the evolution of expectations at the second level (with one line for each of the six sentences). Here, we repeated the simulations using the same stimuli and actions but under different prior beliefs. First, we reversed the prior expectation of a lower case by switching the informative priors on the vertical flip for, and only for, the last word. This means that the stimuli violated local expectations, producing slightly greater excursions in the dynamics of belief updating. These can be seen in slight differences between the normal\ standard response (dotted line) and the response to the surprising letter (solid lines) in the upper left panel. The ensuing difference waveform is shown on the upper right panel and looks remarkably like the classical mismatch negativity. Second, we made the inferred sentence surprising by decreasing its prior probability by a factor of eight. This global violation rendered the sampled word relatively surprising, producing a difference waveform with more protracted dynamics. Again, this is remarkably similar to empirical P300 responses seen with global violations. Finally, we combined the local and global priors to examine the interaction between local and global violations in terms of the difference in difference waveforms (these are not the differences in the difference waveforms above, which are referenced to the same normal response). The results are shown on the lower right and suggest that the effect of a global violation on the effects of a local violation (and vice versa) is largely restricted to early responses. The insert illustrates empirical event related potentials to unexpected stimuli elicited in patients with altered levels of consciousness to illustrate the form of empirical MMN and P300 responses (Fischer et al., 2000). (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Arikuni T., Kubota K. The organization of prefrontocaudate projections and their laminar origin in the macaque monkey: a retrograde study using HRP-gel. J. Comp. Neurol. 1986;244:492–510. - PubMed
    1. Barlow H. Possible principles underlying the transformations of sensory messages. In: Rosenblith W., editor. Sensory Communication. MIT Press; Cambridge, MA: 1961. pp. 217–234.
    1. Barlow H.B. Inductive inference, coding, perception, and language. Perception. 1974;3:123–134. - PubMed
    1. Bastos A.M., Usrey W.M., Adams R.A., Mangun G.R., Fries P., Friston K.J. Canonical microcircuits for predictive coding. Neuron. 2012;76:695–711. - PMC - PubMed
    1. Beal M.J. University College London; 2003. Variational Algorithms for Approximate Bayesian Inference. PhD Thesis.