Scene Construction, Visual Foraging, and Active Inference - PubMed Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2016 Jun 14:10:56.
doi: 10.3389/fncom.2016.00056. eCollection 2016.

Scene Construction, Visual Foraging, and Active Inference

M Berk Mirza  1 , Rick A Adams  2 , Christoph D Mathys  3 , Karl J Friston  1
Affiliations

Scene Construction, Visual Foraging, and Active Inference

M Berk Mirza et al. Front Comput Neurosci. .

Abstract

This paper describes an active inference scheme for visual searches and the perceptual synthesis entailed by scene construction. Active inference assumes that perception and action minimize variational free energy, where actions are selected to minimize the free energy expected in the future. This assumption generalizes risk-sensitive control and expected utility theory to include epistemic value; namely, the value (or salience) of information inherent in resolving uncertainty about the causes of ambiguous cues or outcomes. Here, we apply active inference to saccadic searches of a visual scene. We consider the (difficult) problem of categorizing a scene, based on the spatial relationship among visual objects where, crucially, visual cues are sampled myopically through a sequence of saccadic eye movements. This means that evidence for competing hypotheses about the scene has to be accumulated sequentially, calling upon both prediction (planning) and postdiction (memory). Our aim is to highlight some simple but fundamental aspects of the requisite functional anatomy; namely, the link between approximate Bayesian inference under mean field assumptions and functional segregation in the visual cortex. This link rests upon the (neurobiologically plausible) process theory that accompanies the normative formulation of active inference for Markov decision processes. In future work, we hope to use this scheme to model empirical saccadic searches and identify the prior beliefs that underwrite intersubject variability in the way people forage for information in visual scenes (e.g., in schizophrenia).

Keywords: Bayesian inference; active inference; epistemic value; free energy; information gain; salience; scene construction; visual search.

PubMed Disclaimer

Figures

Figure 1
Figure 1
Formal specification of the generative model and (approximate) posterior. (A) These equations specify the form of the (Markovian) generative model used in this paper. A generative model is essentially a specification of the joint probability of outcomes or consequences and their (latent or hidden) causes. Usually, this model is expressed in terms of a likelihood (the probability of consequences given causes) and priors over the causes. When a prior depends upon a random variable it is called an empirical prior. Here, the generative model specifies the mapping between hidden states and observable outcomes in terms of the likelihood. The priors in this instance pertain to transitions among hidden states that depend upon action, where actions are determined probabilistically in terms of policies (sequences of actions). The key aspect of this generative model is that, a priori, policies are more probable if they minimize the (path integral of) expected free energy G. Bayesian model inversion refers to the inverse mapping from consequences to causes; i.e., estimating the hidden states and other variables that cause outcomes. (B) In variational Bayesian inversion, one has to specify the form of an approximate posterior distribution, which is provided on the right panel. This particular form uses a mean field approximation, in which posterior beliefs are approximated by the product of marginals or factors. Here, a mean field approximation is applied both to posterior beliefs at different points in time and different sorts of hidden states. See the main text and Table 1 for more detailed explanation of the variables.
Figure 2
Figure 2
Graphical model corresponding to the generative model. (A) The left panel shows the conditional dependencies implied by the generative model of previous figure. Here, the variables in white circles constitute (hyper) priors, while the blue circles denote random variables. This format shows how outcomes are generated from hidden states that evolve according to probabilistic transitions, which depend on policies. The probability of a particular policy being selected depends upon expected free energy and a precision or inverse temperature. (B) The right panels show an example of different hidden states and outcomes modalities. This particular example will be used later to model perceptual categorization in terms of three scenarios or scenes (flee, feed, or wait). The two outcome modalities effectively report what is seen and where it is seen. See the main text for a more detailed explanation.
Figure 3
Figure 3
Schematic overview of the belief updates describing active inference: (A) The left panel lists the belief updates mediating, perception, policy selection, precision, and action selection; (B) while the right panel assigns the quantities that are updated (sufficient statistics or expectations) to various brain areas. The implicit attribution should not be taken too seriously but serves to illustrate the functional anatomy implied by the form of the belief updates. Here, we have assigned observed outcomes to visual representations in the occipital cortex; with exteroceptive (what) modalities entering a ventral stream and proprioceptive (where) modalities originating a dorsal stream. Hidden states encoding context have been associated with the hippocampal formation, while the remaining states encoding sampling location and spatial invariance have been assigned to the parietal cortex. The evaluation of policies, in terms of their (expected) free energy, has been placed in the ventral prefrontal cortex. Expectations about policies per se and the precision of these beliefs have been associated with striatal and ventral tegmental areas to indicate a putative role for dopamine in encoding precision. Finally, beliefs about policies are used to create Bayesian model averages of future outcomes (in the frontal eye fields)—that are fulfilled by action, via the deep layers of the superior colliculus. The arrows denote message passing among the sufficient statistics of each factor or marginal. Please see the text and Table 1 for an explanation of the equations and variables. In this paper, the hat notation denotes a natural logarithm; i.e., o⌢=ln o.
Figure 4
Figure 4
Simulated visual search: (A) This panel shows the expectations about hidden states and the expectations of actions are shown in (B) (upper middle), producing the search trajectory in (C)—after completion of the last saccadic movement. Expectations are shown in image format with black representing 100% probability. For the hidden states each of the four factors or marginals are shown separately, with the true states indicated by cyan dots. Here, there are five saccades and the agent represents hidden states generating six outcomes (the initial state and five subsequent outcomes). The results are shown after completion of the last saccadic, which means that, retrospectively, the agent believes it started in a flee context, with no horizontal or vertical reflection. The sequence of sampling locations indicates that the agent first interrogated the lower right quadrant and then emitted saccades to the upper locations to correctly infer the scene—and make the correct choice (indicated by the red label). The lower panel (D) illustrates the beliefs about context during the first four saccades. Initially, the agent is very uncertain about the constituents of each peripheral location; however, this uncertainty is progressively resolved through epistemic foraging, based upon the cues that are elicited by saccades (shown in the central location). The blue dots indicate the sampling location after each saccade.
Figure 5
Figure 5
Simulated electrophysiological responses: this figure reports the belief updating behind the behavior shown in the previous figure. (A) The upper left panel shows the activity (firing rate) of units encoding the context or scene in image (raster) format, over the six intervals between saccades. These responses are organized such that the upper rows encode the probability of alternative states in the first epoch, with subsequent epochs in lower rows. (B) The upper right panel plots the same information to illustrate the evidence accumulation and the resulting disambiguation of context. (C) The simulated local field potentials for these units (i.e., the rate of change of neuronal firing) are shown in the middle left panel. (D) The middle right panel shows average local field potential over all units before (dotted line) and after (solid line) bandpass filtering at 4 Hz, superimposed upon its time frequency decomposition. (E) The lower panel illustrates simulated dopamine responses in terms of a mixture of precision and its rate of change.
Figure 6
Figure 6
Simulated responses over 32 trials: this figure reports the behavioral and (simulated) physiological responses during 32 successive trials. The scenes in these 32 trials were specified via randomly selected hidden states of the world. (A) The first panel shows the hidden states of the scene (as colored circles) and the selected action (i.e., the sampled location) on the last saccade. The y-axis on this panel shows two quantities. The selected action is shown using black bars. The agent can saccade to locations one to eight, where the locations six to eight correspond to the choice locations the agent uses to report the scene category. The true hidden states are shown with colored circles. These specify the objects in the scene and their locations (in terms of the context and spatial transformations). The second row of cyan dots indicates that the agent always starts exploring a scene from the central fixation point. Individual rows in the y-axis indicate the sampled locations according to the following: Fix, Fixation; U. Left, Upper left; L. Left, Lower Left; U. Right, Upper Right; L. Right, Lower Right; and Ch. Flee, Choose Flee; Ch. Feed, Choose Feed; and Ch. Wait, Choose Wait. (B) The second panel reports the final outcomes (encoded by colored circles) and performance measures in terms of preferred outcomes (utility of observed outcomes), summed over time (black bars) and standardized reaction times (cyan dots). The final outcomes are shown for the sample location (upper row of dots) and outcome (lower row of dots): yellow means the agent made a right choice. (C) The third panel shows a succession of simulated event related potentials following each outcome. These are taken to be the rate of change of neuronal activity, encoding the expected probability of hidden states encoding context (i.e., simulated hippocampal activity).
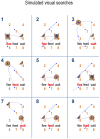
Figure 7
Figure 7
Sequences of saccades: this figure illustrates the behavior for the first nine trials shown in the previous figure using the same format as Figure 4 (upper right panel). The numbers on the top left in each cell show the trial number. With the exception of the third trial, the agent is able to recognize or categorize the scene after a small number of epistemically efficient saccades.
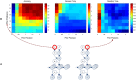
Figure 8
Figure 8
Performance and priors: this figure illustrates the average performance over 300 trials. (A) The insert (lower panel) shows the prior parameters that were varied; namely, prior preference and precision. These parameters are varied over eight levels. (B) For each combination, the accuracy, decision and reaction time were evaluated using simulations (upper row). The accuracy is expressed as the percentage of correct trials (defined as a correct choice in the absence of a proceeding or subsequent incorrect choice). Decision time is defined in terms of the number of saccades until a (correct or incorrect) decision. Reaction time or the interval between saccades is measured in seconds and corresponds to the actual computation time during the simulations.
See this image and copyright information in PMC

Similar articles

  • Active inference and learning.
    Friston K, FitzGerald T, Rigoli F, Schwartenbeck P, O Doherty J, Pezzulo G. Friston K, et al. Neurosci Biobehav Rev. 2016 Sep;68:862-879. doi: 10.1016/j.neubiorev.2016.06.022. Epub 2016 Jun 29. Neurosci Biobehav Rev. 2016. PMID: 27375276 Free PMC article. Review.
  • Deep Active Inference and Scene Construction.
    Heins RC, Mirza MB, Parr T, Friston K, Kagan I, Pooresmaeili A. Heins RC, et al. Front Artif Intell. 2020 Oct 28;3:509354. doi: 10.3389/frai.2020.509354. eCollection 2020. Front Artif Intell. 2020. PMID: 33733195 Free PMC article.
  • Human visual exploration reduces uncertainty about the sensed world.
    Mirza MB, Adams RA, Mathys C, Friston KJ. Mirza MB, et al. PLoS One. 2018 Jan 5;13(1):e0190429. doi: 10.1371/journal.pone.0190429. eCollection 2018. PLoS One. 2018. PMID: 29304087 Free PMC article.
  • Perceptions as hypotheses: saccades as experiments.
    Friston K, Adams RA, Perrinet L, Breakspear M. Friston K, et al. Front Psychol. 2012 May 28;3:151. doi: 10.3389/fpsyg.2012.00151. eCollection 2012. Front Psychol. 2012. PMID: 22654776 Free PMC article.
  • The active construction of the visual world.
    Parr T, Friston KJ. Parr T, et al. Neuropsychologia. 2017 Sep;104:92-101. doi: 10.1016/j.neuropsychologia.2017.08.003. Epub 2017 Aug 3. Neuropsychologia. 2017. PMID: 28782543 Free PMC article. Review.
See all similar articles

Cited by

See all "Cited by" articles

References

    1. Andreopoulos A., Tsotsos J. (2013). A computational learning theory of active object recognition under uncertainty. Int. J. Comput. Vis. 101, 95–142. 10.1007/s11263-012-0551-6 - DOI
    1. Barlow H. (1961). Possible principles underlying the transformations of sensory messages, in Sensory Communication, ed Rosenblith W. (Cambridge, MA: MIT Press; ), 217–234.
    1. Beal M. J. (2003). Variational Algorithms for Approximate Bayesian Inference. Ph.D. thesis, University College London.
    1. Beedie S. A., Benson P. J., St Clair D. M. (2011). Atypical scanpaths in schizophrenia: evidence of a trait- or state-dependent phenomenon? J. Psychiatry Neurosci. 36, 150–164. 10.1503/jpn.090169 - DOI - PMC - PubMed
    1. Bellman R. (1952). On the theory of dynamic programming. Proc. Natl. Acad. Sci. U.S.A 38, 716–719. - PMC - PubMed

LinkOut - more resources