Spike-Based Bayesian-Hebbian Learning of Temporal Sequences - PubMed Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2016 May 23;12(5):e1004954.
doi: 10.1371/journal.pcbi.1004954. eCollection 2016 May.

Spike-Based Bayesian-Hebbian Learning of Temporal Sequences

Philip J Tully  1   2   3 , Henrik Lindén  1   2   4 , Matthias H Hennig  3 , Anders Lansner  1   2   5
Affiliations

Spike-Based Bayesian-Hebbian Learning of Temporal Sequences

Philip J Tully et al. PLoS Comput Biol. .

Abstract

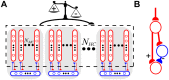
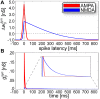
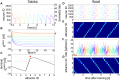
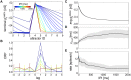
Many cognitive and motor functions are enabled by the temporal representation and processing of stimuli, but it remains an open issue how neocortical microcircuits can reliably encode and replay such sequences of information. To better understand this, a modular attractor memory network is proposed in which meta-stable sequential attractor transitions are learned through changes to synaptic weights and intrinsic excitabilities via the spike-based Bayesian Confidence Propagation Neural Network (BCPNN) learning rule. We find that the formation of distributed memories, embodied by increased periods of firing in pools of excitatory neurons, together with asymmetrical associations between these distinct network states, can be acquired through plasticity. The model's feasibility is demonstrated using simulations of adaptive exponential integrate-and-fire model neurons (AdEx). We show that the learning and speed of sequence replay depends on a confluence of biophysically relevant parameters including stimulus duration, level of background noise, ratio of synaptic currents, and strengths of short-term depression and adaptation. Moreover, sequence elements are shown to flexibly participate multiple times in the sequence, suggesting that spiking attractor networks of this type can support an efficient combinatorial code. The model provides a principled approach towards understanding how multiple interacting plasticity mechanisms can coordinate hetero-associative learning in unison.

PubMed Disclaimer

Conflict of interest statement

The authors have declared that no competing interests exist.

Figures

Fig 1
Fig 1. Organization of a neocortical microcircuit.
(A) The WTA hypercolumns (shaded gray areas) consisted of excitatory neurons (red circles) belonging to minicolumns (red ovals) that innervated (red arrows) local populations (blue ovals) of basket cells (blue circles), which provided inhibitory feedback (blue arrows). Nonspecific BCPNN synapses (black arrow) were recurrently connected amongst all excitatory neurons (black dotted box), with learned weights (scale) determined by pre- and postsynaptic spike activity. Semicircular arrowheads indicate the postsynaptic target. (B) Schematic of a polysynaptic subcircuit that elicited a net excitatory effect on the postsynaptic neuron when the BCPNN weight was positive (+ pathway), while a negative BCPNN weight can be thought of as being converted to inhibition via excitation of a local inhibitory interneuron (− pathway).
Fig 2
Fig 2. Matching learning and synaptic time constants for AMPA and NMDA.
(A) Absolute change in peak synaptic amplitude after 100 pre- and postsynaptic events at 1 Hz, where spike latency > 0 denotes a pre before post pairing. (B) Postsynaptic conductances elicited by EPSPs via AMPA and NMDA receptors display similar time courses of activation to their corresponding learning window widths from (A). The inset provides a zoomed view of the area contained within the dotted gray lines.
Fig 3
Fig 3. Learning spontaneously wandering attractor states.
(A) Alternate network schematic with hypercolumns (large black circles), along with their member minicolumns (smaller colored circles) and local basket cell populations (centered gray circles). Minicolumns with the same color across different hypercolumns belong to the same pattern; these color indicators are used in the following subfigures. (B) Rastergram (10x downsampled, henceforth) and superimposed firing rates (10 ms bins averaged per pattern, henceforth) associated with the first training epoch. (C) Progression of the ‘print-now’ κ signal whose brief activations are synchronized with the incoming stimuli from (B). (D) Development of Iβj during training and averaged over 50 randomly selected neurons per pattern. The period of time shown in (B, C) can be discerned as * for reference. (E) Development of average gijAMPA during training that project from neurons belonging to the first stimulated (i.e. red) pattern, with colors denoting target postsynaptic neuron pattern. (F) Same as (E), except showing gijNMDA development during training. (G) Rastergram snapshot of excitatory neurons during recall. (H) Relative average firing rates based on (G) and sorted by attractor membership. Each row represents the firing rate of one attractor. (I) Average firing rate of the attractors displaying the random progression of the network through state space. Arrows highlight the ground state, which are competitive phases lacking a dominantly active attractor. (J) Evolution of the adaptation current Iw for a single neuron whose activity builds up and attenuates as it enters and exits attractor states. (K) Evolution of the same neuron’s dynamic AMPA strength due to short-term depression, whose postsynaptic target resides within the same attractor.
Fig 4
Fig 4. Learning sequential attractor states.
(A) Rastergram and firing rates associated with the first out of 50 epochs of training. (B) Average gijNMDA during training emanating from neurons belonging to the first stimulated pattern as in Fig 3E (indicated with red arrow, colors denote target postsynaptic neuron pattern). Contrast the weight trajectories between patterns with Fig 3F. (C) Average gijNMDA after training that depicts an asymmetrical terminal weight profile. As in (B), the red arrow indicates the presynaptic perspective taken from the first stimulated pattern, which is aligned here at index 4. (D) Rastergram snapshot of excitatory neurons during recall. (E) Relative average firing rates based on (D) and sorted by attractor membership as in Fig 3H. The sequence is chronologically ordered according to the trained patterns from (A). (F) Average firing rate of attractors displaying the sequential progression of the network through state space. (G) Resulting recall after training the network by exchanging τziNMDA for τzjNMDA showing the reverse traversal of attractor states from (D-F). Firing rates here and in (E) are coded according to the colorbar from Fig 3H.
Fig 5
Fig 5. The temporal structure of neural recall dynamics reflects the temporal interval used during training.
(A) Average gijNMDA after training as in Fig 4C (reproduced here by the 0 ms line) except now depicting terminal weight profiles for many differently trained networks with IPIs varying between 0 and 2000 ms. (B) CRP curves calculated for networks with representative IPIs = 0, 500, 1000, 1500 and 2000 ms after 1 minute of recall, with colors corresponding to (A). Increasing IPIs flattened the CRP curve, promoting attractor transition distribution evenness. Error bars reflect standard deviations. (C) Average strength of gijNMDA taken across entire networks after training for different IPIs, where the number of NMDA synapses in these separate networks was constant. (D) Average dwell times μdwell measured during 1 minute recall periods for entire networks trained with different IPIs. Shaded areas denote standard deviations here and in (E). (E) Average neural firing rates for attractors with dwell times corresponding to those measured in (D).
Fig 6
Fig 6. Upkeep of stable sequential state switching during recall is permitted by the interplay of excitation and inhibition in a single neuron.
(A) Recorded Vm of a randomly chosen single cell whose period of increased tendency for being suprathreshold coincided with its brief engagement within an attractor. The red dotted line represents the membrane voltage threshold Vt for reference, and the shaded area represents a detected attractor state that is reproduced in B-D. (B) The same cell’s net NMDA current, which combined positive and negative afferent BCPNN weights. (C) The same cell’s net AMPA current, which combined positive and negative afferent BCPNN weights. (D) The same cell’s GABA current originating from local basket cell inhibition.
Fig 7
Fig 7. Rank ordered ramps of Vm depolariziations forecast the serial position of upcoming attractors during cue-triggered recall of a temporal sequence.
(A) A cue (red star) presented 1 second into recall resonates through the trained network. (B) Activity levels based on (A) and sorted by attractor membership as in Figs 3H and 4D. (C) Average Vm (1 ms bins) taken for all excitatory cells in the network and smoothed per attractor index by a moving average with 200 ms window length. Truncated Vm values at the beginning and end are artifacts of the moving average procedure. In this example both before and after the cued sequence, patterns spontaneously but weakly activated, which could occur randomly due to the sensitivity of the system. Black arrows represent time periods occurring after the midpoint of the cue initially and after the midpoint of each attractor thereafter, during which the average Vm of the upcoming attractors are ranked according to their relative serial order within the sequence.
Fig 8
Fig 8. Dependence of temporal sequence speed on the duration of conditioning stimuli.
(A) Average gijNMDA after training as in Fig 4C (reproduced here by the 100 ms line). (B) Speeds computed for the networks from (A) after 1 minute of recall. The dotted gray line represents a linear relationship between training and recall speeds (compression factor = 1), tstim used previously can be discerned as * for reference, “attrs” abbreviates attractors and the shaded areas denotes the standard deviation.
Fig 9
Fig 9. Multiparametric intrinsic determinants of temporal sequence speed.
Univariate effects on recall speed are quantified by modulating (A) the rate of background excitation, (B) the AMPA/NMDA ratio, (C) the magnitude of neural adaptation, (D) the magnitude of short-term depression, (E) the time constant of neural adaptation and (F) the time constant of short-term depression. Simulations using the parameters from Fig 8B were reproduced in A-F in red for comparison. The dotted gray line represents a linear relationship between training and recall speeds (compression factor = 1, see Eq 12), “attrs” abbreviates attractors and shaded areas denote standard deviations.
Fig 10
Fig 10. Characterization of speed changes.
(A) Compression factor ranges measured for trained speeds of 2 patterns/second achieved by altering one parameter at a time and keeping all others constant. Horizontal bars denote compression factor cutoffs that were maximally allowable without violating edit distance tolerance levels, and the gray dotted line indicates a compression factor of 1. A second value does not exist for training speed since it was held at 2 patterns/second. (B) Cloud of points summarizing recall speeds and their corresponding firing rates from Fig 9. The linear regression line is displayed in red where r2 represents the square of the Pearson product-moment correlation coefficient of the two variables. (C) Correlation coefficients for individual mechanisms.
Fig 11
Fig 11. Cue-triggered overlapping sequence completion and disambiguation.
(A) Schematic of sequential training patterns used to demonstrate completion. Roman numerals label uniquely trained subsequences that were alternatingly presented to the network, and the gray box highlights overlapping subsequence patterns. (B) Terminal average gijNMDA matrix resulting from (A). White Roman numerals identify regions of the weight matrix corresponding to learned connections between the non-overlapping subsequences of (A), which were reciprocally inhibiting. Black Roman numerals identify the crucial associations used for bridging the two subsequences together. (C) A cue (red star) presented to the first pattern 1 second into recall resonates through the network. (D) Schematic of the training pattern as in (A) demonstrating the problem of sequence disambiguation. (E) Terminal average gijNMDA matrix resulting from (D) and white Roman numerals as in (B). Here, black Roman numerals identify the crucial associations for bridging each individual subsequence together despite their shared patterns, which each form indistinguishable average connection strengths towards each branch of the fork as emphasized by the equivalent matrix cells contained within the dotted outlines. (F) Two separate cues (red and blue stars) presented 8 seconds apart each resonate through their corresponding subnetworks.
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Averbeck BB, Chafee MV, Crowe DA, Georgopoulos AP (2002) Parallel processing of serial movements in prefrontal cortex. Proc Natl Acad Sci USA 99: 13172–13177. - PMC - PubMed
    1. Nakajima T, Hosaka R, Mushiake H, Tanji J (2009) Covert Representation of Second-Next Movement in the Pre-Supplementary Motor Area of Monkeys. Journal of Neurophysiology 101: 1883–1889. 10.1152/jn.90636.2008 - DOI - PubMed
    1. Mattia M, Pani P, Mirabella G, Costa S, Giudice PD, et al. (2013) Heterogeneous Attractor Cell Assemblies for Motor Planning in Premotor Cortex. The Journal of Neuroscience 33: 11155–11168. 10.1523/JNEUROSCI.4664-12.2013 - DOI - PMC - PubMed
    1. Jones LM, Fontanini A, Sadacca BF, Miller P, Katz DB (2007) Natural stimuli evoke dynamic sequences of states in sensory cortical ensembles. Proc Natl Acad Sci USA 104: 18772–18777. - PMC - PubMed
    1. Crowe DA, Averbeck BB, Chafee MV (2010) Rapid Sequences of Population Activity Patterns Dynamically Encode Task-Critical Spatial Information in Parietal Cortex. Journal of Neuroscience 30: 11640–11653. 10.1523/JNEUROSCI.0954-10.2010 - DOI - PMC - PubMed

Publication types

Substances