Dopamine, reward learning, and active inference - PubMed Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2015 Nov 4:9:136.
doi: 10.3389/fncom.2015.00136. eCollection 2015.

Dopamine, reward learning, and active inference

Thomas H B FitzGerald  1 , Raymond J Dolan  1 , Karl Friston  2
Affiliations

Dopamine, reward learning, and active inference

Thomas H B FitzGerald et al. Front Comput Neurosci. .

Abstract

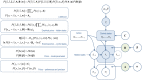
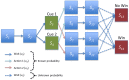
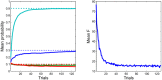
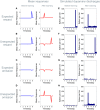
Temporal difference learning models propose phasic dopamine signaling encodes reward prediction errors that drive learning. This is supported by studies where optogenetic stimulation of dopamine neurons can stand in lieu of actual reward. Nevertheless, a large body of data also shows that dopamine is not necessary for learning, and that dopamine depletion primarily affects task performance. We offer a resolution to this paradox based on an hypothesis that dopamine encodes the precision of beliefs about alternative actions, and thus controls the outcome-sensitivity of behavior. We extend an active inference scheme for solving Markov decision processes to include learning, and show that simulated dopamine dynamics strongly resemble those actually observed during instrumental conditioning. Furthermore, simulated dopamine depletion impairs performance but spares learning, while simulated excitation of dopamine neurons drives reward learning, through aberrant inference about outcome states. Our formal approach provides a novel and parsimonious reconciliation of apparently divergent experimental findings.

Keywords: active inference; dopamine; incentive salience; instrumental conditioning; learning; reward; reward learning; variational inference.

PubMed Disclaimer

Figures

Figure 1
Figure 1
Active inference model. This illustrates dependencies between the variables in the augmented generative model of behavior (for further details see Friston et al., 2013). Left: these equations specify the generative model in terms of the joint probability over observations õ, hidden states s~, control states ũ, the precision of beliefs about control states γ~, and the parameters encoded by the matrices that determine the mapping between hidden states A and the transition probabilities between hidden states B(u). The form of these equations rests upon Markovian assumptions about controlled state transitions. Right: Bayesian graph showing the dependencies among hidden states and how they depend upon past and future control states. Sequences of future control states (policies) depend upon the current state, because policy selection depends upon the divergence between distributions over the final state that are, and are not, conditioned on the current state, together with the precision of beliefs about control states. Observed outcomes depend only on the hidden states at any given time. Given this generative model, an agent can make inferences about observed outcomes using variational Bayes (Beal, 2003). The same variational scheme can also learn the model parameters encoded by the A and B matrices. States and parameters are treated identically, except for the key distinction that because parameters are time-invariant, information about them can be accumulated over time. (States that are inferred upon are indicated in blue, parameters that are learnt in green).
Figure 2
Figure 2
Structure of instrumental conditioning task. In each trial the agent first proceeds through two initial pre-cue states. One of two cues is then presented with equal probability, and the agent takes one of two actions. The agent then waits for two epochs or delayed periods, where each pair of hidden states corresponds to a particular cue-outcome combination. Finally, the agent moves probabilistically either to a win or no win outcome. Agents had strong and accurate beliefs about all transition probabilities except for the transitions to the final outcomes outcome, which had to be learnt.
Figure 3
Figure 3
Schematic depicting the relationships among temporal difference learning, incentive salience, and precision hypotheses; in terms of explaining the phenomena we consider in this paper. The temporal difference learning hypothesis correctly predicts both reward prediction error-like phasic dopamine responses and the fact that dopaminergic stimulation is sufficient to establish preference learning. However, it does not predict either a direct effect of dopamine on action selection or the fact that dopamine is not necessary for preference learning. The incentive salience hypothesis, by contrast, predicts the effect of dopamine on action selection, and that it is not needed for learning, but struggles to explain the other two phenomena. The precision hypothesis, by contrast, accounts for all four. (This figure is intended to be illustrative rather than comprehensive, and we acknowledge that there are a number of key phenomena that are currently not well-explained by the precision hypothesis, as described in the Discussion).
Figure 4
Figure 4
Learning performance. Left: the agent rapidly and accurately learns the unknown transition probabilities. (Dotted lines: actual values, continuous lines: estimated values) Right: this is accompanied by a progressive reduction in the variational free energy, confirming the agent has improved its model of the task. (Data are averaged across 256 repetitions of 128 simulated trials).
Figure 5
Figure 5
Learning induced changes in the dynamics of the dopamine signal. The panels on the left hand side of the figure (A–D) show simulated dopaminergic dynamics at a population level, whilst those on the right hand side (E–H) show simulated activity in dopaminergic neurons assuming that an expected precision of one is encoded by four spikes per bin with a background firing rate of four spikes per bin. (Firing rates are simulated using a Poisson process, averaged over 64 simulated trials) Here we illustrate simulated dopamine responses for four trial types, those on which a cue predicting a high likelihood of reward is presented and a reward is received (“expected reward,” A,E), or omitted (“unexpected omission,” D,H), and those on which a cue predicting a low likelihood of reward is presented, and a reward is received (“unexpected reward,” B,F) or omitted (“expected omission,” C,G). (For details of the simulations, see main text) Before learning (blue), no expectations have been established, and dopamine responses to reward-predicting stimuli are absent (time point three), but clear responses are shown to rewarding outcomes (time point six, top two rows). (The small dip when reward is omitted (bottom two rows) reflects the agent's initial belief that it will receive reward with a small but non-zero probability at the end of each trial). After learning (red), by contrast, clear positive responses are seen to the high reward cue (top and bottom rows) with a dip accompanying the presentation of the low-reward cue (middle rows). Learning also induces changes in the responses to outcomes, such that when reward is strongly expected responses to rewarding outcomes are strongly attenuated (A,E), and those to reward omissions increased (D,H). This mirrors the “reward prediction error” pattern of responding widely reported to occur in dopamine neurons during conditioning.
Figure 6
Figure 6
Evolution of dopamine responses and effects of dopamine on behavior. (A) Transfer of simulated dopamine responses from outcome to cue during learning. Responses to rewarding outcomes (epoch or update six) diminish over the course of learning, whilst those to the reward-predicting cue (epoch three) increase in magnitude. Unlike in many temporal difference learning models, the transfer of responses is direct (i.e., not mediated by dopamine responses at intervening time points). This constitutes a clear and testable prediction of our model, when compared with temporal difference learning accounts of phasic dopamine responses. (B) The effects of simulated dopamine depletion on task performance. Fixing expected precision to a low value (0.1) appears to prevent learning, as indexed by the proportion of correct responses selected by the agent (blue line, first 32 trials). However, learning does in fact occur, but is simply masked by the effects of reduced precision on choice behavior. This is revealed after restoration of normal function (trial 33 onwards), at which point performance becomes comparable to that of a non-lesioned agent. (Figure shows choice behavior averaged across 256 simulated sessions). (C) Parameter learning during dopamine depletion. The agent is able to accurately learn unknown transition probabilities as during normal function (Figure 4), even though this is masked by the effects of dopamine on action selection as shown in (B) (Dotted lines: actual values, continuous lines: estimated values).
Figure 7
Figure 7
The effect of simulated stimulation of the dopaminergic midbrain at outcome presentation. On both trials, the agent was presented with an identical series of observations (A), corresponding to observing cue one and a no win outcome. In one case (left column) the agent was allowed to infer precision as usual, leading to a small dip in precision at outcome time (B) and the correct inference that it had reached a no win outcome state (C). In the other trial (right panel), midbrain stimulation was simulated by fixing expected precision at a high value at outcome time(γ6 = 16) (B). This leads, via the effect of precision on state estimation (see update Equation 23 and Friston et al., 2013) to an incorrect inference that it has reached a win outcome state (C). (D) shows the effect on inference of stimulation with values varying between 8 and 16. The posterior probability of being in a win outcome state (green) increases as stimulation strength increases, whilst the posterior probability of being in a no win outcome state (blue) falls correspondingly.
Figure 8
Figure 8
The effect of simulated stimulation of the dopaminergic midbrain on learning. The agent was presented with a single cue, with task contingencies such that making response one (blue) never led to reward, whilst response two (green) led to reward with probability 0.5. In the stimulation condition (bold lines), selection of response one was always followed by simulated stimulation at outcome time (γ6 = 16). In the control condition (dashed lines), no stimulation occurred. Stimulation was sufficient to induce a reversal in preference, with response one selected more often, even though it was never rewarded. This replicates the findings of recent optogenetic stimulation studies, even though stimulation only affects inference directly, rather than learning. (Choice behavior averaged over 256 repetitions of a 48 trial session).
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Abbott L. F., Nelson S. B. (2000). Synaptic plasticity: taming the beast. Nat. Neurosci. 3, 1178–1183. 10.1038/81453 - DOI - PubMed
    1. Adamantidis A. R., Tsai H.-C., Boutrel B., Zhang F., Stuber G. D., Budygin E. A., et al. . (2011). Optogenetic interrogation of dopaminergic modulation of the multiple phases of reward-seeking behavior. J. Neurosci. 31, 10829–10835. 10.1523/JNEUROSCI.2246-11.2011 - DOI - PMC - PubMed
    1. Adams R. A., Perrinet L. U., Friston K. (2012). Smooth pursuit and visual occlusion: active inference and oculomotor control in schizophrenia. PLoS ONE 7:e47502. 10.1371/journal.pone.0047502 - DOI - PMC - PubMed
    1. Adams R. A., Stephan K. E., Brown H. R., Frith C. D., Friston K. J. (2013). The computational anatomy of psychosis. Front. psychiatry 4:47. 10.3389/fpsyt.2013.00047 - DOI - PMC - PubMed
    1. Beal M. J. (2003). Variational Algorithms for Approximate Bayesian Inference. Ph.D. Thesis, University College London.

LinkOut - more resources