An analytic, Fourier domain description of shear wave propagation in a viscoelastic medium using asymmetric Gaussian sources - PubMed Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2015 Aug;138(2):1012-22.
doi: 10.1121/1.4927492.

An analytic, Fourier domain description of shear wave propagation in a viscoelastic medium using asymmetric Gaussian sources

Ned C Rouze  1 , Mark L Palmeri  1 , Kathryn R Nightingale  1
Affiliations

An analytic, Fourier domain description of shear wave propagation in a viscoelastic medium using asymmetric Gaussian sources

Ned C Rouze et al. J Acoust Soc Am. 2015 Aug.

Abstract

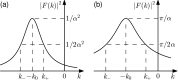
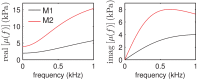
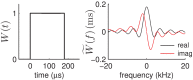
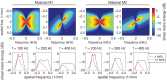
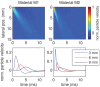
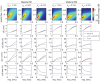
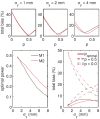
Recent measurements of shear wave propagation in viscoelastic materials have been analyzed by constructing the two-dimensional Fourier transform (2D-FT) of the spatial-temporal shear wave signal and using an analysis procedure derived under the assumption the wave is described as a plane wave, or as the asymptotic form of a wave expanding radially from a cylindrically symmetric source. This study presents an exact, analytic expression for the 2D-FT description of shear wave propagation in viscoelastic materials following asymmetric Gaussian excitations and uses this expression to evaluate the bias in 2D-FT measurements obtained using the plane or cylindrical wave assumptions. A wide range of biases are observed depending on specific values of frequency, aspect ratio R of the source asymmetry, and material properties. These biases can be reduced significantly by weighting the shear wave signal in the spatial domain to correct for the geometric spreading of the shear wavefront using a factor of x(p). The optimal weighting power p is found to be near the theoretical value of 0.5 for the case of a cylindrical source with R = 1, and decreases for asymmetric sources with R > 1.

PubMed Disclaimer

Figures

FIG. 1.
FIG. 1.
Plots of the functions (a) |F(k)|2=1/[(k+k0)2+α2] from Eq. (12) and (b) |F(k)|2=π/(k+k0)2+α2 from Eq. (19). For both cases, the maximum signal occurs at kmax = −k0 so that the phase velocity c = ω0/k0 is given by c = −ω0/kmax as in Eq. (13). For (a), the half-maximum value of 1/2α2 occurs at k ± = −k0 ± α so that FWHM = 2α as in Eq. (14). For (b), the half-maximum value of π/2α occurs at k±=−k0±3α so that FWHM=23α as in Eq. (20).
FIG. 2.
FIG. 2.
Real (left) and imaginary (right) parts of the shear modulus μ(f) calculated from Eq. (41) for materials M1 and M2 in Table I.
FIG. 3.
FIG. 3.
Excitation window W(t) (left) and the real and imaginary parts of its Fourier transform W˜(f) (right) from Eq. (42) for the case of an excitation duration T = 180 μs.
FIG. 4.
FIG. 4.
Examples of 2D-FT signals calculated for materials M1 (left side) and M2 (right side) from Table I with Gaussian excitation widths of σx = 1 mm and σy = 2 mm. For each material, the top left 2D-FT image shows |V(x)(k,ω)|2 calculated using Eqs. (39) and (36) for shear wave propagation observed along both the +x and −x axes, and the top right 2D-FT image shows |V(+x)(k,ω)|2 obtained by applying Eq. (34) for shear waves observed only along the +x axis. These signals are normalized by the maximum |V(x)(k,ω)|2 signal at a frequency of 100 Hz. The bottom row shows profiles from both of the 2D-FT images for frequencies of f = 100 Hz, f = 250 Hz, and f = 400 Hz.
FIG. 5.
FIG. 5.
Particle velocity signals v(x,t) calculated using Eq. (43) for shear wave propagation observed along the +x axis in materials M1 (left) and M2 (right) following excitations with Gaussian widths of σx = 1 mm and σy = 2 mm. These signals have been normalized by the maximum value of v(x, t) at a lateral position of x = 0 mm. The bottom plots show the normalized particle velocity signals as a function of time for x = 3 mm, x = 6 mm, and x = 9 mm.
FIG. 6.
FIG. 6.
Results obtained using the 2D-FT analysis of shear wave propagation in materials M1 and M2 from Table I for Gaussian excitation widths σx = 1 mm and σy = 1 mm, σy = 2 mm, and σy = 4 mm. The top row shows 2D-FT data calculated using Eqs. (39), (36), (34), and normalized as shown in Fig. 4. The second row shows the true phase velocity c(f) (red) calculated using Eq. (5) and measured using Eq. (13) from unweighted 2D-FT data (black) and x weighted 2D-FT data (blue) calculated using Eq. (35). The third row shows percentage biases of the measured c(f) relative to the true values. The fourth row shows true values of shear attenuation α(f) (red) calculated using Eq. (6) and measured values determined using Eq. (14) from unweighted 2D-FT data (black) and x weighted 2D-FT data (blue). The fifth row shows the percentage biases of the measured α(f) relative to the true values.
FIG. 7.
FIG. 7.
Results obtained using a weighting factor of the form xp with a variable power p in Eq. (35). The top row shows the total bias calculated as described in Sec. V for materials M1 and M2 from Table I and Gaussian sources with σx = 1 mm and σy = 1 mm (left), σy = 2 mm (center), and σy = 4 mm (right). The bottom left plot shows the optimal power corresponding to the minimum total bias plotted as a function of σy. The bottom right plot shows the total bias achieved using the weighting function with optimal power (solid lines) and also the total bias obtained using x (i.e., p = 0.5) weighted 2D-FT data (dashed lines) and unweighted (i.e., p = 0) 2D-FT data (dotted-dashed lines).
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Sarvazyan A. P., Rudenko O. V., Swanson S. D., Fowlkes J. B., and Emelianov S. Y., “ Shear wave elasticity imaging: A new ultrasonic technology of medical diagnostics,” Ultrasound Med. Biol. 24, 1419–1435 (1998).10.1016/S0301-5629(98)00110-0 - DOI - PubMed
    1. Graff K. F., Wave Motion in Elastic Solids ( Dover, Mineola, NY, 1991), Chap. 5.
    1. Lai W. M., Rubin D., and Krempl E., Introduction to Continuum Mechanics, 4th ed. ( Butterworth-Heinemann, Burlington, MA, 2010), Chap. 5.
    1. Nightingale K., McAleavey S., and Trahey G., “ Shear-wave generation using acoustic radiation force: In vivo and ex vivo results,” Ultrasound Med. Biol. 29, 1715–1723 (2003).10.1016/j.ultrasmedbio.2003.08.008 - DOI - PubMed
    1. Bercoff J., Tanter M., and Fink M., “ Supersonic shear imaging: A new technique for soft tissue elasticity mapping,” IEEE Trans. Ultrason. Ferroelectr. Freq. Control 51, 396–409 (2004).10.1109/TUFFC.2004.1295425 - DOI - PubMed

Publication types