Adaptive Synaptogenesis Constructs Neural Codes That Benefit Discrimination
- PMID: 26176744
- PMCID: PMC4503424
- DOI: 10.1371/journal.pcbi.1004299
Adaptive Synaptogenesis Constructs Neural Codes That Benefit Discrimination
Abstract
Intelligent organisms face a variety of tasks requiring the acquisition of expertise within a specific domain, including the ability to discriminate between a large number of similar patterns. From an energy-efficiency perspective, effective discrimination requires a prudent allocation of neural resources with more frequent patterns and their variants being represented with greater precision. In this work, we demonstrate a biologically plausible means of constructing a single-layer neural network that adaptively (i.e., without supervision) meets this criterion. Specifically, the adaptive algorithm includes synaptogenesis, synaptic shedding, and bi-directional synaptic weight modification to produce a network with outputs (i.e. neural codes) that represent input patterns proportional to the frequency of related patterns. In addition to pattern frequency, the correlational structure of the input environment also affects allocation of neural resources. The combined synaptic modification mechanisms provide an explanation of neuron allocation in the case of self-taught experts.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures
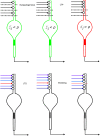

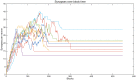
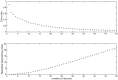
Similar articles
-
Hebbian Wiring Plasticity Generates Efficient Network Structures for Robust Inference with Synaptic Weight Plasticity.Front Neural Circuits. 2016 May 31;10:41. doi: 10.3389/fncir.2016.00041. eCollection 2016. Front Neural Circuits. 2016. PMID: 27303271 Free PMC article.
-
Representation of input structure in synaptic weights by spike-timing-dependent plasticity.Phys Rev E Stat Nonlin Soft Matter Phys. 2010 Aug;82(2 Pt 1):021912. doi: 10.1103/PhysRevE.82.021912. Epub 2010 Aug 13. Phys Rev E Stat Nonlin Soft Matter Phys. 2010. PMID: 20866842
-
Spatiotemporal learning in analog neural networks using spike-timing-dependent synaptic plasticity.Phys Rev E Stat Nonlin Soft Matter Phys. 2007 May;75(5 Pt 1):051917. doi: 10.1103/PhysRevE.75.051917. Epub 2007 May 29. Phys Rev E Stat Nonlin Soft Matter Phys. 2007. PMID: 17677108
-
Synaptic plasticity: taming the beast.Nat Neurosci. 2000 Nov;3 Suppl:1178-83. doi: 10.1038/81453. Nat Neurosci. 2000. PMID: 11127835 Review.
-
Spontaneous Network Activity and Synaptic Development.Neuroscientist. 2014 Jun;20(3):272-90. doi: 10.1177/1073858413510044. Epub 2013 Nov 25. Neuroscientist. 2014. PMID: 24280071 Free PMC article. Review.
Cited by
-
Opposing Effects of Neuronal Activity on Structural Plasticity.Front Neuroanat. 2016 Jun 28;10:75. doi: 10.3389/fnana.2016.00075. eCollection 2016. Front Neuroanat. 2016. PMID: 27445713 Free PMC article. Review.
-
The information theory of developmental pruning: Optimizing global network architectures using local synaptic rules.PLoS Comput Biol. 2021 Oct 11;17(10):e1009458. doi: 10.1371/journal.pcbi.1009458. eCollection 2021 Oct. PLoS Comput Biol. 2021. PMID: 34634045 Free PMC article.
-
Limited synapse overproduction can speed development but sometimes with long-term energy and discrimination penalties.PLoS Comput Biol. 2017 Sep 22;13(9):e1005750. doi: 10.1371/journal.pcbi.1005750. eCollection 2017 Sep. PLoS Comput Biol. 2017. PMID: 28937989 Free PMC article.
-
Distinctive properties of biological neural networks and recent advances in bottom-up approaches toward a better biologically plausible neural network.Front Comput Neurosci. 2023 Jun 28;17:1092185. doi: 10.3389/fncom.2023.1092185. eCollection 2023. Front Comput Neurosci. 2023. PMID: 37449083 Free PMC article. Review.
References
-
- Levy WB, Desmond NL. The rules of elemental synaptic plasticity In: Levy WB, Anderson JA, Lehmkule S, editors. Synaptic modification, neuron selectivity, and nervous system organization. Hillsdale, NJ: Erlbaum; 1985. p. 105–121.
-
- Levy WB, Colbert CM, Desmond NL. Elemental adaptive processes of neurons and synapses: a statistical/computational perspective In: Gluck MA, Rumelhart DE, editors. Neuroscience and Connectionist Theory. Hillsdale, NJ: Erlbaum; 1990. p. 187–235.
-
- Dammasch IE, Wagner GP, Wolff JR. Self-stabilization of neuronal networks. Biological cybernetics. 1986; 54(4–5): 211–22. - PubMed
-
- Miller K. Equivalence of a sprouting-and-retraction model and correlation-based plasticity models of neural development. Neural Computation. 1998; 10(3): 529–47. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

