Model averaging, optimal inference, and habit formation - PubMed Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2014 Jun 26:8:457.
doi: 10.3389/fnhum.2014.00457. eCollection 2014.

Model averaging, optimal inference, and habit formation

Thomas H B FitzGerald  1 , Raymond J Dolan  1 , Karl J Friston  1
Affiliations

Model averaging, optimal inference, and habit formation

Thomas H B FitzGerald et al. Front Hum Neurosci. .

Abstract

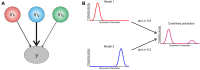
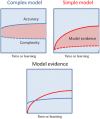
Postulating that the brain performs approximate Bayesian inference generates principled and empirically testable models of neuronal function-the subject of much current interest in neuroscience and related disciplines. Current formulations address inference and learning under some assumed and particular model. In reality, organisms are often faced with an additional challenge-that of determining which model or models of their environment are the best for guiding behavior. Bayesian model averaging-which says that an agent should weight the predictions of different models according to their evidence-provides a principled way to solve this problem. Importantly, because model evidence is determined by both the accuracy and complexity of the model, optimal inference requires that these be traded off against one another. This means an agent's behavior should show an equivalent balance. We hypothesize that Bayesian model averaging plays an important role in cognition, given that it is both optimal and realizable within a plausible neuronal architecture. We outline model averaging and how it might be implemented, and then explore a number of implications for brain and behavior. In particular, we propose that model averaging can explain a number of apparently suboptimal phenomena within the framework of approximate (bounded) Bayesian inference, focusing particularly upon the relationship between goal-directed and habitual behavior.

Keywords: Bayesian inference; active inference; habit; interference effect; predictive coding.

PubMed Disclaimer

Figures

Figure 1
Figure 1
Cartoon illustrating inference (A), learning (B), and model comparison (C). Inference requires an agent to alter its beliefs about the causes (u1, u2) of sensory data (y) to maximize model evidence (minimize surprise). Learning also involves the maximization of model evidence, this time through adjustment of the parameters of the model (the mapping between hidden causes and observations). Model comparison involves averaging over—or selecting from—alternative models that can be used for inference and learning.
Figure 2
Figure 2
(A) Graphical illustration of Bayesian model averaging. To generate a single Bayes optimal prediction about data y, the predictions of three models m1−3 are weighted according to their posterior probabilities [see Equation (A5)]. Here model two has the largest posterior probability, and thus its prediction is weighted most strongly. (B) Cartoon explaining interference effects using model comparison. An agent entertains two models of the world, which make different predictions about the probability of making an action based on some movement parameter (x axis). The model probabilities for these are p(m1) = 0.8 and p(m2) = 0.2 respectively, and the resulting weighted prediction (magenta) shows an interference effect based on this weighted averaging [see Equation (A5)].
Figure 3
Figure 3
This schematic illustrates the possibility that a more complex model may have greater model evidence at the start of learning but will then give way to a simpler model as their parameters are optimized. The upper panels show the learning-related improvement in accuracy and complexity for a complex model (left panel) and a simple model (right panel). The model evidence is shown as the difference (pink areas). The more complex model explains the data more accurately but with a greater complexity cost, that is finessed during the learning. Conversely, the simpler model will always have a lower accuracy but can (with learning) attain greater model evidence—and thereby be selected by Bayesian model averaging as time proceeds and the active inference becomes habitual.
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Acuña D. E., Schrater P. (2010). Structure learning in human sequential decision-making. PLoS Comput. Biol. 6:e1001003 10.1371/journal.pcbi.1001003 - DOI - PMC - PubMed
    1. Adams C., Dickinson A. (1981). Instrumental responding following reinforcer devaluation. Q. J. Exp. Psychol. 33, 109–121 10.1080/14640748108400816 - DOI
    1. Adams R. A., Stephan K. E., Brown H. R., Frith C. D., Friston K. J. (2013). The computational anatomy of psychosis. Front. Psychiatry 4:47 10.3389/fpsyt.2013.00047 - DOI - PMC - PubMed
    1. Attias H. (2000). A variational Bayesian framework for graphical models. Adv. Neural Inf. Process. Syst. 12, 209–215
    1. Bach D. R., Dolan R. J. (2012). Knowing how much you don't know: a neural organization of uncertainty estimates. Nat. Rev. Neurosci. 13, 572–586 10.1038/nrn3289 - DOI - PubMed

LinkOut - more resources