Optimal design for hetero-associative memory: hippocampal CA1 phase response curve and spike-timing-dependent plasticity
- PMID: 24204822
- PMCID: PMC3812027
- DOI: 10.1371/journal.pone.0077395
Optimal design for hetero-associative memory: hippocampal CA1 phase response curve and spike-timing-dependent plasticity
Abstract
Recently reported experimental findings suggest that the hippocampal CA1 network stores spatio-temporal spike patterns and retrieves temporally reversed and spread-out patterns. In this paper, we explore the idea that the properties of the neural interactions and the synaptic plasticity rule in the CA1 network enable it to function as a hetero-associative memory recalling such reversed and spread-out spike patterns. In line with Lengyel's speculation (Lengyel et al., 2005), we firstly derive optimally designed spike-timing-dependent plasticity (STDP) rules that are matched to neural interactions formalized in terms of phase response curves (PRCs) for performing the hetero-associative memory function. By maximizing object functions formulated in terms of mutual information for evaluating memory retrieval performance, we search for STDP window functions that are optimal for retrieval of normal and doubly spread-out patterns under the constraint that the PRCs are those of CA1 pyramidal neurons. The system, which can retrieve normal and doubly spread-out patterns, can also retrieve reversed patterns with the same quality. Finally, we demonstrate that purposely designed STDP window functions qualitatively conform to typical ones found in CA1 pyramidal neurons.
Conflict of interest statement
Figures

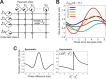
 are characterized by their initial phases,
are characterized by their initial phases,  , representing their individual spiking timings. The angle of the radius line in the circle represents the initial phase. Postsynaptic neurons numbered
, representing their individual spiking timings. The angle of the radius line in the circle represents the initial phase. Postsynaptic neurons numbered  are characterized by their initial phases,
are characterized by their initial phases,  . The pre- and postsynaptic neurons are fully connected by
. The pre- and postsynaptic neurons are fully connected by  synaptic connections. (B) Phase response curves (PRCs) of hippocampal CA1 pyramidal neurons recorded in vitro
, . The abscissa represents the phase of a perturbation arrival, and the ordinate represents the phase shift of the postsynaptic spike in response to the perturbation current. (C) Typical STDP window functions observed in hippocampal CA1 pyramidal neurons. In the storage process, synaptic weights
synaptic connections. (B) Phase response curves (PRCs) of hippocampal CA1 pyramidal neurons recorded in vitro
, . The abscissa represents the phase of a perturbation arrival, and the ordinate represents the phase shift of the postsynaptic spike in response to the perturbation current. (C) Typical STDP window functions observed in hippocampal CA1 pyramidal neurons. In the storage process, synaptic weights  are determined in accordance with an STDP learning rule depending on the phase difference between the pre- and postsynaptic spikes. Left: Symmetric plasticity rule . Right: Asymmetric plasticity rule .
are determined in accordance with an STDP learning rule depending on the phase difference between the pre- and postsynaptic spikes. Left: Symmetric plasticity rule . Right: Asymmetric plasticity rule .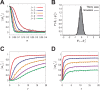
 1 in Fig. 2B
[18]) measured from hippocampal CA1 pyramidal neurons. In this simulation,
1 in Fig. 2B
[18]) measured from hippocampal CA1 pyramidal neurons. In this simulation,  . Given a retrieval key pattern similar to
. Given a retrieval key pattern similar to  ,
,  is to be retrieved (i.e., normal spike pattern retrieval). (A) Amplitudes of the overlaps
is to be retrieved (i.e., normal spike pattern retrieval). (A) Amplitudes of the overlaps  (
( denotes the wavenumber) at equilibrium as a function of the noise intensity
denotes the wavenumber) at equilibrium as a function of the noise intensity  when
when  . As defined in Eq. (26),
. As defined in Eq. (26),  is the overlap between the first memory output pattern
is the overlap between the first memory output pattern  and the retrieval output pattern
and the retrieval output pattern  in the
in the  -th frequency component:
-th frequency component:  .
.  represents the characteristic function of the postsynaptic phase distribution
represents the characteristic function of the postsynaptic phase distribution  at each wavenumber
at each wavenumber  . Solid curves are theoretical results obtained from Eq. (27); The plotted points are from numerical simulations using LPE (13). (B) An example of the PDF (19) and a histogram of phase difference
. Solid curves are theoretical results obtained from Eq. (27); The plotted points are from numerical simulations using LPE (13). (B) An example of the PDF (19) and a histogram of phase difference  obtained by numerically solving the LPE (13) at equilibrium.
obtained by numerically solving the LPE (13) at equilibrium.  and
and  . (C) Amplitudes of the overlaps
. (C) Amplitudes of the overlaps  (
( ) as a function of the concentration parameter
) as a function of the concentration parameter  . As defined in Eq. (12),
. As defined in Eq. (12),  is the overlap between the first memory key pattern
is the overlap between the first memory key pattern  and the retrieval key pattern
and the retrieval key pattern  in the
in the  -th frequency component:
-th frequency component:  .
.  represents the characteristic function of the presynaptic phase distribution
represents the characteristic function of the presynaptic phase distribution  at each wavenumber
at each wavenumber  . Solid curves are theoretical results obtained from Eq. (15); Plots are obtained from a retrieval key pattern randomly generated with the von Mises PDF (14). (D) Amplitudes of the overlaps
. Solid curves are theoretical results obtained from Eq. (15); Plots are obtained from a retrieval key pattern randomly generated with the von Mises PDF (14). (D) Amplitudes of the overlaps  (
( ) at equilibrium as a function of
) at equilibrium as a function of  .
.  . Solid curves are theoretical results obtained from Eq. (27); The plots are from numerical simulations using LPE (13).
. Solid curves are theoretical results obtained from Eq. (27); The plots are from numerical simulations using LPE (13).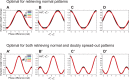
 defined in Eq. (25), we searched for STDP window functions that are optimal for retrieving normal patterns. (A′–D′) By maximizing the objective function
defined in Eq. (25), we searched for STDP window functions that are optimal for retrieving normal patterns. (A′–D′) By maximizing the objective function  defined in Eq. (24), we searched for ones that are optimal for both retrieving normal and doubly spread-out patterns. In all cases,
defined in Eq. (24), we searched for ones that are optimal for both retrieving normal and doubly spread-out patterns. In all cases,  ,
,  . We obtained connected sets of optimal STDP window functions, as described in the main article. Each of the four panels in the upper and lower rows plots examples of optimal STDP window functions with different phases. The numbers assigned to each line correspond to the cell indexes in Fig. 2B. All sets of optimal STDP window functions except for cell #1 have the same form. (A, A′) STDP window functions when
. We obtained connected sets of optimal STDP window functions, as described in the main article. Each of the four panels in the upper and lower rows plots examples of optimal STDP window functions with different phases. The numbers assigned to each line correspond to the cell indexes in Fig. 2B. All sets of optimal STDP window functions except for cell #1 have the same form. (A, A′) STDP window functions when  , which corresponds to the symmetric STDP rule. (B, B′) STDP window functions when
, which corresponds to the symmetric STDP rule. (B, B′) STDP window functions when  (B) and
(B) and  (B′), which correspond to the asymmetric STDP rule. (C, C′) STDP window functions when
(B′), which correspond to the asymmetric STDP rule. (C, C′) STDP window functions when  , which corresponds to the inverted symmetric STDP rule. (D, D′) STDP window functions when
, which corresponds to the inverted symmetric STDP rule. (D, D′) STDP window functions when  (D) and
(D) and  (D′), which correspond to the inverted asymmetric STDP rule.
(D′), which correspond to the inverted asymmetric STDP rule.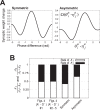
 and
and  . Symmetric: left panel of Fig. 5A
. Asymmetric: right panel of Fig. 5A
.
. Symmetric: left panel of Fig. 5A
. Asymmetric: right panel of Fig. 5A
.
 was determined using the STDP window function (cell
was determined using the STDP window function (cell  5 in Fig. 4A′) to store three pairs of random phase patterns,
5 in Fig. 4A′) to store three pairs of random phase patterns,  and
and  (
( ), and when presented with the retrieval key pattern generated with the conditional PDF (Eq. (14)) given
), and when presented with the retrieval key pattern generated with the conditional PDF (Eq. (14)) given  , the retrieval performance of the system with the determined synaptic weight and the measured PRC (cell #5 in Fig. 2B) was verified by using numerical simulations (
, the retrieval performance of the system with the determined synaptic weight and the measured PRC (cell #5 in Fig. 2B) was verified by using numerical simulations ( ,
,  ,
,  ). (A) Normal spike pattern retrieval (
). (A) Normal spike pattern retrieval ( ). (B) Reversed pattern retrieval (
). (B) Reversed pattern retrieval ( ). (C) Doubly spread-out pattern retrieval (
). (C) Doubly spread-out pattern retrieval ( ). Left column: Time evolution of the amplitude of the overlap between the
). Left column: Time evolution of the amplitude of the overlap between the  -th frequency component of
-th frequency component of  and the
and the  -th frequency component of
-th frequency component of  ,
,  . Center column: An example of the memory output pattern as originally stored,
. Center column: An example of the memory output pattern as originally stored,  . Right column: The retrieval output pattern
. Right column: The retrieval output pattern  at equilibrium (corresponding to
at equilibrium (corresponding to  in left column).
in left column).Similar articles
-
GABAA receptor-mediated feedforward and feedback inhibition differentially modulate hippocampal spike timing-dependent plasticity.Biochem Biophys Res Commun. 2012 Oct 26;427(3):466-72. doi: 10.1016/j.bbrc.2012.08.081. Epub 2012 Aug 24. Biochem Biophys Res Commun. 2012. PMID: 22940549
-
Matching storage and recall: hippocampal spike timing-dependent plasticity and phase response curves.Nat Neurosci. 2005 Dec;8(12):1677-83. doi: 10.1038/nn1561. Epub 2005 Oct 30. Nat Neurosci. 2005. PMID: 16261136
-
A computational study on plasticity during theta cycles at Schaffer collateral synapses on CA1 pyramidal cells in the hippocampus.Hippocampus. 2015 Feb;25(2):208-18. doi: 10.1002/hipo.22365. Epub 2014 Sep 25. Hippocampus. 2015. PMID: 25220633
-
Voltage Imaging in the Study of Hippocampal Circuit Function and Plasticity.Adv Exp Med Biol. 2015;859:197-211. doi: 10.1007/978-3-319-17641-3_8. Adv Exp Med Biol. 2015. PMID: 26238054 Review.
-
Does spike timing-dependent synaptic plasticity underlie memory formation?Clin Exp Pharmacol Physiol. 2007 Oct;34(10):1070-6. doi: 10.1111/j.1440-1681.2007.04724.x. Clin Exp Pharmacol Physiol. 2007. PMID: 17714096 Review.
Cited by
-
Distinctive properties of biological neural networks and recent advances in bottom-up approaches toward a better biologically plausible neural network.Front Comput Neurosci. 2023 Jun 28;17:1092185. doi: 10.3389/fncom.2023.1092185. eCollection 2023. Front Comput Neurosci. 2023. PMID: 37449083 Free PMC article. Review.
-
Heteroassociative storage of hippocampal pattern sequences in the CA3 subregion.PeerJ. 2018 Jan 2;6:e4203. doi: 10.7717/peerj.4203. eCollection 2018. PeerJ. 2018. PMID: 29312826 Free PMC article.
-
Integration of exteroceptive and interoceptive information within the hippocampus: a computational study.Front Syst Neurosci. 2015 Jun 5;9:87. doi: 10.3389/fnsys.2015.00087. eCollection 2015. Front Syst Neurosci. 2015. PMID: 26097448 Free PMC article.
References
-
- Skaggs WE, McNaughton BL (1996) Replay of neuronal firing sequences in rat hippocampus during sleep following spatial experience. Science 271: 1870–1873. - PubMed
-
- Lee AK, Wilson MA (2002) Memory of sequential experience in the hippocampus during slow wave sleep. Neuron 36: 1183–1194. - PubMed
-
- Ji D, Wilson MA (2007) Coordinated memory replay in the visual cortex and hippocampus during sleep. Nat Neurosci 10: 100–107. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Medical
Miscellaneous

