The anatomy of choice: active inference and agency - PubMed Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2013 Sep 25:7:598.
doi: 10.3389/fnhum.2013.00598. eCollection 2013.

The anatomy of choice: active inference and agency

Karl Friston  1 , Philipp Schwartenbeck, Thomas Fitzgerald, Michael Moutoussis, Timothy Behrens, Raymond J Dolan
Affiliations

The anatomy of choice: active inference and agency

Karl Friston et al. Front Hum Neurosci. .

Abstract

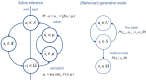
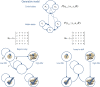
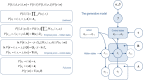
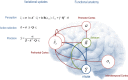
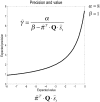
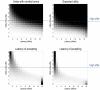
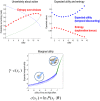
This paper considers agency in the setting of embodied or active inference. In brief, we associate a sense of agency with prior beliefs about action and ask what sorts of beliefs underlie optimal behavior. In particular, we consider prior beliefs that action minimizes the Kullback-Leibler (KL) divergence between desired states and attainable states in the future. This allows one to formulate bounded rationality as approximate Bayesian inference that optimizes a free energy bound on model evidence. We show that constructs like expected utility, exploration bonuses, softmax choice rules and optimism bias emerge as natural consequences of this formulation. Previous accounts of active inference have focused on predictive coding and Bayesian filtering schemes for minimizing free energy. Here, we consider variational Bayes as an alternative scheme that provides formal constraints on the computational anatomy of inference and action-constraints that are remarkably consistent with neuroanatomy. Furthermore, this scheme contextualizes optimal decision theory and economic (utilitarian) formulations as pure inference problems. For example, expected utility theory emerges as a special case of free energy minimization, where the sensitivity or inverse temperature (of softmax functions and quantal response equilibria) has a unique and Bayes-optimal solution-that minimizes free energy. This sensitivity corresponds to the precision of beliefs about behavior, such that attainable goals are afforded a higher precision or confidence. In turn, this means that optimal behavior entails a representation of confidence about outcomes that are under an agent's control.

Keywords: Bayesian; active inference; agency; bounded rationality; embodied cognition; free energy; inference; utility theory.

PubMed Disclaimer

Figures

Figure 1
Figure 1
Left panel: this is a schematic of the dependencies among variables underlying active inference. Here, a generative process representing state transitions in the real world generates observations or outcomes that are used to update the internal states of an agent. These internal states encode the sufficient statistics of an approximate posterior distribution over variables defined by a generative model (right panel). Particular sufficient statistics, encoding beliefs about choices or control states are reflexively transcribed into action, which affects real state transitions—thereby closing the action–perception cycle. Right panel: notice that the generative model, which defines free energy has a much simpler form. It simply supposes that there are mutually dependent hidden and control states that conspire to produce observations.
Figure 2
Figure 2
Upper panel: this is an example of a generative model, based on a hierarchical hidden Markov model. The key feature of this model is that there are two sets of states; hidden states and control states. The transitions among one set of states depend upon the state occupied in the other set. Lower panels: this provides an example of a particular generative model in which there are two control states; reject (stay) or accept (shift). The control state determines the transitions amongst the hidden states which, in this example, comprise a low offer (first state), a high offer (second state), a no-offer state (third state), and absorbing states that are entered whenever a low (fourth state) or high (fifth state) offer is accepted. The probability of moving from one state to another is one, unless specified by the values of the (control dependent) transition probabilities shown in the middle row. For example, the parameter r controls the rate of offer withdrawal (cf. a hazard rate). Note that absorbing states—that re-enter themselves with unit probability—render this Markovian process irreversible. We will use this example in simulations of choice behavior.
Figure 3
Figure 3
This figure illustrates the temporal dependencies among hidden states and control states in the generative model considered in this paper. This Bayesian graph illustrates the dependencies among successive hidden states and how they depend upon action in the past and control states in the future. Note that future control states depend upon the current state because it depends upon the relative entropy or divergence between distributions over the final state that are, and are not, conditioned on the current state. The resulting choices depend upon the precision of beliefs about control states, which, in turn depend upon the parameters of the model. Observed outcomes depend on, and only on, the hidden states at any given time.
Figure 4
Figure 4
This figure illustrates the cognitive and functional anatomy implied by the variational scheme—or more precisely, the mean field assumption implicit in variational updates. Here, we have associated the variational updates of expected states with perception, of future control states (policies) within action selection and, finally, expected precision with evaluation. The forms of these updates suggest the sufficient statistics from each subset are passed among each other until convergence to an internally consistent (Bayes optimal) solution. In terms of neuronal implementation, this might be likened to the exchange of neuronal signals via extrinsic connections among functionally specialized brain systems. In this (purely iconic) schematic, we have associated perception (inference about the current state of the world) with the prefrontal cortex, while assigning action selection to the basal ganglia. Crucially, precision has been associated with dopaminergic projections from the ventral tegmental area and substantia nigra that, necessarily, project to both cortical (perceptual) and subcortical (action selection) systems. See main text for a full description of the equations.
Figure 5
Figure 5
The strictly increasing, monotonic relationship between expected precision and expected value. Note that value never exceeds zero. This is because a Kullback–Leibler divergence can never be less than zero; by Gibbs inequality.
Figure 6
Figure 6
This figure shows the results of a simulation of 16 trials, where a low offer was replaced by high offer on the 11th trial, which was accepted on the subsequent trial. The upper left panel shows the expected states as a function of trials or time, where the states are defined in Figure 2. The upper right panel shows the corresponding expectations about control in the future, where the dotted lines are expectations during earlier trials and the full lines correspond to expectations during the final trial. Blue corresponds to reject (stay) and green to accept (shift). The lower panels show the time-dependent changes in expected precision, after convergence on each trial (lower left) and deconvolved updates after each iteration of the variational updates (lower right).
Figure 7
Figure 7
This figure uses the same format as the previous figure; however, here, the low offer was withdrawn on the fifth trial, leading to a decrease in expected precision. Note the difference (divergence) between the expected states on the 15th (penultimate) and 16 (final) trial. It is this large divergence (or more exactly the divergence between distributions over the final state) that leads to a small value and associated precision.
Figure 8
Figure 8
The upper panels show the probability of accepting with (left) and without (right) the entropy or novelty part of value, where the low offer remained available and action was precluded. These probabilities are shown as a function of trial number and the relative utility of the low offer (white corresponds to high probabilities). The lower panels show the same results but in terms of the probability distribution over the latency or time to choice. Note that including the entropy in value slightly delays the time to choice—to ensure a greater latitude of options. This is particularly noticeable in the ambiguous situation when the low offer has the same utility as the high offer (of four).
Figure 9
Figure 9
Upper left panel: the probability of accepting an offer as a function of time or trials. Note that the probability of accepting (green) increases over time to approach and surpass the probability of rejection. This produces an increase in the uncertainty about action—shown in red. Upper right panel: these are the expected utility and entropy components of expected value as a function of trial number. The key result here is the time-dependent change in expected utility, which corresponds to temporal discounting of the expected utility: i.e., the expected utility of the final state is greater when there are fewer intervening trials. Lower panel: the marginal utility of the high offer (green) and low offer (blue) as a function of the relative utility of the high offer. Marginal utility is defined here as expected utility times expected precision. The multiple curves correspond to the marginal utilities as a function of trial number (and do not differ greatly because expected precision changes more slowly over time—for a given utility—than it changes over utility—for a given time).
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Ashby W. R. (1947). Principles of the self-organizing dynamic system. J. Gen. Psychol. 37, 125–128 10.1080/00221309.1947.9918144 - DOI - PubMed
    1. Bastos A. M., Usrey W. M., Adams R. A., Mangun G. R., Fries P., Friston K. J. (2012). Canonical microcircuits for predictive coding. Neuron 76, 695–711 10.1016/j.neuron.2012.10.038 - DOI - PMC - PubMed
    1. Beal M. J. (2003). Variational Algorithms for Approximate Bayesian Inference. Ph.D. thesis, University College London.
    1. Birkhoff G. D. (1931). Proof of the ergodic theorem. Proc. Natl. Acad. Sci. U.S.A. 17, 656–660 10.1073/pnas.17.12.656 - DOI - PMC - PubMed
    1. Braun D. A., Ortega P. A., Theodorou E., Schaal S. (2011). Path integral control and bounded rationality, in IEEE Symposium on Adaptive Dynamic Programming and Reinforcement Learning (ADPRL) (Paris: IEEE; ), 202–209

LinkOut - more resources