Post hoc Bayesian model selection
- PMID: 21459150
- PMCID: PMC3112494
- DOI: 10.1016/j.neuroimage.2011.03.062
Post hoc Bayesian model selection
Abstract
This note describes a Bayesian model selection or optimization procedure for post hoc inferences about reduced versions of a full model. The scheme provides the evidence (marginal likelihood) for any reduced model as a function of the posterior density over the parameters of the full model. It rests upon specifying models through priors on their parameters, under the assumption that the likelihood remains the same for all models considered. This provides a quick and efficient scheme for scoring arbitrarily large numbers of models, after inverting a single (full) model. In turn, this enables the selection among discrete models that are distinguished by the presence or absence of free parameters, where free parameters are effectively removed from the model using very precise shrinkage priors. An alternative application of this post hoc model selection considers continuous model spaces, defined in terms of hyperparameters (sufficient statistics) of the prior density over model parameters. In this instance, the prior (model) can be optimized with respect to its evidence. The expressions for model evidence become remarkably simple under the Laplace (Gaussian) approximation to the posterior density. Special cases of this scheme include Savage-Dickey density ratio tests for reduced models and automatic relevance determination in model optimization. We illustrate the approach using general linear models and a more complicated nonlinear state-space model.
Copyright © 2011 Elsevier Inc. All rights reserved.
Figures
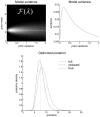
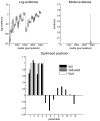
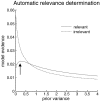
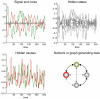

Similar articles
-
A caveat on the Savage-Dickey density ratio: The case of computing Bayes factors for regression parameters.Br J Math Stat Psychol. 2019 May;72(2):316-333. doi: 10.1111/bmsp.12150. Epub 2018 Nov 19. Br J Math Stat Psychol. 2019. PMID: 30451277
-
Variational free energy and the Laplace approximation.Neuroimage. 2007 Jan 1;34(1):220-34. doi: 10.1016/j.neuroimage.2006.08.035. Epub 2006 Oct 20. Neuroimage. 2007. PMID: 17055746
-
Objective Bayesian search of Gaussian directed acyclic graphical models for ordered variables with non-local priors.Biometrics. 2013 Jun;69(2):478-87. doi: 10.1111/biom.12018. Epub 2013 Apr 5. Biometrics. 2013. PMID: 23560520
-
Nonconjugate Bayesian analysis of variance component models.Biometrics. 2000 Sep;56(3):768-74. doi: 10.1111/j.0006-341x.2000.00768.x. Biometrics. 2000. PMID: 10985214
-
Avoiding pitfalls: Bayes factors can be a reliable tool for post hoc data selection in implicit learning.Psychon Bull Rev. 2021 Dec;28(6):1848-1859. doi: 10.3758/s13423-021-01901-4. Epub 2021 Mar 25. Psychon Bull Rev. 2021. PMID: 33768502 Review.
Cited by
-
Computational Modeling of Oddball Sequence Processing Exposes Common and Differential Auditory Network Changes in First-Episode Schizophrenia-Spectrum Disorders and Schizophrenia.Schizophr Bull. 2023 Mar 15;49(2):407-416. doi: 10.1093/schbul/sbac153. Schizophr Bull. 2023. PMID: 36318221 Free PMC article.
-
Effective connectivity predicts cognitive empathy in cocaine addiction: a spectral dynamic causal modeling study.Brain Imaging Behav. 2021 Jun;15(3):1553-1561. doi: 10.1007/s11682-020-00354-y. Brain Imaging Behav. 2021. PMID: 32710329
-
An electrophysiological validation of stochastic DCM for fMRI.Front Comput Neurosci. 2013 Jan 18;6:103. doi: 10.3389/fncom.2012.00103. eCollection 2012. Front Comput Neurosci. 2013. PMID: 23346055 Free PMC article.
-
Federated inference and belief sharing.Neurosci Biobehav Rev. 2024 Jan;156:105500. doi: 10.1016/j.neubiorev.2023.105500. Epub 2023 Dec 5. Neurosci Biobehav Rev. 2024. PMID: 38056542 Free PMC article. Review.
-
Altered Effective Connectivity Measured by Resting-State Functional Magnetic Resonance Imaging in Posterior Parietal-Frontal-Striatum Circuit in Patients With Disorder of Consciousness.Front Neurosci. 2022 Jan 20;15:766633. doi: 10.3389/fnins.2021.766633. eCollection 2021. Front Neurosci. 2022. PMID: 35153656 Free PMC article.
References
-
- Beal M.J., Ghahramani Z. The variational Bayesian EM algorithm for incomplete Data: with application to scoring graphical model structures. In: Bernardo J.M., Bayarri M.J., Berger J.O., Dawid A.P., Heckerman D., Smith A.F.M., West M., editors. Bayesian Statistics. OUP; UK: 2003. Chapter 7.
-
- Beal M.J. (1998) Variational algorithms for approximate Bayesian inference, PhD Thesis:http://www.cse.buffalo.edu/faculty/mbeal/thesis/- p58.
-
- Dempster A.P., Laird N.M., Rubin Maximum likelihood from incomplete data via the EM algorithm. J. Roy. Stat. Soc. B. 1977;39:1–38.
-
- Dickey J. The weighted likelihood ratio, linear hypotheses on normal location parameters. Ann. Stat. 1971;42:204–223.
-
- Efron B., Morris C. Stein's estimation rule and its competitors—an empirical Bayes approach. J. Am. Stats. Assoc. 1973;68:117–130.
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources

