Network clustering: probing biological heterogeneity by sparse graphical models - PubMed Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2011 Apr 1;27(7):994-1000.
doi: 10.1093/bioinformatics/btr070. Epub 2011 Feb 10.

Network clustering: probing biological heterogeneity by sparse graphical models

Sach Mukherjee  1 , Steven M Hill
Affiliations

Network clustering: probing biological heterogeneity by sparse graphical models

Sach Mukherjee et al. Bioinformatics. .

Abstract

Motivation: Networks and pathways are important in describing the collective biological function of molecular players such as genes or proteins. In many areas of biology, for example in cancer studies, available data may harbour undiscovered subtypes which differ in terms of network phenotype. That is, samples may be heterogeneous with respect to underlying molecular networks. This motivates a need for unsupervised methods capable of discovering such subtypes and elucidating the corresponding network structures.

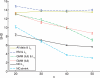
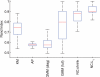
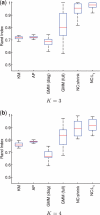
Results: We exploit recent results in sparse graphical model learning to put forward a 'network clustering' approach in which data are partitioned into subsets that show evidence of underlying, subset-level network structure. This allows us to simultaneously learn subset-specific networks and corresponding subset membership under challenging small-sample conditions. We illustrate this approach on synthetic and proteomic data.

Availability: go.warwick.ac.uk/sachmukherjee/networkclustering.

PubMed Disclaimer

Figures

Fig. 1.
Fig. 1.
Simulated data, clustering results. Boxplots over the Rand index with respect to true cluster membership (higher scores indicate better agreement with the true clustering; a score of unity indicates perfect agreement) are shown for sample sizes of (a) n = 20, (b) n = 30, (c) n = 40 and (d) n = 50 per cluster. Data were generated for two clusters from known sparse network models (for details see text), with 100 iterations carried out at each sample size. Results shown for K-means (KM), affinity propagation (AP), diagonal-covariance Gaussian mixture model [GMM (diag)], full-covariance GMM [GMM (full)], network clustering using shrinkage-based network learning (NC:shrink) and ℓ1-penalized network clustering (NC:L1). (For n = 20 the full-covariance GMM could not be used as small-sample effects meant that it did not yield valid covariance matrices.)
Fig. 2.
Fig. 2.
Simulated data, network reconstruction. Distance between true and inferred networks, in terms of the number of edge differences or ‘Structural Hamming Distance (SHD; smaller values indicate closer approximation to true network) for simulated data at sample sizes of n = 20, 30, 40, 50 per cluster. Results shown for: ℓ1-penalized network inference applied to complete data, without clustering (‘All Data & L1’); K-means clustering followed by ℓ1-penalized network inference applied to the clusters discovered (‘KM & L1’); clustering using a (full covariance) Gaussian mixture model followed by ℓ1-penalized network inference [‘GMM (full) & L1’]; full covariance GMM [‘GMM (full)’]; network clustering using ℓ1-penalized network inference (‘NC:L1’); and network clustering using shrinkage-based network inference (‘NC:shrink’). Mean SHD over 100 iterations are shown, and error bars indicate SEM.
Fig. 3.
Fig. 3.
Phospho-proteomic and synthetic data, clustering results. Boxplots over the Rand index with respect to true cluster membership (score of unity indicates perfect agreement with the true clustering). Data with a known, gold-standard cluster assignment were created using phospho-proteomic data from Sachs et al. (2005) as described in text. Boxplots are over 100 subsampling iterations; per-cluster sample size was n = 40; algorithms used were K-means (KM), affinity propagation (AP), diagonal-covariance Gaussian mixture model [GMM (diag)], full-covariance GMM [GMM (full)], network clustering using shrinkage-based network inference (NC:shrink) and ℓ1-penalized network clustering (NC:L1).
Fig. 4.
Fig. 4.
Phospho-proteomic and synthetic data, network reconstruction. (a) SHD between correct and inferred networks. Results shown for ℓ1-penalized network inference applied to complete data, without clustering (‘All Data & L1’); K-means clustering followed by ℓ1-penalized network inference applied to the clusters discovered (‘KM & L1’); clustering using a (full covariance) Gaussian mixture model followed by ℓ1-penalized network inference [GMM (full) & L1’]; clustering and network inference using a GMM [‘GMM (full)’]; network clustering using ℓ1-penalized network inference (‘NC:L1’); and network clustering using shrinkage-based network inference (‘NC:shrink’). Mean SHD over 100 subsampling iterations were shown, and error bars indicate SDs; (b) Correct sparsity pattern. Correct, large-sample sparsity pattern for proteomic data of Sachs et al. (2005); (c) NC:l1. Inverse covariance recovered from small-sample, heterogenous data by ℓ1-penalized network clustering and (d) All data (no clustering)-l1. Inverse covariance from ℓ1-penalized network inference applied directly to the complete, heterogenous data (see text for full details; per-cluster sample size n = 40; red and blue indicate negative and positive values, respectively).
Fig. 5.
Fig. 5.
Simulated data, clustering results for K = 3, 4 clusters. Boxplots over the Rand index with respect to true cluster membership are shown for data consisting of (a) K = 3 clusters and (b) K = 4 clusters, with per cluster sample size of n = 50. Data were generated from known sparse network models (for details see text), with 25 iterations carried out at each sample size. Results shown for K-means (KM), affinity propagation (AP), diagonal-covariance Gaussian mixture model [GMM (diag)], full-covariance GMM [GMM (full)], network clustering using shrinkage-based network inference (NC:shrink) and ℓ1-penalized network clustering (NC:L1).
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Banerjee O., et al. Model selection through sparse maximum likelihood estimation for multivariate Gaussian or binary data. J. Mach. Learn. Res. 2008;9:485–516.
    1. Chuang H.Y., et al. Network-based classification of breast cancer metastasis. Mol. Syst. Biol. 2007;3 Article 140. - PMC - PubMed
    1. Dempster A.P. Covariance selection. Biometrics. 1972;28:157–175.
    1. Dobra A., et al. Sparse graphical models for exploring gene expression data. J. Multivar. Anal. 2004;90:196–212.
    1. Frey B.J., Dueck D. Clustering by passing messages between data points. Science. 2007;315:972–976. - PubMed

Publication types