Evaluation of the angular spectrum approach for simulations of near-field pressures - PubMed Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2008 Jan;123(1):68-76.
doi: 10.1121/1.2812579.

Evaluation of the angular spectrum approach for simulations of near-field pressures

Xiaozheng Zeng  1 , Robert J McGough
Affiliations

Evaluation of the angular spectrum approach for simulations of near-field pressures

Xiaozheng Zeng et al. J Acoust Soc Am. 2008 Jan.

Abstract

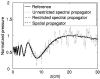
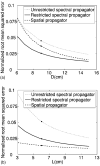
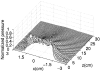
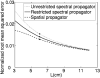
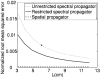
The implementation of the angular spectrum approach based on the two-dimensional fast Fourier transform is evaluated for near-field pressure simulations of square ultrasound transducers, where the three-dimensional pressure field is calculated from the normal velocity distribution on the transducer surface. The pressure field is propagated in the spatial frequency domain with the spatial propagator or the spectral propagator. The spatial propagator yields accurate results in the central portion of the computational grid while significant errors are produced near the edge due to the finite extent of the window applied to the spatial propagator. Likewise, the spectral propagator is inherently undersampled in the spatial frequency domain, and this causes high frequency errors in the computed pressure field. This aliasing problem is alleviated with angular restriction. The results show that, in nonattenuating media, the spatial propagator achieves smaller errors than the spectral propagator after the region of interest is truncated to exclude the windowing error. For pressure calculations in attenuating media or with apodized pistons as sources, the spatial and spectral propagator achieve similar accuracies. In all simulations, the angular spectrum calculations with the spatial propagator take more time than calculations with the spectral propagator.

PubMed Disclaimer

Figures

FIG. 1
FIG. 1
(Color online) The D×D source plane consisting of a nonzero normal particle velocity distribution in a 2a×2a square area on the piston surface. The remaining area is filled with zeros.
FIG. 2
FIG. 2
A two-dimensional cross section of the three-dimensional reference pressure generated by a 3 cm×3 cm square piston in nonattenuating media. The excitation frequency is 1 MHz, and the normal particle velocity distribution is uniform across the piston surface. The reference pressure is computed with the fast near-field method. The result is normalized to the maximum pressure amplitude computed in the three-dimensional volume.
FIG. 3
FIG. 3
Simulated pressure generated by a 3 cm×3 cm square piston in nonattenuating media computed by the angular spectrum approach using (a) the spectral propagator without angular restriction, (b) the spectral propagator with angular restriction, and (c) the spatial propagator. The excitation frequency is 1 MHz. All fields are calculated in successive D×D transverse planes (D=9 cm), so the circular convolution errors generated by the spatial propagator are included.
FIG. 4
FIG. 4
Axial plots of the absolute value of the simulated complex pressure. Results are shown for the reference, the angular spectrum approach using the spectral propagator without and with angular restriction, and the spatial propagator.
FIG. 5
FIG. 5
Normalized root mean squared errors for the pressure generated by a uniform normal particle velocity distribution in nonattenuating media. The errors are evaluated in three-dimensional volumes where the lateral dimensions are (a) D×D and (b) L×L with L=D−2a. The markers on the curves indicate the corresponding results shown in Fig. 3.
FIG. 6
FIG. 6
The absolute value of the complex reference pressure generated by a 3 cm×3 cm square piston in attenuating media (α =1 dB/cm/MHz). The excitation frequency is 1 MHz, and the normal velocity distribution is uniform across the piston surface. The reference pressure is computed with the fast near-field method.
FIG. 7
FIG. 7
The absolute value of the simulated complex pressure in attenuating media computed with the angular spectrum approach using (a) the spectral propagator without angular restriction, (b) the spectral propagator with angular restriction, and (c) the spatial propagator. All fields are calculated in successive D×D transverse planes (D=9 cm) and truncated to L×L (L=6 cm), where L=D−2a.
FIG. 8
FIG. 8
Normalized root mean squared errors for the pressure generated in attenuating media (α =1 dB/cm/MHz) by a 3 cm×3 cm uniformly excited square piston. The errors are evaluated in three-dimensional volumes where the lateral dimensions are L×L with L=D−2a. The markers on the curves indicate the corresponding results shown in Fig. 7.
FIG. 9
FIG. 9
The absolute value of the simulated complex pressure in nonattenuating media generated by a 3 cm×3 cm square piston with an apodized normal particle velocity distribution. (a) The reference pressure and (b) the pressure computed by the spectral propagator without angular restriction. The excitation frequency is 1 MHz.
FIG. 10
FIG. 10
Normalized root mean squared errors for the pressure generated in nonattenuating media by a 3 cm×3 cm square piston with an apodized normal particle velocity distribution. The errors are evaluated in three-dimensional volumes where the lateral dimensions are L×L with L=D−2a. The marker on the dotted line indicates the result in Fig. 9(b).
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Goodman JW. Introduction to Fourier Optics. 2nd ed. McGraw-Hill; New York: 1996.
    1. Clement GT, Hynynen K. Field characterization of therapeutic ultrasound phased arrays through forward and backward planar projection. J. Acoust. Soc. Am. 2000;108:441–446. - PubMed
    1. Orofino DP, Pedersen PC. Efficient angular spectrum decomposition of acoustic sources. I. Theory. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 1993;40:238–249. - PubMed
    1. Orofino DP, Pedersen PC. Efficient angular spectrum decomposition of acoustic sources. II results. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 1993;40:250–257. - PubMed
    1. Stepanishen PR, Benjamin KC. Forward and backward projection of acoustic fields using FFT methods. J. Acoust. Soc. Am. 1982;71:803–812. - PubMed

Publication types