A Simple Fusion Method for Image Time Series Based on the Estimation of Image Temporal Validity

Abstract

High-spatial-resolution satellites usually have the constraint of a low temporal frequency, which leads to long periods without information in cloudy areas. Furthermore, low-spatial-resolution satellites have higher revisit cycles. Combining information from high- and low- spatial-resolution satellites is thought a key factor for studies that require dense time series of high-resolution images, e.g., crop monitoring. There are several fusion methods in the bibliography, but they are time-consuming and complicated to implement. Moreover, the local evaluation of the fused images is rarely analyzed. In this paper, we present a simple and fast fusion method based on a weighted average of two input images (H and L), which are weighted by their temporal validity to the image to be fused. The method was applied to two years (2009–2010) of Landsat and MODIS (MODerate Imaging Spectroradiometer) images that were acquired over a cropped area in Brazil. The fusion method was evaluated at global and local scales. The results show that the fused images reproduced reliable crop temporal profiles and correctly delineated the boundaries between two neighboring fields. The greatest advantages of the proposed method are the execution time and ease of use, which allow us to obtain a fused image in less than five minutes.

1. Introduction

Time series of satellite images allow the extraction of vegetation phenology and are thought a key factor in many studies, including vegetation monitoring (crops, forests, etc.) [1], biomass production study [2] and land cover classification [3]. Monitoring agricultural activities is crucial for the assessment of productivity and food supplies, and it requires information that highly varies in space and time [4]. Historically, the crop yield estimation was assessed by local experts and/or statistics. Currently, remote sensing offers spatial information with high spatial and temporal coverage, and though it can be exploited to provide decisive information in agricultural applications.

Natural vegetation and forests phenology is also required for mapping and studying forests ecosystems, the effect of climate changes on forests and the effect of greenhouse gasses and carbon sequestration [5,6,7,8,9]. The use of image time series is also highly valuable for land cover classification purposes because it allows capturing information of the vegetation at different growth stages, which leads to more accurate classifications than by using single images [1,3].

However, in each study case, different spatial resolution images may be required. For forest studies, images with a low spatial resolution (250 m–1 km) may be suitable for obtaining the phenology. For land cover classification and agricultural purposes, higher-spatial-resolution images are desired. In the latter cases, the required spatial resolution depends on the heterogeneity and size of the agricultural parcels in the study area. Generally, spatial resolutions of 10–250 m can be used for land cover classification. Images with spatial resolution of 5–30 m may be more suitable for crop monitoring. Nevertheless, times series of high-spatial-resolution (HR) images have a coarse temporal resolution, whereas low-spatial-resolution (LR) satellites may offer daily information. For example, the MODIS (MODerate Resolution Image Spectroradiometer) sensor offers daily images with a spatial resolution of 250 m–1 km (depending on the spectral band), whereas the Landsat satellite offers information at 30 m spatial resolution with a temporal frequency of 16 days. Moreover, the drawback of low temporal frequency time series is much more evident in areas with important cloud coverage because the presence of clouds can determine missing or inaccurate information for long time periods. Additionally, when using HR image time series one may need to cope with missing data at specific dates (when an observation is necessary), since an image might not to be acquired at the desired time, and with the high economic costs, which are an important constraint, particularly when many images are required.

Fusion or blending methods of image time series allow simulating HR images in dates where only LR images are available; thus, they can be a solution to cope with the above problems. These methods are usually based on rules to combine the information of HR and LR images at different dates. Many existing methods have been defined and applied for the combination of Landsat and MODIS images. A widely used fusion method is the Spatial and Temporal Adaptive Reflectance Fusion Model (STARFM) [10]. This method can be applied using one or two pairs of HR and LR images, and a low-resolution image at the target date (the date of the image that we pretend to obtain). The STARFM has been used to evaluate the gross primary productivity of crops in India by combining Landsat and MODIS images to simulate 46 images in 2009 [11]. In [12], the STARFM was used to complete a time series that allowed improving the classification of tillage/no tillage fields. In [13], it was used to construct a Landsat image time series (2003–2008) to monitor changes in vegetation phenology in Australia.

A modification of the STARFM was developed by [14] and named the Enhanced Spatial and Temporal Adaptive Reflectance Fusion Method (ESTARFM). The ESTARFM requires two pairs of HR and LR images. In [15], the two algorithms (STARFM and ESTARFM) were compared at two different sites. The authors concluded that the ESTARFM outperformed the STARFM in one site, and the STARFM outperformed the ESTARFM in the other site. The main difference between the two sites is the predominance of temporal or spatial variance: the ESTARFM is better for a site where spatial variance is dominant, whereas the STARFM is preferred when temporal variance is dominant.

Fusion methods are usually validated using global statistics, such as the correlation between real images acquired at the same dates when the fused images were simulated, Root Mean Square Error (RMSE), Mean Absolute Deviation (MAD) and Average Absolute Difference (AAD). These statistic parameters provide an indication of the global accuracy; however, the performance at the local scale should also be analyzed.

The objective of this work was to refine and validate a fusion method introduced in [16], in order to have a simple and fast image fusion method that only uses two input images and fuzzy operators. “Simple” indicates that it does not require much input in terms of both data and parameters, and “fast” indicates that it substantially reduces the computational time required to generate a fused image with respect to concurrent methods by achieving at least comparable results to those methods, as described in the validation analysis section. The method was tested in an agricultural area in Brazil, which was mainly covered with Eucalyptus plantations, with MODIS and Landsat images. The method validation and comparison to the ESTARFM were performed at global and local scales.

2. Theoretical Bases

The fusion method was developed based on several desired properties and conditions as defined in our previous work [16]. In the present paper, we refine this method and evaluate its potentialities by emphasizing the settings for its application. The desired condition was to develop a simple method that requires only two input images, one high-resolution image (H) available at any unspecified date and one low-resolution image (L) on the target date when we want to generate a fused high-resolution image (H’). This method should be applied to pairs of satellite images (H and L) with similar spectral configurations (i.e., same spectral bands, atmospheric corrections and viewing angles). In the case the two images have a distinct spectral configuration, first one has to decide which one of the two images has the configuration to be maintained in the fused image, and then one has to normalize the other image before applying the fusion.

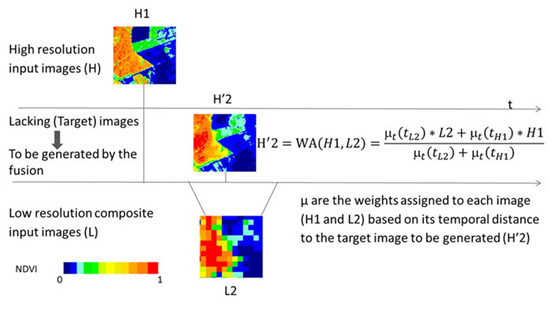
The desired property of the fusion method was to generate the fused image by considering an inverse function of the temporal distances (hereafter called “validity”) between the input images and the target date t. The rationale of using the time validity to weight the contribution of an input image to the fused image is based on the assumption that vegetation covers are affected by gradual changes with time: the closer the date of acquisition of the input image to the target date, the higher should be its “similarity” to the image at the target date. Thus, we weight the input image contribution by an inverse function of its time distance from the target date.

Figure 1 shows a schema of this idea, which includes the graphic representation of the validity degrees (μ). We have two time series: one of high-resolution images (H) taken at dates t_H and one of low/coarse-resolution images (L), which are composite images of several days within a temporal range [t_Lmin, t_Lmax] (t_Lmin and t_Lmax represent the first and last days of the compositing image). The unimodal function of the temporal distances between the input images H and L is a triangular membership function of a fuzzy set defined on the temporal domain of the time series; the central vertex is t and the other two vertices t₀ and t_E are placed before and after t. Therefore, the validity of a timestamp t_H is computed as follows:

$$\begin{array}{l}\text{If} t_{\mathit{0}} \le t_H < t \text{then} {\mu }_t(t_H)=(t_H-{\mathrm{t}}_0)/(t-t_{\mathit{0}})\\ \text{If} t \le t_H < t_E \text{then} {\mu }_t(t_H)=(t_H-t_E)/(t-t_E)\end{array}$$

(1)

Figure 1. Representation of two time series of High- (H2, H4) and Low- (L1, L2, L3, L4) resolution images with distinct timestamps (t_H, t) and temporal density. The black bars represent the membership degrees that define the time validities (μ_t(t_H), μ_t(t_Lmin), μ_t(t_Lmax)) of the images with respect to the target timestamp t. t₀ and t_E are determined from a user-defined parameter t_x.

Figure 1. Representation of two time series of High- (H2, H4) and Low- (L1, L2, L3, L4) resolution images with distinct timestamps (t_H, t) and temporal density. The black bars represent the membership degrees that define the time validities (μ_t(t_H), μ_t(t_Lmin), μ_t(t_Lmax)) of the images with respect to the target timestamp t. t₀ and t_E are determined from a user-defined parameter t_x.

The temporal range [t₀, t_E] can be established based on previous or heuristic data or by training the method using different values. For example, if we know that the scene in the images is almost entirely covered by a Eucalyptus forest with two main seasons, because we know that eucalyptus lose their leaves at the end of the dry season, we can define the time validity of the images that model this variation. In the present case, the temporal range is modulated using a user-defined parameter t_x as follows:

$$\begin{array}{c}{t}_0=\text{min}(t_{Lmin},t_H,t)-t_x\\ t_E=\text{max}(t_{Lmax},t_H,t)+t_x\end{array}$$

(2)

In the experiment reported in this paper, since our objective was to find the best settings of [t₀, t_E] by a training phase, we tested the method with different settings of t_x for a specific region.

For low-resolution composite images, the validity degrees μ_t(t_Lmin) and μ_t(t_Lmax) of their time limits t_Lmin and t_Lmax were computed by replacing t_H with t_Lmin and t_Lmax in Equation (1). Then, the maximum validity is chosen as the validity degree of image L (Equation (3)), which implies that the best validity of the two extremes of the time range of the L image is chosen.

$${\mu }_t(t_L)=\text{max}({\mu }_t(t_{Lmin}), {\mu }_t(t_{Lmax}))$$

(3)

A simple and intuitive fusion function that satisfies the previously stated desired property is a weighted average (Equation (4)) between the L and H images, where the weights are a function that depend on the validities as computed using Equation (2).

$$h^{\prime }=\frac{f({\mu }_t(t_L))*L+f({\mu }_t(t_H))*H}{f({\mu }_t(t_L))+f({\mu }_t(t_H))}$$

(4)

The choice of the function f can be modified based on either a sensitivity analysis that exploits the training data or by stating some hypothesis.

The first simple method is to set the function f as an identity: f(μ_t(t)) = μ_t(t); thus, the equation is directly the weighted average (WA, Equation (5)), which implies that each pixel of the fused image is the weighted average between the pixel at H and the downscaled pixel of the L image. Notice that this weighted average differs from the weighted average where the weights are inversely proportional to the absolute time difference between t and t_H, and t and t_L.

$$h^{\prime }=WA(H,L)=\frac{{\mu }_t(t_L)*L+{\mu }_t(t_H)*H}{{\mu }_t(t_L)+{\mu }_t(t_H)}$$

(5)

A hypothesis can be made if we know a priori that one of the two time series is preferred to the other one. For example, in the present study case, the L image always has a higher validity than the H image; however, because our intention is to obtain an H image, we may want to enhance the weight of the input H image by placing a preference on it. The enhanced weight is defined by a parameter p > 0, representing the preference, which serves to modulate the WA so as to obtain a weighted average with preference (WP, Equation (6)):

$$WP(H,L,p)=\frac{{({\mu }_t(t_L))}^p*L+{({\mu }_t(t_H))}^{1/p}*H}{{({\mu }_t(t_L))}^p+{({\mu }_t(t_H))}^{1/p}} \text{in} \text{which} p > 0$$

(6)

In this function, f(.)^p is a concentrator modifier, i.e., it decreases the weight of the argument when p increases above 1; conversely, when p > 1, f(.)^1/p increases the weight of the argument of the function. Thus, when p > 1 the weight of image H is increased with respect to the weight of image L, which is decreased. The contrary occurs when 0 < p < 1.

The second hypothesis can be made if we want to avoid overestimating or underestimating the pixel values. For example, if our time series correspond to a growing season, we do not want to underestimate the fused values, whereas if we are in a decreasing season, we do not want to overestimate. This is because in the growing season the pixel values representing an indication of the vegetation vigor in a given area are likely to increase, and conversely in a decreasing season. These hypotheses are considered in the method hereafter called WP, whose formulation is as follows (Equations (7) and (8)):

$$\text{Not} \text{overestimating} \text{NOVER} (H, L, p): h^{\prime }(H, L)=min\left(\begin{array}{l}WA(H, L)\\ WP(H, L)\end{array}\right)$$

(7)

$$\text{Not} \text{underestimating} \text{NUNDER} (H, L, p): h^{\prime }(H, L)=max\left(\begin{array}{l}WA(H, L)\\ WP(H, L)\end{array}\right)$$

(8)

The selection between applying NOVER or NUNDER depends on the season identification: growing or decreasing. The season is automatically identified from the date and average NDVI values of each image.

Growing season (NUNDER): t_L < t_H and av.(H) < av.(L) or t_L > t_h and av.(L) > av.(H)

Decreasing season (NOVER): t_L < t_H and av.(H) > av.(L) or t_L > t_h and av.(L) < av.(H)

3. Study Area and Data Used

The study area is located in the Sao Paulo state, southeastern Brazil. In this region, there are an important number of Eucalyptus plantations, which have been studied in [17]. Eucalyptus is a fast-growing crop with rotation cycles of five to seven years. The growth rate is affected by seasonal changes, particularly in the dry season, when the trees are water-limited [17,18].

MODIS and Landsat images were downloaded for 2009 and 2010 to be used in this study. The vegetation indices MODIS product (MOD13Q1) was selected because of the usefulness of vegetation indices for monitoring purposes. MOD13Q1 product offers 16-day composite images with 250 m spatial resolution. As high-resolution images, the Landsat product Surface Reflectance Climate Data Record (CDR) was selected. Landsat CDR provides surface reflectance from Landsat 5 satellite with 30 m spatial resolution and 16 days revisit cycle.

For the MODIS images, 21 images per year of the MOD13Q1 product were available with low cloud coverage. For the Landsat images, only six were available for 2009 (corresponding to the dates 1 February, 22 April, 24 May, 12 August, 25 August, 13 September) and three for 2010 (corresponding to the dates 4 February, 31 August, 3 November). A schema of the available time series is shown in Figure 2. The selected study area is 160 km × 140 km. An example of MODIS and Landsat images over the study area is shown in Figure 3. The same area is zoomed in from the two images respectively to show the spatial-resolution effect; note that in the Landsat images, we can identify the fields, which is not possible in the MODIS images.

Figure 2. Available high- and low-resolution images for the years 2009 and 2010; the dates are expressed in day of year.

Figure 2. Available high- and low-resolution images for the years 2009 and 2010; the dates are expressed in day of year.

Figure 3. NDVI images of the study area: (a) Landsat (acquisition date on 22 April 2009) and (b) MODIS image (composition period: 7 April 2009–22 April 2009). The images are radiometrically normalized.

Figure 3. NDVI images of the study area: (a) Landsat (acquisition date on 22 April 2009) and (b) MODIS image (composition period: 7 April 2009–22 April 2009). The images are radiometrically normalized.

4. Methodology

4.1. Preparation of the Time Series

The first preprocessing step consisted of masking pixels with low quality information because of clouds, shadows or other factors. Both products (MOD13Q1 and CDR) are provided with a quality band, which was used to mask the poor-quality pixels in all images.

Afterwards, to assure the spectral comparability of the images, a normalization procedure was applied. In this case, the Landsat time series was normalized to the MODIS one using the method described in [17]. The normalization method requires that the high-spatial-resolution image is first degraded to the low-spatial-resolution of the MODIS image in order to compute a linear regression between the co-referent pixels of both images, i.e., pixels covering the same area. The degradation was performed using the pixel aggregate method of ENVI software (Exelis Visual Information Solutions, Boulder, CO, USA): this method averages all values of the pixels in the Landsat image which cover a subpart of the area of a MODIS pixel by taking into account their distinct contributions to the area. The equation obtained from the linear regression adjustment between MODIS and Landsat-degraded pixels is the normalization equation, and it relates the pixel radiances of Landsat to MODIS. Therefore, the normalization equation is applied to the Landsat image at its original spatial resolution. The normalization was applied to the red and NIR bands of the Landsat and MOD13Q1 images, and the NDVI was computed from the normalized bands. Successively, the MODIS images were rescaled to the Landsat spatial resolution using a bilinear interpolation method, thus yielding the MODIS and Landsat pixels with the same size. Finally, a subset (Figure 3) was extracted for both time series.

4.2. Fusion Methods

4.2.1. Fusion Methods Based on Temporal Validity

The methods described in section two (WA and WP including NOVER/UNDER) were applied to the available NDVI time series. These methods can be applied with different parameterizations by changing the combination of input images and the temporal range (t_x) in both cases (WA and WP) and by changing the preference (p) in the WP. Preference values greater than 1 will give a larger effect of the input H image on the fused image. Therefore, two experiments were carried on to analyze the effect of the parameters and the combination of input images.

In the first experiment, the temporal range was fixed at t_x = 50, whereas several values of p were examined. Additionally, different combinations of input images were used for each target date.

In the second experiment, a unique combination of input images per target date was used, and the preference value was also set to a fixed value (the input images and preference value that were identified in the previous experiment as leading to the best results). In this case, the temporal range was changed with t_x values varying in 5–200.

These two experiments were performed on the 2009 time series to simulate H images at the dates when we had a Landsat image: 112 (22 April), 144 (25 May), 224 (12 August), 240 (28 August) and 256 (13 September). The existing Landsat image, which was not used in the fusion method, was used for validation. These experiments allowed us to choose the best combination of input images, the best parameter values and the best method. Landsat image 1 January 2009 (32) was not used in experiments 1 and 2 because the MODIS image with timestamp at this date was lacking; therefore, the normalization of the Landsat image was not possible. However, the Landsat image (32) was normalized using the next MODIS image and used in the evaluation at the local scale.

Afterwards, the best method was used to fuse all lacking images over the entire time series (2009–2010). A complete enriched time series was built using the true Landsat images on the dates when they were available and completed with the fused images.

4.2.2. ESTARFM

The ESTARFM method uses two pairs of input images, H and L, which are taken on the same date and one L on the target date. The L images are downscaled to the high spatial resolution. Then, the two pairs of images are independently used to identify similar pixels in a predefined window. Afterwards, a conversion coefficient is obtained between the H and L images from the two pairs of images. The conversion coefficient corresponds to the gain obtained using regression analysis of the previously identified similar pixels. Then, a reflectance value is obtained from each pair of input images and the L image at the target date. Finally, a weighted average is applied by considering three factors: the spectral differences between H and L images on the same date, the temporal differences between the two L images and the spatial distance between similar pixels in the moving window and its central pixel.

The default ESTARFM parameters were used (window size of 51 and 4 classes). The requirement of two pairs of input images limits the possible input combinations. Moreover, because the processing time of this method is long, only one combination of input dates per target was tested. The method was used, as the methods based on the weighted average, to obtain H images on the dates when we had a Landsat image. In this case, the red and NIR band were fused, and the NDVI was subsequently calculated. The validation results were compared to those obtained using the WA and WP methods.

Then, the H time-series 2009–2010 was enriched by simulating the lacking images.

4.3. Validation Analysis

Different fusion methods were compared in terms of the quality of the fused images based on the validation results at global and local scales and in terms of ease of applicability and processing time.

4.3.1. Validation at Global Scale

Since the objective of a fusion method is to simulate a target image at a given date, in order to perform the validation it was necessary to generate fused images at target dates when we had available real images, i.e., true images, acquired at the same dates and with the same spatial resolution of the fused images. The quality of fusion methods is usually assessed on the basis of a pair-wise cross comparison technique, in which the single values of the co-referent pixels in the fused image and in the true image (a real image acquired at the same date of the fused one) are matched so as to allow the computation of their difference and of some global statistics validation measures among the two images. The most usual statistics are: correlation, gain, offset, Root Mean Square Error (RMSE), Mean Absolute Deviation (MAD) and Mean Absolute Deviation in Percentage (MADP). MAD and MAPD are formulated as follows:

$$\text{Mean} \text{Absolute} \text{Deviation}: \text{MAD}=\frac{{\sum }_{i=1}^{\mathrm{N}}|h_i^{\prime }-h_i|}{\mathrm{N}}$$

$$\text{Mean} \text{Absolute} \text{Deviation} \text{in} \text{Percentage}: \text{MADP}=100*\frac{{\sum }_{i=1}^{\mathrm{N}}(|h_i^{\prime }-h_i|/h_i)}{N}$$

where $h_i^{\prime }$ and h_i are the predicted (pixel values in the fused image) and observed (pixel values in the real image) values, respectively, and N is the number of pixels.

This validation procedure was applied to compare different tests in experiments 1 and 2 of the WA and WP methods and to compare with the ESTARFM.

4.3.2. Evaluation at Local Scale

Since global validation can hide local variations that have an important thematic sense, an evaluation procedure at the local scale was developed to analyze the usefulness for monitoring purposes.

The time series from 2009 and 2010 were used (MODIS time series and enriched Landsat time series). The evaluation procedure (Figure 4) consisted of identifying two neighboring fields from the H images, where one pure L pixel could be identified in each field (pixels 1 and 2 in Figure 4). The temporal profile of the pure-resolution pixels was extracted from the MODIS time series. A mixed L pixel was identified in the limit between both fields (pixel 3 in Figure 4). Inside the mixed pixel, some H pixels (grey polygons) were identified as belonging to field 1 (L1a, L1b) and the others as belonging to field 2 (L2a, L2b). The temporal profile of the H pixels was extracted from the enriched Landsat time series. Temporal profile of pixels L1a and L1b should be close to temporal profile of MODIS pixel 1 because they belong to the same field. Similarly, pixels L2a and L2b should have a close temporal profile to MODIS pixel 2. Moreover, if the fields are different, the profiles of pixels belonging to field 1 (L1a and L1b) should be different from those of field 2 (L2a, L2b). If the temporal profiles of the fused images behave like that, this would prove a good performance of the fused images for monitoring purposes.

Figure 4. Diagram of the validation procedure at the local scale. Two neighboring fields (red boxes) are identified. The blue squares represent coarse-resolution pixels: MODIS pixels 1 and 2 in the center of fields 1 and 2 represent pure coarse-resolution pixels. MODIS pixel 3, which is identified in the limit between both fields, represents a mixed coarse-resolution pixel. The grey polygons in pixel 3 represent H pixels: two of field 1 and two of field 2.

Figure 4. Diagram of the validation procedure at the local scale. Two neighboring fields (red boxes) are identified. The blue squares represent coarse-resolution pixels: MODIS pixels 1 and 2 in the center of fields 1 and 2 represent pure coarse-resolution pixels. MODIS pixel 3, which is identified in the limit between both fields, represents a mixed coarse-resolution pixel. The grey polygons in pixel 3 represent H pixels: two of field 1 and two of field 2.

5. Results

5.1. Parameterization of the WA and WP Fusion Methods

Different parameterizations were analyzed in experiments 1 and 2. The results of the experiments were compared based on global validation indices. Two fusion methods based on the temporal validity were applied to simulate H images on dates when a real image was available (target image). Then, the target image was used to validate the fused image. The following statistics were obtained from the fused and target images: correlation (R), gain (a), offset (b), RMSE and MADP.

5.1.1. Experiment 1

In the first experiment, different combinations of input images and different preference values were tested. The temporal range was set at t_x = 50. Regarding the input image dates, it is expected that selecting the closest H image leads to better results. However, the selection of the L image is not as evident because the target dates correspond to the last date of the composition of the L image. In some cases, it may be better to select the L that includes the target date, whereas in other cases, it may be better to select the next L image. For example, to simulate image 144 (Figure 5), if we took the H image on date 112 as L, we could select image 137 (which corresponds to the period 129–144 and thus corresponds to the target date) or take the next image, 153 (corresponding to the period 145–160). Several tests were performed accordingly and are shown in Table 1.

Table 1. Results of the validation of the WA and WP fusion methods for six target images using different input images and preferences for 2009. The image dates are expressed as day of year (DoY). The following statistics where obtained from the fused and target images: correlation (R), gain (a), offset (b), RMSE and MADP. The results that correspond to the best combination of input images and the best method are marked in bold.

	Target	112			144							224			240		256
	H	32	32	144	32	32	112	112	224	240	256	144	144	256	144	144	144	144	224	224
	L	97–112	113–128	97–112	129–255	145–160	129–144	145–160	129–144	129–144	129–144	209–224	225–240	209–224	225–240	241–256	241–256	257–272	241–256	257–272
	Dist(t-th)	80	80	−32	112	112	32	32	−80	−96	−112	80	80	−32	96	96	112	112	32	32
	Dist(t-tLmin)	15	−1	15	15	−1	15	−1	15	15	15	15	−1	15	15	−1	15	−1	15	−1
	R (H,Target)	0.63	0.63	0.79	0.59	0.59	0.79	0.79	0.64	0.62	0.58	0.64	0.64	0.84	0.62	0.62	0.58	0.58	0.84	0.84
	R(L,Target)	0.75	0.76	0.75	0.75	0.78	0.75	0.77	0.75	0.75	0.75	0.78	0.79	0.78	0.78	0.79	0.77	0.73	0.77	0.73
WA	R(H’,Target)	0.79	0.80	0.86	0.78	0.80	0.84	0.87	0.80	0.80	0.79	0.82	0.83	0.88	0.81	0.83	0.79	0.78	0.86	0.87
	a	0.66	0.68	0.82	0.59	0.63	0.70	0.74	0.66	0.67	0.63	0.72	0.73	0.79	0.74	0.74	0.68	0.66	0.80	0.78
	b	0.26	0.23	0.12	0.31	0.27	0.23	0.19	0.21	0.20	0.24	0.19	0.19	0.13	0.19	0.20	0.22	0.25	0.13	0.15
	RMSE	0.08	0.07	0.06	0.09	0.08	0.08	0.07	0.08	0.08	0.08	0.08	0.08	0.07	0.09	0.09	0.09	0.10	0.07	0.07
	MAPD	8.84	8.65	7.41	11.37	10.43	9.45	8.50	10.33	10.54	10.87	12.66	12.27	9.70	13.41	13.63	13.16	14.73	9.97	10.37
WP, p = 1.5	R( H’,Target)	0.79	0.80	0.86	0.78	0.81	0.84	0.87	0.80	0.79	0.78	0.81	0.82	0.89	0.81	0.82	0.79	0.78	0.86	0.87
	a	0.66	0.68	0.82	0.58	0.63	0.70	0.74	0.66	0.67	0.63	0.72	0.72	0.79	0.73	0.73	0.68	0.66	0.80	0.79
	b	0.26	0.23	0.12	0.31	0.27	0.23	0.19	0.20	0.20	0.23	0.20	0.19	0.13	0.19	0.20	0.22	0.25	0.13	0.15
	RMSE	0.08	0.07	0.06	0.09	0.08	0.08	0.07	0.08	0.08	0.09	0.09	0.08	0.07	0.09	0.09	0.09	0.09	0.07	0.07
	MAPD	8.80	8.65	7.38	11.34	10.43	9.41	8.47	10.39	10.65	11.00	12.75	12.38	9.58	13.48	13.66	13.17	14.59	9.86	10.18
WP, p = 2	R( H’,Target)	0.79	0.80	0.86	0.78	0.81	0.84	0.87	0.80	0.79	0.78	0.81	0.82	0.89	0.81	0.82	0.79	0.78	0.86	0.87
	a	0.66	0.67	0.82	0.58	0.62	0.70	0.74	0.67	0.67	0.63	0.71	0.71	0.79	0.73	0.73	0.68	0.66	0.80	0.79
	b	0.26	0.23	0.12	0.31	0.27	0.23	0.19	0.20	0.19	0.23	0.20	0.19	0.13	0.19	0.20	0.22	0.24	0.12	0.14
	RMSE	0.08	0.07	0.06	0.09	0.08	0.08	0.07	0.08	0.09	0.09	0.09	0.08	0.07	0.09	0.09	0.09	0.09	0.07	0.07
	MAPD	8.79	8.65	7.36	11.33	10.43	9.40	8.45	10.43	10.73	11.09	12.79	12.44	9.53	13.51	13.67	13.16	14.51	9.81	10.08

Table 1. Results of the validation of the WA and WP fusion methods for six target images using different input images and preferences for 2009. The image dates are expressed as day of year (DoY). The following statistics where obtained from the fused and target images: correlation (R), gain (a), offset (b), RMSE and MADP. The results that correspond to the best combination of input images and the best method are marked in bold.

	Target	112			144							224			240		256
	H	32	32	144	32	32	112	112	224	240	256	144	144	256	144	144	144	144	224	224
	L	97–112	113–128	97–112	129–255	145–160	129–144	145–160	129–144	129–144	129–144	209–224	225–240	209–224	225–240	241–256	241–256	257–272	241–256	257–272
	Dist(t-th)	80	80	−32	112	112	32	32	−80	−96	−112	80	80	−32	96	96	112	112	32	32
	Dist(t-tLmin)	15	−1	15	15	−1	15	−1	15	15	15	15	−1	15	15	−1	15	−1	15	−1
	R (H,Target)	0.63	0.63	0.79	0.59	0.59	0.79	0.79	0.64	0.62	0.58	0.64	0.64	0.84	0.62	0.62	0.58	0.58	0.84	0.84
	R(L,Target)	0.75	0.76	0.75	0.75	0.78	0.75	0.77	0.75	0.75	0.75	0.78	0.79	0.78	0.78	0.79	0.77	0.73	0.77	0.73
WA	R(H’,Target)	0.79	0.80	0.86	0.78	0.80	0.84	0.87	0.80	0.80	0.79	0.82	0.83	0.88	0.81	0.83	0.79	0.78	0.86	0.87
	a	0.66	0.68	0.82	0.59	0.63	0.70	0.74	0.66	0.67	0.63	0.72	0.73	0.79	0.74	0.74	0.68	0.66	0.80	0.78
	b	0.26	0.23	0.12	0.31	0.27	0.23	0.19	0.21	0.20	0.24	0.19	0.19	0.13	0.19	0.20	0.22	0.25	0.13	0.15
	RMSE	0.08	0.07	0.06	0.09	0.08	0.08	0.07	0.08	0.08	0.08	0.08	0.08	0.07	0.09	0.09	0.09	0.10	0.07	0.07
	MAPD	8.84	8.65	7.41	11.37	10.43	9.45	8.50	10.33	10.54	10.87	12.66	12.27	9.70	13.41	13.63	13.16	14.73	9.97	10.37
WP, p = 1.5	R( H’,Target)	0.79	0.80	0.86	0.78	0.81	0.84	0.87	0.80	0.79	0.78	0.81	0.82	0.89	0.81	0.82	0.79	0.78	0.86	0.87
	a	0.66	0.68	0.82	0.58	0.63	0.70	0.74	0.66	0.67	0.63	0.72	0.72	0.79	0.73	0.73	0.68	0.66	0.80	0.79
	b	0.26	0.23	0.12	0.31	0.27	0.23	0.19	0.20	0.20	0.23	0.20	0.19	0.13	0.19	0.20	0.22	0.25	0.13	0.15
	RMSE	0.08	0.07	0.06	0.09	0.08	0.08	0.07	0.08	0.08	0.09	0.09	0.08	0.07	0.09	0.09	0.09	0.09	0.07	0.07
	MAPD	8.80	8.65	7.38	11.34	10.43	9.41	8.47	10.39	10.65	11.00	12.75	12.38	9.58	13.48	13.66	13.17	14.59	9.86	10.18
WP, p = 2	R( H’,Target)	0.79	0.80	0.86	0.78	0.81	0.84	0.87	0.80	0.79	0.78	0.81	0.82	0.89	0.81	0.82	0.79	0.78	0.86	0.87
	a	0.66	0.67	0.82	0.58	0.62	0.70	0.74	0.67	0.67	0.63	0.71	0.71	0.79	0.73	0.73	0.68	0.66	0.80	0.79
	b	0.26	0.23	0.12	0.31	0.27	0.23	0.19	0.20	0.19	0.23	0.20	0.19	0.13	0.19	0.20	0.22	0.24	0.12	0.14
	RMSE	0.08	0.07	0.06	0.09	0.08	0.08	0.07	0.08	0.09	0.09	0.09	0.08	0.07	0.09	0.09	0.09	0.09	0.07	0.07
	MAPD	8.79	8.65	7.36	11.33	10.43	9.40	8.45	10.43	10.73	11.09	12.79	12.44	9.53	13.51	13.67	13.16	14.51	9.81	10.08

Figure 5. Example of some possible combinations of input images to simulate image 144. When selecting the input high-resolution 112, two possible low-resolution images can be used as the input: 137 and 153 because timestamp 144 is in the middle of both.

Figure 5. Example of some possible combinations of input images to simulate image 144. When selecting the input high-resolution 112, two possible low-resolution images can be used as the input: 137 and 153 because timestamp 144 is in the middle of both.

The results obtained from the fusion methods based on the temporal validity are presented in Table 1. In some cases, the correlation of the input H image and the target image was particularly high (higher than the correlation between the target and the fused image). In those cases, a notably high correlation between two consecutive H images in a time series indicates that minimum changes occurred between the two dates. Thus, in such cases, we consider that computing a fused image on that date is not practical. For simplicity, these results are not included in the table.

By comparing the methods WA and WP, we observed slightly better results when using the second one, particularly with a preference value of p = 2. Regarding the input dates selection, as expected the use of closer H images leads to better results in all cases. The selection of the L can differ, for example in the case of simulating image 144, we obtained better results when taking the next L image, 153 (Table 1), possibly because of the proximity of the target date to both MODIS images 137 and 153. This result occurs when the input H image had a lower timestamp than the target image; otherwise, better results were obtained when we used the L image that corresponded to the timestamp of the target image.

5.1.2. Experiment 2

In this second experiment, the methods WA and WP with p = 2 were used to analyze the effect of t_x. For each target date, the best combination of input images was selected from the results in Table 1. t_x was varied between 5 and 200. The results of the correlation and the MADP are shown in Figure 6. Augmenting the temporal range [t₀, t_E] leads to closer validities of the H and L images. When the H image is not too far, we expect to obtain better accuracies when augmenting this range. In Figure 6, we observe that the correlation generally increases at the beginning and stabilizes after a certain value, which is consistent with the previous hypothesis. In contrast, in the case of the MADP, it decreases before stabilizing. However, there is a case where the performance is slightly different, and instead of stabilizing, the correlation begins to decrease, and the MADP begins to increase. This is case of the target date 240, where the input H and the target are far away in time (there is a difference of 96 days). A higher range usually provides closer validities between the H and L; however, when the H is far, we should give lower validity to this image; otherwise, the fusion method leads to slightly lower accuracies.

5.2. Comparison with the ESTARFM Method

The ESTARFM method was also applied to simulate the images that corresponded to identical dates as the previous methods. Because this method requires two input pairs of images, the possibilities of input combinations were significantly lower, and only one combination per target date was tested. Moreover, the processing time of this method was extremely long (approximately five hours versus less than five minutes of the proposed methods). The ESTARFM results were compared to the WA and WP with p = 2 and t_x = 100. The input images are those marked in bold in Table 1. The results of the three methods are shown in Table 2. We observe that better correlation and errors (RMSE and MADP) were always obtained when we used the WA and WP methods. Contrarily, the gain and offset were always better with the ESTARFM method. This result may point at the presence of some outliers when using the ESTARFM. For the WP and WA methods, identical or notably similar results are observed; therefore, because of the simpler formulation of the WA method, we chose this method in the following local evaluation analysis.

Figure 6. Validation results (R and MADP) of the proposed fusion methods for different target images by modifying the temporal range: (a) WA and (b) WP.

Figure 6. Validation results (R and MADP) of the proposed fusion methods for different target images by modifying the temporal range: (a) WA and (b) WP.

5.3. Local Evaluation

For monitoring and classification purposes, first, the fields must be correctly identified, and secondly, there must be accurate reflectance or NDVI values. To analyze the usefulness of the fused images with these purposes, the methodology described in Figure 4 was applied. Two neighboring Eucalyptus fields, which were harvested on different dates of 2009, were identified and selected for the present analysis. The presence of the harvests allows us to analyze the usefulness of the enriched time series to detect the harvest date, whereas the use of a two-year time series allows us to analyze the culture monitoring at different seasons and years. The selected fields and pixels are shown in Figure 7. A pure L pixel was identified at the center of each field, and their temporal profiles were extracted from the MODIS time series. Afterwards, four mixed L pixels (black polygons) were identified in the limit between both fields; in each mix L pixel, several H pixels were identified inside each field. The temporal profiles of the pure L and H pixels were obtained from the MODIS and the enriched time series, respectively. For H pixels, the average and standard deviation of the pixels in each field were obtained. The results are shown in Figure 8. Figure 8a,b represent fields A and B, respectively. The temporal profiles of the MODIS images are consistent with the enriched time series with the two fusion methods, particularly in field B. Field A was more heterogeneous than field B, and so the coarse-resolution pixel is possibly more heterogeneous than that in field B. However, an underestimation is frequently observed in the enriched Landsat time series, including the real Landsat images, which shows the difference in spectral response between both satellites and the importance of normalization, which is not perfectly achieved in this case.

Table 2. Comparison of the global validation results of the WP and ESTARFM methods in terms of the correlation (R), gain (a), offset (b), RMSE and MADP.

Target	Method	R	a	b	RMSE	MADP
112	WP	0.86	0.82	0.12	0.06	7.4
	WA	0.86	0.82	0.12	0.06	7.4
	ESTARFM	0.84	0.91	0.05	0.07	7.3
144	WP	0.87	0.74	0.19	0.07	8.5
	WA	0.87	0.74	0.19	0.07	8.5
	ESTARFM	0.83	0.83	0.12	0.08	8.8
224	WP	0.89	0.79	0.13	0.07	9.5
	WA	0.88	0.79	0.13	0.07	9.7
	ESTARFM	0.75	0.82	0.13	0.10	14.0
240	WP	0.82	0.73	0.20	0.09	13.7
	WA	0.83	0.74	0.20	0.09	13.6
	ESTARFM	0.75	0.82	0.13	0.10	14.6
256	WP	0.86	0.80	0.12	0.07	9.8
	WA	0.86	0.80	0.13	0.07	10.0
	ESTARFM	0.86	0.93	0.05	0.07	9.9

Table 2. Comparison of the global validation results of the WP and ESTARFM methods in terms of the correlation (R), gain (a), offset (b), RMSE and MADP.

Target	Method	R	a	b	RMSE	MADP
112	WP	0.86	0.82	0.12	0.06	7.4
	WA	0.86	0.82	0.12	0.06	7.4
	ESTARFM	0.84	0.91	0.05	0.07	7.3
144	WP	0.87	0.74	0.19	0.07	8.5
	WA	0.87	0.74	0.19	0.07	8.5
	ESTARFM	0.83	0.83	0.12	0.08	8.8
224	WP	0.89	0.79	0.13	0.07	9.5
	WA	0.88	0.79	0.13	0.07	9.7
	ESTARFM	0.75	0.82	0.13	0.10	14.0
240	WP	0.82	0.73	0.20	0.09	13.7
	WA	0.83	0.74	0.20	0.09	13.6
	ESTARFM	0.75	0.82	0.13	0.10	14.6
256	WP	0.86	0.80	0.12	0.07	9.8
	WA	0.86	0.80	0.13	0.07	10.0
	ESTARFM	0.86	0.93	0.05	0.07	9.9

The WA enriched time series presented a higher homogeneity of the pixels in both fields than the ESTARFM method, where higher standard deviations were observed.

When a harvest is finished, the NDVI values suffer of an important drop between the day before and after the harvest, as observed in the MODIS time series where the NDVI value decreased from 0.75 to 0.4 in field B. In the case of the enriched H time series, the precise harvest date was difficult to identify in any of the two fusion methods because the NDVI value decreased monotonously instead of abruptly. Some uncertainty will always be present. Nevertheless, one potential advantage of the proposed method is that by knowing in advance the date of the harvest; one could define the membership function in Equation1 modeling the temporal validity of the input images more accurately. The approach could be well suited to incorporate knowledge on the dynamics of the observed vegetation.

Figure 7. Eucalyptus fields A and B selected for the validation at the local scale. The big blue and red polygons represent pure coarse-resolution pixels in two different fields. The black polygons represent mix coarse-pixels in the limit between both fields. The red and blue polygons inside the mix coarse-pixels represent high-resolution pixels that correspond to field A (red) and field B (blue).

Figure 7. Eucalyptus fields A and B selected for the validation at the local scale. The big blue and red polygons represent pure coarse-resolution pixels in two different fields. The black polygons represent mix coarse-pixels in the limit between both fields. The red and blue polygons inside the mix coarse-pixels represent high-resolution pixels that correspond to field A (red) and field B (blue).

Moreover, it can be observed that the profiles obtained from the enriched time series are different for the two fields, which proves the usefulness of the fused images for classification purposes.

In Figure 9, two examples of the original and fused images are shown, which correspond to fields A and B. On the first date, we observed that field A was harvested, whereas in the second image, both fields were harvested. Both fused images could correctly identify the boundary between the two analyzed fields, whereas this boundary was not identifiable in the MODIS image. In the case of 24 May, both fused images show similar values to the original one; however, in the second one (28 August), the ESTARFM presents important errors in field B, which is not the case with the WA method. This is an example of the outliers’ problem in the ESTARFM, which leads to higher error values. We believe that this problem is due to the fact of using two input H images, which obligates to take images that are far in time.

These results show that the enriched H time series with the WA method are highly valuable for classification purposes (they allow the identification of the field limits), and they are also valuable for vegetation monitoring (the temporal profile is well achieved). Moreover, the WA method presents two important advantages compared to the ESTARFM: the requirement of only two input images (one H image and one L image); the processing time, which is approximately five minutes for a nearly entire Landsat image in comparison to approximately five hours with the ESTARFM. Furthermore, because of its simplicity, the WA method offers a higher flexibility for choosing the input images, particularly when there are cloudy images on the desired dates.

Figure 8. Temporal profiles obtained for the pure coarse-resolution pixel and the average values of the pixels in (a) field A and (b) field B. Temporal profiles of the high-resolution pixels are obtained from the enriched time series using the WP and ESTARFM methods.

Figure 8. Temporal profiles obtained for the pure coarse-resolution pixel and the average values of the pixels in (a) field A and (b) field B. Temporal profiles of the high-resolution pixels are obtained from the enriched time series using the WP and ESTARFM methods.

Figure 9. Example of original (Landsat and MODIS) and fused (ESTARFM and WA) images for two dates of 2009. MODIS pure (red) and mixed (white) pixels that were used to obtain the temporal profiles are represented.

Figure 9. Example of original (Landsat and MODIS) and fused (ESTARFM and WA) images for two dates of 2009. MODIS pure (red) and mixed (white) pixels that were used to obtain the temporal profiles are represented.

In the case of study, the H images were simulated using the closest Landsat image as the high-resolution input; however, when this image is taken after the target date, the identification of harvests will be difficult. Using an input Landsat image before the target date will minimize this problem; however, if the input and target dates are far away, the global results will worsen. This result should be considered when selecting the input images depending on the objectives of the study.

6. Discussion

Fusion methods are very useful for completing time series of high-resolution images. Several methods already exist but are complicated and time consuming. We have presented here a simple and fast fusion method; simple because it only needs two input images and a simple formulation that makes it a fast method. Its main characteristics is the ability to model the heuristic knowledge of the crop modeling dynamics by defining a time validity degree for each input image at a target date when one wants to generate a fused image. The time validity is obtained in a temporal range that is user-selected. Although in this case we have performed a test for selecting the temporal range, this approach may be suitable for classified images in order to obtained enriched time series where the crop stages can be monitored. In this case an expert could define the time validity of each pixel in the image depending on the crop type present in the area. Further work will be performed to analyze the usefulness of the enriched time series for crop-monitoring purposes such as crop stage identification, on the line of the initial experiments done by the authors in [19].

Moreover the method has certain limitations. The major limitation may be the need of a normalization procedure between the high- and low-resolution images being used. This procedure is needed because the spectral bands of both satellites may differ, also the atmospheric correction performed to the images from both satellites could be different and have an influence in the reflectivities captured by them. In order to correct these perturbations, we have applied here a simple normalization procedure, which relates the spectral reflectivities (in the red and NIR bands) of the Landsat images to the MODIS ones by linear regression; though we apply the normalization equation to the Landsat images to obtain comparable reflectivities to MODIS. The evaluation at local scale has shown that there are still some differences between the Landsat (normalized) and the MODIS reflectivities, so one perspective of this work will be enhancing the normalization procedure and we expect this will enhance the results of the fusion method. Moreover, although the ESTARFM does not require this normalization procedure, we have checked that better results are obtained when the input images are normalized.

The comparison between ESTARFM and WA lead to similar results, lower errors were generally obtained with WA, but visual inspection showed that in ESTARFM structures seemed better defined; however there were important local errors using ESTARFM, probably due to the need of two high resolution images as input, this force to use images that are far away in time. Because WA was applied to fuse NDVI images and ESTARFM to fuse red and NIR bands, some tentative experiments have been carried out to compare the WA method with ESTARFM method where both are directly applied to the spectral bands as input pixel values. A validation on the 5 Landsat images of 2009 (see Table 3) lead to similar results to those presented previously by applying the proposed fusion to the NDVI images, thus providing promising results which deserve confirmation by consistent and thorough experiments.

A major problem when applying fusion methods is the perfect co-registration of the Landsat and MODIS images, in this work we have paid attention to that problem, but only by visual inspection, although the high correlation values obtained from the normalization equation makes us think that they are well co-register. However we will consider in future works analyzing this problem in detail.

Also, in the future we intend to apply the WA method to other combinations of satellite images, and also consider adapting the method to thermal bands.

Table 3. Comparison of the NDVI global validation results of the WA applied to NDVI pixels and the WA applied to red and NIR in terms of the correlation (R), gain (a), offset (b), RMSE and MADP.

Target	Method	R	a	b	RMSE	MADP
112	WA_NDVI	0.86	0.82	0.12	0.06	7.4
	WA_reflect	0.86	0.82	0.12	0.06	7.4
144	WA_NDVI	0.87	0.74	0.19	0.07	8.5
	WA_reflect	0.86	0.73	0.19	0.07	8.6
224	WA_NDVI	0.88	0.79	0.13	0.07	9.7
	WA_reflect	0.89	0.80	0.12	0.07	9.5
240	WA_NDVI	0.83	0.74	0.20	0.09	13.6
	WA_reflect	0.82	0.73	0.20	0.09	13.8
256	WA_NDVI	0.86	0.80	0.13	0.07	10.0
	WA_reflect	0.86	0.80	0.13	0.07	10.0

Table 3. Comparison of the NDVI global validation results of the WA applied to NDVI pixels and the WA applied to red and NIR in terms of the correlation (R), gain (a), offset (b), RMSE and MADP.

Target	Method	R	a	b	RMSE	MADP
112	WA_NDVI	0.86	0.82	0.12	0.06	7.4
	WA_reflect	0.86	0.82	0.12	0.06	7.4
144	WA_NDVI	0.87	0.74	0.19	0.07	8.5
	WA_reflect	0.86	0.73	0.19	0.07	8.6
224	WA_NDVI	0.88	0.79	0.13	0.07	9.7
	WA_reflect	0.89	0.80	0.12	0.07	9.5
240	WA_NDVI	0.83	0.74	0.20	0.09	13.6
	WA_reflect	0.82	0.73	0.20	0.09	13.8
256	WA_NDVI	0.86	0.80	0.13	0.07	10.0
	WA_reflect	0.86	0.80	0.13	0.07	10.0

7. Conclusions

The purpose of this paper was to refine a simple and fast fusion method. This method was designed to fuse Landsat and MODIS images, although it can be applied to other pairs of high- and low-resolution images. For this method, only two input images are required. The resulting fused image is based on the weighted average (WA) of the two input images. The weight assigned to each image depends on its temporal distance to the target date.

A global validation of the results (fused images) obtained by the simple fusion WA-method was performed using five Landsat images acquired in 2009 over the Sao Paulo region of Brazil. The global validation consists in computing statistical indices between NDVI estimated from target and fused images. The validation results of our simple fusion method were compared to those obtained using a more complex fusion method, the ESTARFM (Enhanced Spatio Temporal Fusion Method). The global validation of the two fusion methods showed good performance, with higher correlations and lower errors (RMSE and MADP) between the target image and the fused image obtained using the proposed WA-method. The RMSE varied between 0.07 and 0.1, and the MADP between 7% and 15% in terms of NDVI. Global validation procedures can hide local errors due to disagreements between fused and reference images. Therefore, in addition to the global validation, an evaluation at local scale was performed using a two-year time series of Landsat and MODIS images. The evaluation at local scale aimed to check the usefulness of the fused images for field delineation and vegetation monitoring. This local evaluation was based on temporal profiles of NDVI. Good results were obtained by comparing temporal profiles extracted from fused images with both methods to a reference temporal profile. However, the WA method led to cleaner results with lower deviations and lower aberrant pixels. Local evaluation is not usually analyzed when validating fusion methods. We have performed a simple evaluation procedure, however this evaluation is limited and further work should be performed for evaluating fusion methods at local scale.

The constraint of the WA method is that a normalization of the input images has to be performed before applying the fusion in order to have radiometrically comparable high and low resolution images. The normalization is not a necessary step in the ESTARFM method although we verified that better results were also obtained when the input images were normalized. However, the evaluation at local scale showed that the normalization procedure applied did not lead to perfect agreement between the high and low resolution images. Though, further work will focus on normalization procedures, since an enhancement of this step would enhance the results of the fusion methods.

To summarize the main achievements, the main advantage of the WA method is its ease of use (only two input images are required), low processing time (less than 5 minutes), and good results.