Analysis and Simulation on Imaging Performance of Backward and Forward Bistatic Synthetic Aperture Radar
Abstract
:1. Introduction
2. Model and Methods in Analyzing Geometric Properties and Related Power Considerations
2.1. Imaging Geometry and Signal Model
2.2. Range Resolution and Azimuth Resolution
2.3. Bistatic Range History
2.4. Bistatic Signal to Noise Ratio (SNR)
2.5. Back-Projection Algorithm
3. Results and Discussion
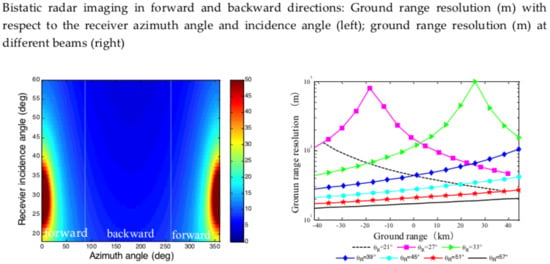
3.1. Imaging Property of Backward and Forward Bistatic SAR
3.2. Power Considerations of Backward and Forward Bistatic SAR
3.3. Chaos Particle Swarm Optimization
- (1)
- Initialize a vector each component using a random number in the range [0, 1] and produce m-D chaos queues by 2N iteration of Logistic equation.
- (2)
- Map the chaos queues into the decision space of the parameters according the following equation to obtain 2N initialized positions
- (3)
- Calculate the fitness values of the vectors using the fitness function and select the best N solutions as the initial positions of N particles.
3.4. Simulation and Results
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Krieger, G.; Hajnsek, I.; Papathanassiou, K.P.; Younis, M.; Moreira, A. Interferometric synthetic aperture radar (SAR) missions employing formation flying. Proc. IEEE 2010, 98, 816–843. [Google Scholar] [CrossRef] [Green Version]
- Erten, E.; Rossi, C.; Yuzugullu, O. Polarization impact in tandem-X data over vertical-oriented vegetation: The paddy-rice case study. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1501–1505. [Google Scholar] [CrossRef]
- Yang, X.F.; Du, Y.L.; Li, Z.W.; Chen, K.S. Investigation of bistatic radar scattering from sea surfaces with breaking waves. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 1502–1503. [Google Scholar]
- Moreira, A.; Gerhard, K.; Hajnsek, I.; Papathanassiou, K.; Younis, M.; Dekker, P.L.; Huber, S.; Villano, M.; Pardini, M.; Michael, E.; et al. Tandem-L: A highly innovative bistatic SAR mission for global observation of dynamic processes on the Earth’s surface. IEEE Geosci. Remote Sens. Mag. 2015, 3, 8–23. [Google Scholar] [CrossRef]
- Guerriero, L.; Pierdicca, N.; Pulvirenti, L.; Ferrazzoli, P. Use of Satellite Radar Bistatic Measurements for Crop Monitoring: A Simulation Study on Corn Fields. Remote Sens. 2013, 5, 864–890. [Google Scholar] [CrossRef] [Green Version]
- Zeng, J.Y.; Chen, K.S. Theoretical Study of Global Sensitivity Analysis of L-band Radar Bistatic Scattering for Soil Moisture Retrieval. IEEE Geosci. Remote Sens. Lett. 2018, 1–5. [Google Scholar] [CrossRef]
- Fernandez, P.D.; Cantalloube, H.; Vaizan, B.; Krieger, G.; Horn, R.; Wendler, M.; Giroux, V. ONERA-DLR bistatic SAR campaign: Planning, data acquistiton, and first analysis of bistatic scattering behaviour of natural and urban targets. IEE Proc. Radar Sonar Navig. 2006, 153, 214–223. [Google Scholar] [CrossRef]
- Cardillo, G.P. On the use of the gradient to determine bistatic SAR resolution. In Proceedings of the Antennas and Propagation Society International Symposium, Dallas, TX, USA, 7–11 May 1990; pp. 1032–1035. [Google Scholar]
- Zeng, T.; Cherniakov, M.; Long, T. Generalized approach to resolution analysis in BSAR. IEEE Trans. Aerosp. Electron. Syst. 2005, 41, 461–474. [Google Scholar] [CrossRef]
- Ender, J.H.G. The meaning of k-space for classical and advanced SAR-techniques. In Proceedings of the Second International Symposium Physics in Signal & Image Processing (PSIP’2001), Marseille, France, 23–24 January 2001. [Google Scholar]
- Moccia, A.; Renga, A. Spatial resolution of bistatic synthetic aperture radar: Impact of acquisition geometry on imaging performance. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3487–3503. [Google Scholar] [CrossRef]
- Jiang, Y.; Wang, Z. Analysis for Resolution of Bistatic SAR Configuration with Geosynchronous Transmitter and UAV Receiver. Int. J. Antennas Propag. 2013, 6, 245–253. [Google Scholar] [CrossRef]
- Sun, Z.C.; Wu, J.J.; Pei, J.F.; Li, Z.Y.; Huang, Y.L.; Yang, J.Y. Inclined geosynchronous spaceborne—Airborne bistatic sar: Performance analysis and mission design. IEEE Trans. Geosci. Remote Sens. 2016, 54, 343–357. [Google Scholar] [CrossRef]
- Wang, R.; Deng, Y.K.; Loffeld, O.; Nies, H.; Walterscheid, I.; Espeter, T.; Klare, J.; Ender, J.H.G. Processing the azimuth-variant bistatic SAR data by using monostatic imaging algorithms based on two-dimensional principle of stationary phase. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3504–3520. [Google Scholar] [CrossRef]
- Zeng, T.; Liu, F.; Hu, C.; Long, T. Image formation algorithm for asymmetric bistatic sar systems with a fixed receiver. IEEE Trans. Geosci. Remote Sens. 2012, 50, 4684–4698. [Google Scholar] [CrossRef]
- Li, D.; Wang, W.; Liu, H.Q.; Cao, H.L.; Lin, H. Focusing highly squinted Azimuth variant Bistatic SAR. IEEE Trans. Aerosp. Electron. Syst. 2017, 52, 2715–2730. [Google Scholar] [CrossRef]
- Walterscheid, I.; Ender, J.H.G.; Brenner, A.R.; Loffeld, O. Bistatic sar processing and experiments. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2710–2717. [Google Scholar] [CrossRef]
- Cassola, M.R.; Prats, P.; Krieger, G.; Moreira, A. Efficient time-domain image formation with precise topography accommodation for general bistatic SAR configurations. IEEE Trans. Aerosp. Electron. Syst. 2011, 47, 2949–2966. [Google Scholar] [CrossRef] [Green Version]
- Shao, Y.F.; Wang, R.; Deng, Y.K.; Liu, Y.; Chen, R.; Liu, G.; Loffeld, O. Fast backprojection algorithm for bistatic SAR imaging. IEEE Geosci. Remote Sens. Lett. 2013, 10, 1080–1084. [Google Scholar] [CrossRef]
- Vu, V.T.; Pettersson, M.I. Fast backprojection algorithms based on subapertures and local polar coordinates for general bistatic airborne sar systems. IEEE Trans. Geosci. Remote Sens. 2016, 54, 2706–2712. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, Y.Y.; Li, Z.F.; Suo, Z.Y.; Fang, C.; Chen, J.L. High-resolution wide-swath imaging of spaceborne multichannel bistatic SAR with inclined geosynchronous illuminator. IEEE Geosci. Remote Sens. Lett. 2017, 14, 2380–2384. [Google Scholar] [CrossRef]
- Gebert, N.; Dominguez, B.C.; Davidson, M.W.J.; Martin, M.D.; Silvestrin, P. SAOCOM-CS—A passive companion to SAOCOM for single-pass L-band SAR interferometry. In Proceedings of the 2014 10th European Conference on Synthetic Aperture Radar (EUSAR), Berlin, Germany, 3–5 June 2014; pp. 1–4. [Google Scholar]
- Bordoni, F.; Younis, M.; Cassola, M.R.; Iraol, P.P.; Dekker, P.L.; Krieger, G. SAOCOM-CS SAR imaging performance evaluation in large baseline bistatic configuration. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 2107–2110. [Google Scholar]
- Gebert, N.; Dominguez, B.C.; Martin, M.D.; Salvo, E.D.; Temussi, F.; Giove, P.V.; Gibbons, M.; Phelps, P.; Griffiths, L. SAR Instrument Pre-development Activities for SAOCOM-CS. In Proceedings of the 2016 11th European Conference on Synthetic Aperture Radar (EUSAR), Hamburg, Germany, 6–9 June 2016; pp. 1–4. [Google Scholar]
- Qiu, X.L.; Ding, C.B.; Hu, D.H. Bistatic SAR Data Processing Algorithms; John Wiley & Sons: Singapore, 2013; p. 80. ISBN 9781118188088. [Google Scholar]
- Wu, T.D.; Chen, K.S.; Shi, J.; Lee, H.W.; Fung, A.K. A study of an AIEM model for bistatic scattering from randomly rough surfaces. IEEE Trans. Geosci. Remote Sens. 2008, 46, 2584–2598. [Google Scholar] [CrossRef]
- Coello, C.A.C.; Pulido, G.T.; Lechuga, M.S. Handling multiple objectives with particle swarm optimization. IEEE Trans. Evol. Comput. 2004, 8, 256–279. [Google Scholar] [CrossRef]
- Liu, B.; Wang, L.; Jin, Y.H.; Tang, F.; Huang, D.X. Improved particle swarm optimization combined with chaos. Chaos Solitons Fractals 2005, 25, 1261–1271. [Google Scholar] [CrossRef]

















| Parameter | Symbol | Value | |
|---|---|---|---|
| System parameters | Chirp bandwidth | 45 MHz | |
| Processed Doppler bandwidth | 1050 Hz | ||
| Center frequency | 1275 MHZ | ||
| Wavelength | 23 cm | ||
| Integration time | 10 s | ||
| Transmitter peak power | 3.1 kW | ||
| Antenna gain of transmitter | 55 dB | ||
| Antenna gain of receiver | 50 dB | ||
| Receiver noise temperature | 300 K | ||
| Receiver noise figure | 4.5 dB | ||
| Propagation losses | 3.5 dB | ||
| Duty cycle | 0.05 | ||
| Motion parameters | Orbit height | 619.6 km | |
| Transmitter incidence angle | 29.55° | ||
| Transmitter azimuth angle | 0° | ||
| Flight velocity | 7545 m/s |
| Parameter | Symbol | Value |
|---|---|---|
| Population size | N | 200 |
| Particle size | m | 3 |
| Predetermined accuracy | 0.001 | |
| Maximum weight | 0.9 | |
| Minimum weight | 0.4 | |
| Maximum velocity | π/16 | |
| Acceleration coefficients 1 | 2 | |
| Acceleration coefficients 2 | 2 |
| Desired Imaging Performance | Optimal Solutions (°) | Measured Performance | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
(m) | (m) | (°) | (m2) | (dB) | (m) | (m) | (°) | (m2) | (dB) | |||
| 11.65 | 4.56 | 67.45 | 57.45 | 22.89 | 57.19 | 11.13 | 5.24 | 11.93 | 4.58 | 66.02 | 60.45 | 23.58 |
| 15.17 | 4.66 | 90.00 | 70.77 | 28.23 | 52.29 | 0.20 | 3.04 | 15.45 | 4.98 | 91.06 | 76.95 | 28.59 |
| 18.26 | 4.73 | 79.16 | 87.93 | 31.53 | 47.74 | 3.36 | 8.36 | 17.69 | 4.75 | 75.26 | 86.89 | 31.48 |
| 29.61 | 4.78 | 90.00 | 141.6 | 38.23 | 40.52 | 0.15 | 2.11 | 33.26 | 4.92 | 86.34 | 163.97 | 38.74 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, T.; Chen, K.-S.; Jin, M. Analysis and Simulation on Imaging Performance of Backward and Forward Bistatic Synthetic Aperture Radar. Remote Sens. 2018, 10, 1676. https://doi.org/10.3390/rs10111676
Li T, Chen K-S, Jin M. Analysis and Simulation on Imaging Performance of Backward and Forward Bistatic Synthetic Aperture Radar. Remote Sensing. 2018; 10(11):1676. https://doi.org/10.3390/rs10111676
Chicago/Turabian StyleLi, Tingting, Kun-Shan Chen, and Ming Jin. 2018. "Analysis and Simulation on Imaging Performance of Backward and Forward Bistatic Synthetic Aperture Radar" Remote Sensing 10, no. 11: 1676. https://doi.org/10.3390/rs10111676
APA StyleLi, T., Chen, K.-S., & Jin, M. (2018). Analysis and Simulation on Imaging Performance of Backward and Forward Bistatic Synthetic Aperture Radar. Remote Sensing, 10(11), 1676. https://doi.org/10.3390/rs10111676