Investigation on Reference Frames and Time Systems in Multi-GNSS
Abstract
:1. Introduction
- Alignment of the spatial reference frame implied by the broadcast orbits to a common frame aligned to ITRF (International Terrestrial Reference Frame), such as the one implied by the preciseephemeris of CODE (Center for Orbit Determination in Europe) at the University of Bern.
- Offset among the time scales of different GNSS constellations: are the reference time scale of the various GNSSs synchronized among each other?
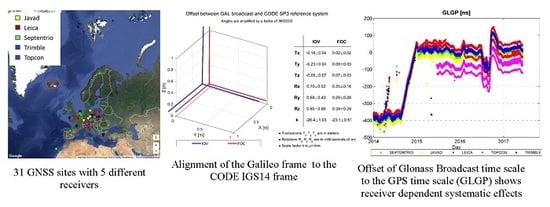
- Do different receivers measure different offsets? Does the receiver dependent offset change subject e.g., to a firmware update?
2. Quality Check of Broadcast Orbits
2.1. Comparison of Reference Systems
2.2. RSW Components of Coordinate Differences and Clock Differences
3. Data Used and Adopted Model of the Pseudorange
4. Results of the Positioning Analyses
4.1. Differential Time Offset
4.2. Analysis of Other Constellations: NAVIC and GAGAN
5. Discussion
6. Conclusions
6.1. Reference Frames
6.2. Coordinates and Clock Comparison
6.3. GNSS’s Time Offsets
Author Contributions
Conflicts of Interest
Appendix A







References
- The Multi-GNSS Experiment and Pilot Project (MGEX). Available online: http://mgex.igs.org (accessed on 29 September 2017).
- EUREF Technical Working Group (TWG). Available online: www.euref.eu/euref_twg.html (accessed on 29 September 2017).
- Montenbruck, O.; Steigenberger, P.; Hauschild, A. Broadcast versus precise ephemerides: A multi-GNSS perspective. GPS Solut. 2015, 19, 321–333. [Google Scholar] [CrossRef]
- Dalla Torre, A.; Caporali, A. An analysis of intersystem biases for multi-GNSS positioning. GPS Solut. 2015, 19, 297–307. [Google Scholar] [CrossRef]
- Caporali, A.; Nicolini, L. Interoperability of the GNSS’s for Positioning and Timing. In New Advanced GNSS and 3D Spatial Techniques; Lecture Notes in Geoinformation and Cartography; Cefalo, R., Zielinski, J., Barbarella, M., Eds.; Springer: Cham, Switzerland, 2017; pp. 73–85. ISBN 978-3-319-56218-6. [Google Scholar]
- Prange, L.; Orliac, E.; Dach, R.; Arnold, D.; Beutler, G.; Schaer, S.; Jäggi, A. CODE’s five-system orbit and clock solution—The challenges of multi-GNSS data analysis. J. Geod. 2017, 91, 345–360. [Google Scholar] [CrossRef]
- Revnivykh, S. GLONASS ground control segment: Orbit, clock, time scale and geodesy definition. In Proceedings of the 25th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2012), Nashville, TN, USA, 17–21 September 2012; pp. 3931–3949. [Google Scholar]
- Kosenko, V. Global Navigation Satellite System (GLONASS): Status and Development. In United Nations/Russian Federation Workshop on the Applications of Global Navigation Satellite Systems; Russian Federation: Krasnoyarsk, Russia, 2015. [Google Scholar]
- Teunissen, P.J.G.; Montenbruck, O. Springer Handbook of Global Navigation Satellite Systems, 1st ed.; Springer International Publishing: Cham, Switzerland, 2017; ISBN 978-3-319-42926-7. [Google Scholar]
- Dach, R.; Lutz, S.; Walser, P.; Fridez, P. Bernese GNSS Software Version 5.2. User Manual; University of Bern, Bern Open Publishing: Bern, Switzerland, 2015; ISBN 978-3-906813-05-9. [Google Scholar]
- EU. European GNSS (Galileo) Open Service Signal in Space Interface Control Document. Available online: https://www.gsc-europa.eu/system/files/galileo_documents/Galileo-OS-SIS-ICD.pdf (accessed on 4 January 2018).
- Steigenberger, P.; Montenbruck, O. Galileo status: Orbits, clocks, and positioning. GPS Solut. 2017, 21, 319–331. [Google Scholar] [CrossRef]
- International GNSS Service (IGS) RINEX Working Group and Radio Technical Commission for Maritime Services Special Committee 104 (RTCM-SC104). RINEX The Receiver Independent Exchange Format; Version 3.03; Werner Gurtner, Astronomical Institute of the University of Bern, Switzerland and Lou Estey, UNAVCO: Boulder, CO, USA, 2015. [Google Scholar]
- Nischan, T. GFZRNX–RINEX GNSS Data Conversion and Manipulation Toolbox (Version 1.05). Available online: http://dataservices.gfz-potsdam.de/panmetaworks/showshort.php?id=escidoc:1577894 (accessed on 4 January 2018).
- Russian Institute of Space Device Engineering (RISDE). Global Navigation Satellite System GLONASS—Interface Control Document; Version 5.1; Russian Institute of Space Device Engineering: Moscow, Russia, 2008. [Google Scholar]
- Håkansson, M.; Jensen, A.B.O.; Horemuz, M.; Hedling, G. Review of code and phase biases in multi-GNSS positioning. GPS Solut. 2017, 21, 849–860. [Google Scholar] [CrossRef]
- Zeng, A.; Yang, Y.; Ming, F.; Jing, Y. BDS-GPS inter-system bias of code observation and its preliminary analysis. GPS Solut. 2017, 21, 1417–1425. [Google Scholar] [CrossRef]
- Jiang, N.; Xu, Y.; Xu, T.; Xu, G.; Sun, Z.; Schuh, H. GPS/BDS short-term ISB modelling and prediction. GPS Solut. 2017, 21, 163–175. [Google Scholar] [CrossRef]
- Odijk, D.; Teunissen, P.J.G. Characterization of between-receiver GPS-Galileo inter-system biases and their effect on mixed ambiguity resolution. GPS Solut. 2013, 17, 521–533. [Google Scholar] [CrossRef]
- Gioia, C.; Borio, D. A statistical characterization of the Galileo-to-GPS inter-system bias. J. Geod. 2016, 90, 1279–1291. [Google Scholar] [CrossRef]
- Chen, J.; Xiao, P.; Zhang, Y.; Wu, B. GPS/GLONASS System Bias Estimation and Application in GPS/GLONASS Combined Positioning. In China Satellite Navigation Conference (CSNC) 2013 Proceedings. Lecture Notes in Electrical Engineering; Sun, J., Jiao, W., Wu, H., Shi, C., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 323–333. ISBN 978-3-642-37403-6. [Google Scholar]













| ID | City | Country | Domes | Receiver | Antenna | Start Date |
|---|---|---|---|---|---|---|
| BBYS | Banka Bystrica | Slovak Republic | 11514M001 | Trimble NETR9 | TRM59800.00 | 1 January 2014 |
| BOGO | Borowa Gora | Poland | 12207M002 | Topcon EUROCARD | ASH700936C_M | 21 June 2015 |
| BRST | Brest | France | 10004M004 | Trimble NETR9 | TRM57971.00 | 1 January 2014 |
| BRUX | Brussels | Belgium | 13101M010 | Septentrio POLARX4TR | JAVRINGANT_DM | 1 January 2014 |
| CAEN | Caen | France | 19994M001 | Leica GR25 | TRM57971.00 | 1 January 2014 |
| CEBR | Cebreros | Spain | 13408M001 | Septentrio POLARX4 | SEPCHOKE_MC | 1 January 2014 |
| COMO | Como | Italy | 12761M001 | Topcon E_GGD | TPSCR3_GGD | 21 June 2015 |
| COMO | Como | Italy | 12761M001 | Topcon NET-G5 | TPSCR3_GGD | 19 October 2016 |
| COMO | Como | Italy | 12761M001 | Topcon NET-G5 | TPSCR.G3 | 7 February 2017 |
| DLF1 | Delft | The Netherlands | 13502M009 | Trimble NETR9 | LEIAR25.R3 | 1 January 2014 |
| DYNG | Dyonisos | Greece | 12602M006 | Trimble NETR9 | TRM59800.00 | 2 March 2015 |
| GANP | Ganovce | Slovak Republic | 11515M001 | Trimble NETR9 | TRM55971.00 | 1 January 2014 |
| GANP | Ganovce | Slovak Republic | 11515M001 | Trimble NETR9 | TRM59800.00 | 6 February 2017 |
| GOP7 | Ondrejov | Slovak Republic | 11502M006 | Javad TRE_G3TH DELTA | LEIAR25.R4 | 1 January 2014 |
| GOP7 | Ondrejov | Slovak Republic | 11502M006 | Trimble NETR9 | LEIAR25.R4 | 1 January 2014 |
| HOFN | Hoefn | Iceland | 10204M002 | Leica GR25 | LEIAR25.R4 | 1 January 2014 |
| IGMI | Firenze | Italy | 12701M003 | Topcon ODYSSEY_E | TPSCR.G3 | 21 June 2015 |
| KIRU | Kiruna | Sweden | 10403M002 | Septentrio POLARX4 | SEPCHOKE_MC | 1 January 2014 |
| M0SE | Roma | Italy | 12772M001 | Leica GR25 | LEIAR25.R4 | 1 January 2014 |
| MAS1 | Maspalomas | Spain | 31303M002 | Septentrio POLARX4 | LEIAR25.R4 | 25 October 2015 |
| MLVL | Marne-la-Vallee | France | 10092M001 | Leica GR25 | TRM57971.00 | 1 January 2014 |
| NYA2 | Ny Alesund | Norway | 10317M008 | Javad TRE_G3TH DELTA | JAV_RINGANT_G3T | 25 October 2015 |
| OBE4 | Oberpfaffenhofen | Germany | 14208M007 | Javad TRE_G3TH DELTA | JAV_RINGANT_G3T | 25 October 2015 |
| PADO | Padova | Italy | 12750S001 | Leica GR10 | LEIAR25.R4 | 1 January 2014 |
| PEN2 | Penc | Hungary | 11206M007 | Leica GRX1200 + GNSS | LEIAR25.R4 | 2 March 2015 |
| POTS | Potsdam | Germany | 14106M003 | Javad TRE_G3TH DELTA | JAV_RINGANT_G3T | 2 March 2015 |
| REDU | Redu | Belgium | 13102M001 | Septentrio POLARX4 | SEPCHOKE_MC | 2 March 2015 |
| REYK | Reykjavik | Iceland | 10202M001 | Leica GR25 | LEIAR25.R4 | 2 March 2015 |
| SULP | Lviv | Ukraine | 12366M001 | Topcon NET-G3A | TPSCR.G5 | 21 June 2015 |
| TLSE | Toulouse | France | 10003M009 | Trimble NETR9 | TRM59800.00 | 2 March 2015 |
| VILL | Villafranca | Spain | 13406M001 | Septentrio POLARX4 | SEPCHOKE_MC | 25 October 2015 |
| WROC | Wroclaw | Poland | 12217M001 | Leica GR25 | LEIAR25.R4 | 2 March 2015 |
| WTZ3 | Bad Koetzting | Germany | 14201M015 | Javad TRE_G3TH DELTA | LEIAR25.R3 | 25 October 2015 |
| WTZZ | Bad Koetzting | Germany | 14201M014 | Javad TRE_G3TH DELTA | LEIAR25.R3 | 1 January 2014 |
| ZIMJ | Zimmerwald | Switzerland | 14001M006 | Javad TRE_G3TH DELTA | JAVRINGANT_DM | 1 January 2014 |
| Satellite | Radial (m) | Along-Track (m) | Cross-Track (m) | Clock (ns) | Block | Clock 1 |
|---|---|---|---|---|---|---|
| G01 | 0.00 ± 0.12 | −0.09 ± 0.44 | 0.30 ± 0.27 | −0.9 ± 0.8 | IIF | Rb |
| G02 | 0.05 ± 0.13 | −0.17 ± 0.74 | 0.08 ± 0.50 | 1.6 ± 0.8 | IIR-B | Rb |
| G03 | 0.00 ± 0.15 | −0.08 ± 0.62 | 0.27 ± 0.35 | −2.4 ± 0.8 | IIF | Rb |
| G05 | 0.00 ± 0.10 | 0.02 ± 0.66 | 0.19 ± 0.25 | 1.8 ± 0.6 | IIR-M | Rb |
| G06 | 0.01 ± 0.15 | −0.06 ± 0.79 | 0.28 ± 0.34 | −0.3 ± 0.5 | IIF | Rb |
| G07 | −0.02 ± 0.11 | −0.03 ± 0.62 | 0.00 ± 0.38 | 0.5 ± 1.7 | IIR-M | Rb |
| G08 | −0.02 ± 0.29 | 0.00 ± 0.95 | −0.03 ± 0.29 | −0.2 ± 3.6 | IIF | Cs |
| G09 | 0.01 ± 0.27 | 0.04 ± 0.42 | 0.30 ± 0.27 | 0.0 ± 0.8 | IIF | Rb |
| G10 | −0.05 ± 0.12 | 0.25 ± 0.67 | 0.28 ± 0.36 | −1.0 ± 0.6 | IIF | Rb |
| G11 | 0.04 ± 0.14 | 0.36 ± 0.43 | 0.00 ± 0.24 | −3.1 ± 1.3 | IIR-A | Rb |
| G12 | 0.03 ± 0.10 | 0.32 ± 0.93 | −0.07 ± 0.28 | 0.7 ± 0.8 | IIR-M | Rb |
| G13 | −0.02 ± 0.13 | −0.11 ± 0.57 | 0.04 ± 0.47 | −3.4 ± 0.8 | IIR-A | Rb |
| G14 | −0.04 ± 0.13 | 0.80 ± 0.63 | 0.04 ± 0.52 | −2.3 ± 0.5 | IIR-A | Rb |
| G15 | −0.07 ± 0.08 | 0.72 ± 1.06 | 0.11 ± 0.19 | 0.7 ± 0.7 | IIR-M | Rb |
| G16 | −0.08 ± 0.08 | −0.18 ± 0.50 | −0.04 ± 0.42 | −1.8 ± 0.6 | IIR-A | Rb |
| G17 | 0.03 ± 0.16 | 0.74 ± 1.12 | −0.05 ± 0.31 | 0.4 ± 2.0 | IIR-M | Rb |
| G18 | 0.05 ± 0.10 | −0.66 ± 0.88 | 0.14 ± 0.32 | −2.1 ± 1.3 | IIR-A | Rb |
| G19 | −0.02 ± 0.13 | 0.50 ± 0.77 | −0.06 ± 0.54 | 1.3 ± 1.0 | IIR-B | Rb |
| G20 | 0.00 ± 0.09 | −0.46 ± 0.77 | 0.13 ± 0.27 | −2.0 ± 0.9 | IIR-A | Rb |
| G21 | −0.02 ± 0.12 | 0.02 ± 0.82 | 0.03 ± 0.38 | −1.8 ± 0.8 | IIR-A | Rb |
| G22 | −0.11 ± 0.10 | 0.30 ± 0.46 | 0.20 ± 0.46 | 1.8 ± 0.8 | IIR-B | Rb |
| G23 | 0.01 ± 0.08 | −0.57 ± 0.68 | 0.13 ± 0.44 | 0.5 ± 0.6 | IIR-B | Rb |
| G24 | −0.01 ± 0.42 | 0.56 ± 1.11 | −0.07 ± 0.31 | −2.6 ± 2.6 | IIF | Cs |
| G25 | 0.00 ± 0.17 | 0.22 ± 0.62 | −0.17 ± 0.37 | −1.3 ± 0.8 | IIF | Rb |
| G26 | 0.03 ± 0.21 | −0.47 ± 0.64 | −0.13 ± 0.26 | −0.5 ± 0.5 | IIF | Rb |
| G27 | −0.02 ± 0.30 | 0.08 ± 0.68 | −0.02 ± 0.24 | −0.9 ± 0.7 | IIF | Rb |
| G28 | 0.08 ± 0.13 | −0.12 ± 0.61 | −0.02 ± 0.18 | −2.6 ± 3.9 | IIR-A | Rb |
| G29 | 0.06 ± 0.12 | −0.92 ± 0.74 | −0.07 ± 0.45 | 2.0 ± 1.0 | IIR-M | Rb |
| G30 | 0.03 ± 0.22 | −0.23 ± 0.53 | −0.09 ± 0.25 | −0.8 ± 0.8 | IIF | Rb |
| G31 | 0.04 ± 0.13 | −0.25 ± 0.81 | 0.00 ± 0.29 | 0.8 ± 0.8 | IIR-M | Rb |
| G32 | 0.01 ± 0.19 | −0.21 ± 0.70 | 0.29 ± 0.31 | −0.6 ± 0.6 | IIF | Rb |
| Satellite | Radial (m) | Along-Track (m) | Cross-Track (m) | Clock (ns) | Block | Clock 1 |
|---|---|---|---|---|---|---|
| R01 | 0.10 ± 0.41 | −0.42 ± 0.70 | −0.19 ± 0.62 | −2.4 ± 3.0 | M | Cs |
| R02 | 0.07 ± 0.44 | −0.03 ± 1.13 | −0.14 ± 0.67 | −6.1 ± 5.8 | M | Cs |
| R03 | 0.08 ± 0.40 | 0.78 ± 0.87 | −0.12 ± 0.97 | 20.1 ± 6.0 | M | Cs |
| R04 | 0.08 ± 0.41 | −0.72 ± 1.10 | −0.16 ± 0.45 | 22.2 ± 6.3 | M | Cs |
| R05 | 0.08 ± 0.39 | 1.22 ± 1.58 | −0.18 ± 0.90 | −1.5 ± 5.8 | M | Cs |
| R06 | 0.16 ± 0.47 | 0.79 ± 1.72 | −0.17 ± 0.54 | 0.1 ± 5.9 | M | Cs |
| R07 | 0.14 ± 0.38 | 0.46 ± 1.01 | −0.12 ± 0.62 | 14.6 ± 4.3 | M | Cs |
| R08 | 0.12 ± 0.41 | −0.41 ± 1.15 | −0.15 ± 0.97 | 24.3 ± 4.4 | M | Cs |
| R09 | 0.00 ± 0.58 | 0.00 ± 0.79 | 0.00 ± 0.36 | 10.3 ± 3.9 | K | Cs |
| R10 | −0.29 ± 0.49 | −0.21 ± 0.73 | 0.18 ± 1.06 | −13.9 ± 7.2 | M | Cs |
| R11 | 0.05 ± 0.42 | 1.91 ± 0.89 | 0.18 ± 0.65 | 6.4 ± 5.3 | M | Cs |
| R13 | 0.08 ± 0.46 | −0.31 ± 2.35 | 0.15 ± 0.73 | −3.1 ± 4.7 | M | Cs |
| R14 | −0.30 ± 0.46 | −0.23 ± 2.94 | 0.14 ± 0.93 | −20.2 ± 9.7 | M | Cs |
| R15 | −0.30 ± 0.49 | −1.13 ± 2.32 | 0.09 ± 0.99 | 0.6 ± 9.9 | M | Cs |
| R16 | −0.01 ± 0.44 | 1.31 ± 1.12 | 0.09 ± 0.69 | 3.7 ± 5.2 | M | Cs |
| R17 | 0.03 ± 0.62 | 2.31 ± 0.88 | −0.13 ± 0.74 | 11.8 ± 5.0 | M | Cs |
| R18 | −0.01 ± 0.48 | 0.31 ± 0.87 | −0.15 ± 0.76 | −4.6 ± 4.3 | M | Cs |
| R19 | 0.06 ± 0.66 | 1.06 ± 2.00 | −0.09 ± 0.78 | 6.9 ± 5.9 | M | Cs |
| R20 | −0.35 ± 0.64 | 0.01 ± 2.19 | −0.11 ± 0.71 | 5.1 ± 4.8 | M | Cs |
| R21 | 0.02 ± 0.53 | 0.35 ± 0.82 | −0.08 ± 0.66 | 13.1 ± 4.7 | M | Cs |
| R22 | 0.03 ± 0.46 | −1.17 ± 1.87 | −0.07 ± 0.72 | 0.0 ± 7.5 | M | Cs |
| R23 | −0.05 ± 0.52 | 1.78 ± 0.97 | −0.08 ± 0.67 | 2.2 ± 4.7 | M | Cs |
| R24 | 0.18 ± 0.57 | −0.96 ± 1.02 | −0.09 ± 0.79 | 6.2 ± 3.5 | M | Cs |
| Satellite | Radial (m) | Along-Track (m) | Cross-Track (m) | Clock (ns) | Orbit | Clock 3 |
|---|---|---|---|---|---|---|
| C06 | −1.15 ± 0.31 | 0.14 ± 0.51 | −0.01 ± 0.59 | 104.8 ± 2.2 | IGSO 1 | Rb |
| C07 | 0.99 ± 0.35 | −0.03 ± 0.60 | −0.21 ± 0.44 | 121.5 ± 2.0 | IGSO 1 | Rb |
| C08 | 0.31 ± 0.48 | 0.51 ± 0.39 | 0.09 ± 0.86 | 113.6 ± 2.4 | IGSO 1 | Rb |
| C09 | −0.28 ± 0.30 | −0.32 ± 0.43 | −0.13 ± 0.77 | 94.8 ± 2.0 | IGSO 1 | Rb |
| C10 | −0.14 ± 0.32 | 0.39 ± 0.70 | −0.07 ± 0.46 | 95.5 ± 2.3 | IGSO 1 | Rb |
| C11 | −0.39 ± 0.55 | −0.20 ± 1.26 | 0.04 ± 0.64 | 88.4 ± 27.2 | MEO 2 | Rb |
| C12 | −0.03 ± 0.49 | 0.02 ± 1.33 | 0.02 ± 0.54 | 93.1 ± 2.5 | MEO 2 | Rb |
| C13 | 0.26 ± 0.63 | −0.22 ± 0.61 | −0.03 ± 0.81 | 55.8 ± 1.6 | IGSO 1 | Rb |
| C14 | 0.43 ± 0.45 | −0.53 ± 1.48 | 0.50 ± 0.59 | 99.9 ± 3.1 | MEO 2 | Rb |
| Satellite | Radial (m) | Along-Track (m) | Cross-Track (m) | Clock (ns) | Generation | Clock 3 |
|---|---|---|---|---|---|---|
| E01 | 0.01 ± 0.14 | −0.13 ± 0.28 | −0.04 ± 0.16 | 2.2 ± 1.3 | FOC 2 | PHM |
| E02 | −0.01 ± 0.15 | −0.06 ± 0.29 | 0.04 ± 0.13 | 1.3 ± 1.1 | FOC 2 | PHM |
| E03 | 0.01 ± 0.11 | −0.10 ± 0.25 | 0.00 ± 0.17 | 2.1 ± 1.2 | FOC 2 | PHM |
| E04 | −0.01 ± 0.11 | −0.05 ± 0.36 | 0.01 ± 0.16 | 1.6 ± 1.2 | FOC 2 | PHM |
| E05 | −0.03 ± 0.12 | 0.00 ± 0.25 | 0.01 ± 0.16 | 2.1 ± 1.1 | FOC 2 | PHM |
| E07 | 0.01 ± 0.12 | −0.11 ± 0.28 | 0.05 ± 0.16 | 2.8 ± 1.3 | FOC 2 | PHM |
| E08 | −0.01 ± 0.11 | 0.04 ± 0.24 | 0.04 ± 0.14 | 1.0 ± 1.2 | FOC 2 | PHM |
| E09 | 0.00 ± 0.13 | 0.05 ± 0.30 | 0.03 ± 0.17 | 1.7 ± 1.2 | FOC 2 | PHM |
| E11 | 0.01 ± 0.15 | 0.00 ± 0.35 | −0.05 ± 0.18 | 0.7 ± 1.2 | IOV 1 | PHM |
| E12 | 0.00 ± 0.13 | −0.04 ± 0.31 | −0.04 ± 0.17 | 1.6 ± 1.4 | IOV 1 | PHM |
| E14 | 0.04 ± 0.48 | 0.04 ± 2.10 | −0.14 ± 0.84 | 6.7 ± 1.3 | FOC 2 | PHM |
| E18 | 0.04 ± 0.37 | −0.04 ± 2.05 | −0.02 ± 0.50 | 4.1 ± 1.2 | FOC 2 | PHM |
| E19 | −0.01 ± 0.18 | −0.08 ± 0.44 | −0.01 ± 0.23 | 1.1 ± 1.5 | IOV 1 | PHM |
| E22 | −0.01 ± 0.16 | 0.03 ± 0.25 | −0.05 ± 0.13 | 1.4 ± 1.5 | FOC 2 | PHM |
| E24 | −0.02 ± 0.15 | 0.01 ± 0.25 | −0.05 ± 0.17 | 7.8 ± 1.1 | FOC 2 | PHM |
| E26 | 0.01 ± 0.16 | −0.09 ± 0.29 | −0.06 ± 0.15 | 2.5 ± 1.3 | FOC 2 | PHM |
| E30 | 0.02 ± 0.15 | −0.02 ± 0.22 | 0.02 ± 0.16 | 2.0 ± 1.2 | FOC 2 | PHM |
| Constellation | Carrier/Frequency [MHz] | Pseudorange Codes | ||
|---|---|---|---|---|
| GPS | L1 (1575.42) | L2 (1227.60) | C1C | C2W |
| GLONASS | G1 (1602 + k × 9/16) | G2 (1246 + k × 7/16) | C1C | C2P |
| Galileo | E1 (1575.42) | E5b 1 (1207.14) | C1C | C7I/C7Q/C7X |
| BeiDou | B1 (1561.098) | B2 (1207.14) | C1I | C7I |
| QZSS | L1 (1575.42) | L2 (1227.60) | C1C | C2S/C2L/C2X |
| NAVIC | L5 (1176.45) | C5A | ||
| SBAS | L1 (1575.42) | L5 (1176.45) | C1C | C5I |
| Symbol | Unit | Meaning |
|---|---|---|
| c | m/s | Speed of light |
| t | s | Time of reception in the receiver time scale |
| t‘ | s | Time of transmission in the specific GNSS time scale: t′ = t − p(t)/c |
| tof | s | Time of flight |
| LS | s | Position of satellites must be computed at time t − tof − LS, where LS = full leap seconds for GLONASS; 14 s for BeiDou; 0 s for other GNSS |
| dTRel | s | Periodic part of relativistic correction (which is not considered for GLONASS since it is already included in the polynomial correction [3]) |
| ωe | rad/s | Earth rotation rate appropriate for the GNSS constellation |
| X, Y, Z | m | Earth-Centered Earth-Fixed (ECEF) coordinates of satellite |
| x, y, z | m | ECEF coordinates of receiver |
| TSCX | s | Time System Correction of the X 1 GNSS relative to a common time scale |
| dTRec | s | Receiver clock offset relative to a common time scale |
| dt | s | Satellite Clock offset relative to a specific GNSS time scale |
| TZD | m | Tropospheric Zenith Delay |
| El | ° | Elevation |
| Time Offset | Definition |
|---|---|
| GLGP | (TSCR + dTRec) − (TSCG + dTRec) |
| GPGA | (TSCG + dTRec) − (TSCE + dTRec) |
| BDGP | (TSCC + dTRec) − (TSCG + dTRec) |
| QZGP | (TSCJ + dTRec) − (TSCG + dTRec) |
| NAGP | (TSCI + dTRec) − (TSCG + dTRec) |
| GNGP | (TSCN + dTRec) − (TSCG + dTRec) |
| STATION | RECEIVER | CALIBRATION [ns] | |||||||
|---|---|---|---|---|---|---|---|---|---|
| ID | FROM | TO | RECEIVER | TYPE | FIRMWARE | dGLGP | dGPGA | dBDGP | dQZGP |
| BBYSa | 1 January 2014 | 30 May 2014 | TRIMBLE | NETR9 | 4.81/4.71 | 16.5 ± 2.7 | 44.4 ± 2.8 | ||
| BBYSb | 30 May 2014 | NOW 1 | TRIMBLE | NETR9 | 4.85/4.71 | 10.6 ± 0.9 | −12.4 ± 0.8 | 40.1 ± 1.7 | |
| BOGO | 21 June 2015 | NOW 1 | TOPCON | EUROCARD | 2.6.1 10 January 2008 | −118.1 ± 1.1 | |||
| BRST | 1 January 2014 | 26 March 2014 | TRIMBLE | NETR9 | 4.81 | 11.1 ± 1.2 | −12.0 ± 1.1 | 38.9 ± 2.4 | |
| BRST | 26 March 2014 | NOW 1 | TRIMBLE | NETR9 | 4.85 | 11.1 ± 1.2 | −12.0 ± 1.1 | 38.9 ± 2.4 | |
| BRUX | 1 January 2014 | 17 March 2014 | SEPTENTRIO | POLARX4TR | 2.3.4 | 2.8 ± 2.7 | 0.6 ± 0.6 | 3.4 ± 3.3 | |
| BRUX | 17 March 2014 | 7 September 2015 | SEPTENTRIO | POLARX4TR | 2.5.2 | 2.8 ± 2.7 | 0.6 ± 0.6 | 3.4 ± 3.3 | |
| BRUX | 7 September 2015 | 24 October 2016 | SEPTENTRIO | POLARX4TR | 2.9.0 | 2.8 ± 2.7 | 0.6 ± 0.6 | 3.4 ± 3.3 | |
| BRUX | 24 October 2016 | 3 January 2017 | SEPTENTRIO | POLARX4TR | 2.9.5 | 2.8 ± 2.7 | 0.6 ± 0.6 | 3.4 ± 3.3 | |
| BRUX | 3 January 2017 | NOW 1 | SEPTENTRIO | POLARX4TR | 2.9.6 | 2.8 ± 2.7 | 0.6 ± 0.6 | 3.4 ± 3.3 | |
| CAENa | 1 January 2014 | 20 February 2014 | LEICA | GR25 | 3.01 | 41.5 ± 3.2 | −42.1 ± 1.1 | 68.0 ± 3.3 | |
| CAENa | 20 February 2014 | 19 September 2014 | LEICA | GR25 | 3.03 | 41.5 ± 3.2 | −42.1 ± 1.1 | 68.0 ± 3.3 | |
| CAENa | 19 September 2014 | 6 November 2014 | LEICA | GR25 | 3.10 | 41.5 ± 3.2 | −42.1 ± 1.1 | 68.0 ± 3.3 | |
| CAENa | 6 November 2014 | 5 August 2016 | LEICA | GR25 | 3.11 | 41.5 ± 3.2 | −42.1 ± 1.1 | 68.0 ± 3.3 | |
| CAENb | 12 August 2016 | 9 November 2016 | LEICA | GR25 | 3.11 | −23.9 ± 0.5 | −65.3 ± 1.0 | 90.3 ± 2.7 | |
| CAENb | 9 November 2016 | NOW 1 | LEICA | GR25 | 4.02 | −23.9 ± 0.5 | −65.3 ± 1.0 | 90.3 ± 2.7 | |
| CEBR | 1 January 2014 | 10 December 2014 | SEPTENTRIO | POLARX4 | 2.5.1p1 | −0.3 ± 2.8 | 0.0 ± 0.9 | −2.9 ± 3.2 | |
| CEBR | 10 December 2014 | 27 August 2015 | SEPTENTRIO | POLARX4 | 2.5.2-esa3 | −0.3 ± 2.8 | 0.0 ± 0.9 | −2.9 ± 3.2 | |
| CEBR | 27 August 2015 | 21 October 2016 | SEPTENTRIO | POLARX4 | 2.9.0 | −0.3 ± 2.8 | 0.0 ± 0.9 | −2.9 ± 3.2 | |
| CEBR | 21 October 2016 | NOW 1 | SEPTENTRIO | POLARX4 | 2.9.5-extref1 | −0.3 ± 2.8 | 0.0 ± 0.9 | −2.9 ± 3.2 | |
| COMOa | 21 June 2015 | 19 October 2016 | TOPCON | E_GGD | 3.4 12 Decembaer 2009 p2 | −76.2 ± 2.0 | |||
| COMOb | 19 October 2016 | 7 February 2017 | TOPCON | NET-G5 | 5.0 20 November 2015 p2 | −60.2 ± 0.7 | |||
| COMOc | 7 February 2017 | NOW 1 | TOPCON | NET-G5 | 5.1 7 September 2016 | −56.0 ± 0.8 | |||
| DLF1a | 1 January 2014 | 17 June 2015 | TRIMBLE | NETR9 | 4.81 | 23.6 ± 1.8 | 44.8 ± 1.4 | ||
| DLF1b | 17 June 2015 | 13 July 2015 | TRIMBLE | NETR9 | 5.01 | 17.4 ± 0.9 | −16.2 ± 1.0 | 42.2 ± 1.4 | −102.9 ± 149.4 |
| DLF1b | 13 July 2015 | 20 July 2016 | TRIMBLE | NETR9 | 5.03 | 17.4 ± 0.9 | −16.2 ± 1.0 | 42.2 ± 1.4 | −102.9 ± 149.4 |
| DLF1b | 20 July 2016 | 21 December 2016 | TRIMBLE | NETR9 | 5.14 | 17.4 ± 0.9 | −16.2 ± 1.0 | 42.2 ± 1.4 | −102.9 ± 149.4 |
| DLF1b | 21 December 2016 | 28 May 2017 | TRIMBLE | NETR9 | 5.15 | 17.4 ± 0.9 | −16.2 ± 1.0 | 42.2 ± 1.4 | −102.9 ± 149.4 |
| DLF1b | 28 May 2017 | NOW 1 | TRIMBLE | NETR9 | 5.22 | 17.4 ± 0.9 | −16.2 ± 1.0 | 42.2 ± 1.4 | −102.9 ± 149.4 |
| DYNGa | 2 March 2015 | 19 June 2015 | TRIMBLE | NETR9 | 4.85 | 12.3 ± 1.4 | −13.0 ± 1.3 | 38.0 ± 2.1 | |
| DYNGa | 19 June 2015 | 5 July 2016 | TRIMBLE | NETR9 | 5.01 | 12.3 ± 1.4 | −13.0 ± 1.3 | 38.0 ± 2.1 | |
| DYNGb | 05 July 2016 | 14 December 2016 | TRIMBLE | NETR9 | 5.14 | 15.4 ± 1.7 | −13.6 ± 1.1 | 44.1 ± 1.4 | |
| DYNGb | 14 December 2016 | NOW 1 | TRIMBLE | NETR9 | 5.15 | 15.4 ± 1.7 | −13.6 ± 1.1 | 44.1 ± 1.4 | |
| GANPa | 1 January 2014 | 30 May 2014 | TRIMBLE | NETR9 | 4.81/4.29 | 13.0 ± 2.6 | 40.5 ± 1.5 | ||
| GANPb | 30 May 2014 | 10 February 2015 | TRIMBLE | NETR9 | 4.85/4.29 | 10.3 ± 3.6 | −14.7 ± 2.1 | 38.5 ± 3.4 | −21.8 ± 53.1 |
| GANPb | 10 February 2015 | 18 November 2015 | TRIMBLE | NETR9 | 4.93/4.93 | 10.3 ± 3.6 | −14.7 ± 2.1 | 38.5 ± 3.4 | −21.8 ± 53.1 |
| GANPb | 18 November 2015 | 14 October 2016 | TRIMBLE | NETR9 | 5.10/5.02 | 10.3 ± 3.6 | −14.7 ± 2.1 | 38.5 ± 3.4 | −21.8 ± 53.1 |
| GANPb | 14 October 2016 | 2 January 2017 | TRIMBLE | NETR9 | 5.14/5.14 | 10.3 ± 3.6 | −14.7 ± 2.1 | 38.5 ± 3.4 | −21.8 ± 53.1 |
| GANPb | 2 January 2017 | 11 January 2017 | TRIMBLE | NETR9 | 5.15/5.15 | 10.3 ± 3.6 | −14.7 ± 2.1 | 38.5 ± 3.4 | −21.8 ± 53.1 |
| GANPb | 11 January 2017 | 6 February 2017 | TRIMBLE | NETR9 | 5.20/5.20 | 10.3 ± 3.6 | −14.7 ± 2.1 | 38.5 ± 3.4 | −21.8 ± 53.1 |
| GANPc | 6 February 2017 | 18 April 2017 | TRIMBLE | NETR9 | 5.20 | 17.4 ± 0.9 | −11.0 ± 0.9 | 44.9 ± 0.8 | −30.4± 30.6 |
| GANPc | 18 April 2017 | NOW 1 | TRIMBLE | NETR9 | 5.22 | 17.4 ± 0.9 | −11.0 ± 0.9 | 44.9 ± 0.8 | −30.4 ± 30.6 |
| GOP7a | 1 January 2014 | 21 August 2015 | JAVAD | TRE_G3TH DELTA | 3.5.1 | −19.0 ± 1.3 | |||
| GOP7b | 21 August 2015 | NOW 1 | TRIMBLE | NETR9 | 5.01 | 10.6 ± 3.0 | −4.9 ± 4.6 | 35.1 ± 3.1 | |
| HOFN | 1 January 2014 | 18 February 2014 | LEICA | GR25 | 3.01/6.212 | 43.8 ± 3.5 | −44.2 ± 0.8 | ||
| HOFN | 18 February 2014 | 8 September 2014 | LEICA | GR25 | 3.03/6.214 | 43.8 ± 3.5 | −44.2 ± 0.8 | ||
| HOFN | 8 September 2014 | 10 September 2014 | LEICA | GR25 | 3.10/6.403 | 43.8 ± 3.5 | −44.2 ± 0.8 | ||
| HOFN | 10 September 2014 | 3 November 2014 | LEICA | GR25 | 3.10.1633/6.403 | 43.8 ± 3.5 | −44.2 ± 0.8 | ||
| HOFN | 3 November 2014 | NOW 1 | LEICA | GR25 | 3.11.1639/6.403 | 43.8 ± 3.5 | −44.2 ± 0.8 | ||
| IGMI | 21 June 2015 | 17 June 2016 | TOPCON | ODYSSEY_E | 3.3 10 July 2008 P4 | −69.3 ± 1.5 | |||
| IGMI | 21 July 2016 | NOW 1 | TOPCON | ODYSSEY_E | 3.4 12 December 2009 P2 | −69.3 ± 1.5 | |||
| KIRU | 1 January 2014 | 10 December 2014 | SEPTENTRIO | POLARX4 | 2.5.1p1 | −3.4 ± 2.1 | −0.4 ± 1.2 | 2.1 ± 3.8 | 0.0 ± 0.0 |
| KIRU | 10 December 2014 | 27 August 2015 | SEPTENTRIO | POLARX4 | 2.5.2-esa3 | −3.4 ± 2.1 | −0.4 ± 1.2 | 2.1 ± 3.8 | 0.0 ± 0.0 |
| KIRU | 27 August 2015 | 21 October 2016 | SEPTENTRIO | POLARX4 | 2.9.0 | −3.4 ± 2.1 | −0.4 ± 1.2 | 2.1 ± 3.8 | 0.0 ± 0.0 |
| KIRU | 21 October 2016 | NOW 1 | SEPTENTRIO | POLARX4 | 2.9.5-extref1 | −3.4 ± 2.1 | −0.4 ± 1.2 | 2.1 ± 3.8 | 0.0 ± 0.0 |
| M0SEa | 1 January 2014 | 24 February 2014 | LEICA | GR25 | 3.00/6.113 | 41.1 ± 4.1 | |||
| M0SEa | 24 February 2014 | 17 July 2014 | LEICA | GR25 | 3.03/6.214 | 41.1 ± 4.1 | |||
| M0SEa | 17 July 2014 | 11 September 2014 | LEICA | GR25 | 3.10/6.401 | 41.1 ± 4.1 | |||
| M0SEa | 11 September 2014 | 26 November 2014 | LEICA | GR25 | 3.10/6.403 | 41.1 ± 4.1 | |||
| M0SEa | 26 November 2014 | 8 May 2015 | LEICA | GR25 | 3.11/6.403 | 41.1 ± 4.1 | |||
| M0SEa | 8 May 2015 | 2 February 2016 | LEICA | GR25 | 3.20/6.403 | 41.1 ± 4.1 | |||
| M0SEb | 2 February 2016 | 03 April 2017 | LEICA | GR25 | 3.22/6.521 | −24.9 ± 0.6 | −67.4 ± 0.8 | ||
| M0SEb | 3 April 2017 | NOW 1 | LEICA | GR25 | 4.11/6.523 | −24.9 ± 0.6 | −67.4 ± 0.8 | ||
| MAS1 | 25 October 2015 | 18 October 2016 | SEPTENTRIO | POLARX4 | 2.9.0 | −1.2 ± 0.8 | 0.2 ± 1.2 | −4.3 ± 2.3 | |
| MAS1 | 18 October 2016 | NOW 1 | SEPTENTRIO | POLARX4 | 2.9.5-extref1 | −1.2 ± 0.8 | 0.2 ± 1.2 | −4.3 ± 2.3 | |
| MLVLa | 1 January 2014 | 29 January 2014 | LEICA | GR25 | 3.01 | 37.3 ± 2.8 | −39.8 ± 1.2 | 59.4 ± 2.3 | |
| MLVLa | 29 January 2014 | 29 August 2014 | LEICA | GR25 | 3.03 | 37.3 ± 2.8 | −39.8 ± 1.2 | 59.4 ± 2.3 | |
| MLVLa | 29 August 2014 | 20 October 2014 | LEICA | GR25 | 3.10 | 37.3 ± 2.8 | −39.8 ± 1.2 | 59.4 ± 2.3 | |
| MLVLa | 20 October 2014 | 6 August 2016 | LEICA | GR25 | 3.11 | 37.3 ± 2.8 | −39.8 ± 1.2 | 59.4 ± 2.3 | |
| MLVLb | 11 August 2016 | 9 November 2016 | LEICA | GR25 | 3.11 | −28.9 ± 0.7 | −63.0 ± 1.0 | 81.9 ± 2.7 | |
| MLVLb | 9 November 2016 | NOW 1 | LEICA | GR25 | 4.02 | −28.9 ± 0.7 | −63.0 ± 1.0 | 81.9 ± 2.7 | |
| NYA2 | 25 October 2015 | 25 October 2016 | JAVAD | TRE_G3TH DELTA | 3.5.10 | −29.3 ± 0.8 | 18.2 ± 1.6 | 0.6 ± 8.0 | |
| NYA2 | 25 October 2016 | NOW 1 | JAVAD | TRE_G3TH DELTA | 3.6.7 | −29.3 ± 0.8 | 18.2 ± 1.6 | 0.6 ± 8.0 | |
| OBE4 | 25 October 2015 | 17 October 2016 | JAVAD | TRE_G3TH DELTA | 3.5.10 | −31.1 ± 0.7 | 22.3 ± 1.0 | ||
| OBE4 | 17 October 2016 | NOW 1 | JAVAD | TRE_G3TH DELTA | 3.6.7 | −31.1 ± 0.7 | 22.3 ± 1.0 | ||
| PADOa | 1 January 2014 | 25 August 2014 | LEICA | GR10 | 3.00/6.113 | 40.7 ± 4.4 | −41.4 ± 1.3 | 53.2 ± 2.2 | |
| PADOa | 25 August 2014 | 15 March 2016 | LEICA | GR10 | 3.10.1633/6.403 | 40.7 ± 4.4 | −41.4 ± 1.3 | 53.2 ± 2.2 | |
| PADOb | 15 March 2016 | 15 June 2016 | LEICA | GR10 | 3.22/6.521 | −25.3 ± 1.4 | −64.7 ± 0.3 | 77.6 ± 1.8 | |
| PADOb | 15 June 2016 | 24 August 2016 | LEICA | GR10 | 4.00/6.521 | −25.3 ± 1.4 | −64.7 ± 0.3 | 77.6 ± 1.8 | |
| PADOb | 24 August 2016 | NOW 1 | LEICA | GR10 | 4.00/6.522 | −25.3 ± 1.4 | −64.7 ± 0.3 | 77.6 ± 1.8 | |
| PEN2 | 2 March 2015 | NOW 1 | LEICA | GRX1200 + GNSS | 8.51/6.110 | 41.6 ± 2.7 | 54.9 ± 3.5 | ||
| POTS | 2 March 2015 | 15 September 2015 | JAVAD | TRE_G3TH DELTA | 3.4.7 | −21.8 ± 0.8 | 16.8 ± 1.1 | ||
| POTS | 15 September 2015 | 25 October 2016 | JAVAD | TRE_G3TH DELTA | 3.5.10 | −21.8 ± 0.8 | 16.8 ± 1.1 | ||
| POTS | 25 October 2016 | NOW 1 | JAVAD | TRE_G3TH DELTA | 3.6.7 | −21.8 ± 0.8 | 16.8 ± 1.1 | ||
| REDU | 2 March 2015 | 27 August 2015 | SEPTENTRIO | POLARX4 | 2.5.2-esa3 | 0.3 ± 0.4 | 0.0 ± 0.9 | −0.4 ± 1.2 | |
| REDU | 27 August 2015 | 18 October 2016 | SEPTENTRIO | POLARX4 | 2.9.0 | 0.3 ± 0.4 | 0.0 ± 0.9 | −0.4 ± 1.2 | |
| REDU | 18 October 2016 | NOW 1 | SEPTENTRIO | POLARX4 | 2.9.5-extref1 | 0.3 ± 0.4 | 0.0 ± 0.9 | −0.4 ± 1.2 | |
| REYKa | 2 March 2015 | 8 August 2016 | LEICA | GR25 | 3.11.1639/6.403 | 42.8 ± 1.2 | −43.9 ± 0.8 | 62.0 ± 2.4 | |
| REYKb | 8 August 2016 | NOW 1 | LEICA | GR25 | 3.11.1639/6.522 | −24.4 ± 0.7 | −67.0 ± 0.9 | 83.8 ± 3.0 | |
| SULP | 21 June 2015 | 11 November 2016 | TOPCON | NET-G3A | 4.1 31 May 2013 | −76.5 ± 1.3 | |||
| SULP | 16 November 2016 | NOW 1 | TOPCON | NET-G3A | 4.7 23 October 2015 | −76.5 ± 1.3 | |||
| TLSEa | 2 March 2015 | 19 June 2015 | TRIMBLE | NETR9 | 4.85 | 15.9 ± 0.9 | −13.6 ± 1.6 | 43.1 ± 2.1 | |
| TLSEa | 19 June 2015 | 11 March 2016 | TRIMBLE | NETR9 | 5.01 | 15.9 ± 0.9 | −13.6 ± 1.6 | 43.1 ± 2.1 | |
| TLSEb | 11 March 2016 | 11 August 2016 | TRIMBLE | NETR9 | 5.01 | 13.6 ± 0.9 | −14.7 ± 0.6 | 44.8 ± 0.9 | |
| TLSEb | 11 August 2016 | 12 December 2016 | TRIMBLE | NETR9 | 5.14 | 13.6 ± 0.9 | −14.7 ± 0.6 | 44.8 ± 0.9 | |
| TLSEb | 12 December 2016 | 23 May 2017 | TRIMBLE | NETR9 | 5.15 | 13.6 ± 0.9 | −14.7 ± 0.6 | 44.8 ± 0.9 | |
| TLSEb | 23 May 2017 | 15 June 2017 | TRIMBLE | NETR9 | 5.22 | 13.6 ± 0.9 | −14.7 ± 0.6 | 44.8 ± 0.9 | |
| TLSEb | 15 June 2017 | NOW 1 | TRIMBLE | NETR9 | 5.22 | 13.6 ± 0.9 | −14.7 ± 0.6 | 44.8 ± 0.9 | |
| VILL | 25 October 2015 | 21 October 2016 | SEPTENTRIO | POLARX4 | 2.9.0 | 2.1 ± 0.5 | −0.3 ± 0.8 | −0.7 ± 1.1 | |
| VILL | 21 October 2016 | NOW 1 | SEPTENTRIO | POLARX4 | 2.9.5-extref1 | 2.1 ± 0.5 | −0.3 ± 0.8 | −0.7 ± 1.1 | |
| WROCa | 2 March 2015 | 4 September 2015 | LEICA | GR25 | 3.11.1639/6.403 | 63.2 ± 1.4 | 84.7 ± 1.8 | −12.7 ± 18.3 | |
| WROCb | 4 September 2015 | 10 March 2016 | LEICA | GR25 | 3.21/6.403 | 19.8 ± 1.3 | −62.8 ± 0.9 | 72.8 ± 2.1 | −13.5 ± 20.1 |
| WROCb | 10 March 2016 | 14 April 2016 | LEICA | GR25 | 3.22/6.521 | 19.8 ± 1.3 | −62.8 ± 0.9 | 72.8 ± 2.1 | −13.5 ± 20.1 |
| WROCc | 15 April 2016 | 23 May 2016 | LEICA | GR25 | 3.22/6.521 | 12.1 ± 10.1 | −62.4 ± 2.0 | 72.0 ± 9.2 | −14.3 ± 27.2 |
| WROCc | 23 May 2016 | NOW 1 | LEICA | GR25 | 3.22/6.522 | 12.1 ± 10.1 | −62.4 ± 2.0 | 72.0 ± 9.2 | −14.3 ± 27.2 |
| WTZ3a | 25 October 2015 | 23 April 2016 | JAVAD | TRE_G3TH DELTA | 3.6.1b1-68-7da1 | −16.2 ± 1.6 | 20.4 ± 2.6 | ||
| WTZ3b | 28 April 2016 | 12 January 2017 | JAVAD | TRE_G3TH DELTA | 3.6.1b1-68-7da1 | −19.9 ± 0.7 | 19.4 ± 5.1 | ||
| WTZ3b | 12 January 2017 | NOW 1 | JAVAD | TRE_G3TH DELTA | 3.6.9 | −19.9 ± 0.7 | 19.4 ± 5.1 | ||
| WTZZa | 1 January 2014 | 17 April 2014 | JAVAD | TRE_G3TH DELTA | 3.5.3 19 September 2013 | −14.5 ± 1.7 | 169.7 ± 9.4 | ||
| WTZZa | 17 April 2014 | 14 August 2014 | JAVAD | TRE_G3TH DELTA | 3.5.5 3 March 2014 | −14.5 ± 1.7 | 169.7 ± 9.4 | ||
| WTZZa | 14 August 2014 | 27 January 2015 | JAVAD | TRE_G3TH DELTA | 3.6.0 23 June 2014 | −14.5 ± 1.7 | 169.7 ± 9.4 | ||
| WTZZa | 27 January 2015 | 16 June 2015 | JAVAD | TRE_G3TH DELTA | 3.6.1 30 December 2014 | −14.5 ± 1.7 | 169.7 ± 9.4 | ||
| WTZZa | 16 June 2015 | 12 July 2015 | JAVAD | TRE_G3TH DELTA | 3.6.2 8 April 2015 | −14.5 ± 1.7 | 169.7 ± 9.4 | ||
| WTZZb | 13 July 2015 | 20 November 2015 | JAVAD | TRE_G3TH DELTA | 3.6.2 8 April 2015 | −16.3 ± 0.8 | −130.2 ± 3.0 | ||
| WTZZb | 20 November 2015 | 26 November 2015 | JAVAD | TRE_G3TH DELTA | 3.6.3 1 July 2015 | −16.3 ± 0.8 | −130.2 ± 3.0 | ||
| WTZZb | 26 November 2015 | 16 February 2016 | JAVAD | TRE_G3TH DELTA | 3.6.4B1-57-AB7E | −16.3 ± 0.8 | −130.2 ± 3.0 | ||
| WTZZc | 16 February 2016 | 19 May 2016 | JAVAD | TRE_G3TH DELTA | 3.6.4 12 January 2016 | −12.2 ± 1.0 | −133.7 ± 0.8 | ||
| WTZZd | 19 May 2016 | 1 December 2016 | JAVAD | TRE_G3TH DELTA | 3.6.6 27 April 2016 | −15.3 ± 0.6 | −2.6 ± 3.3 | 22.2 ± 0.0 | |
| WTZZe | 2 December 2016 | 12 January 2017 | JAVAD | TRE_G3TH DELTA | 3.6.6 27 April 2016 | −12.7 ± 0.8 | −6.0 ± 1.2 | 18.0 ± 1.9 | |
| WTZZf | 12 January 2017 | 14 February 2017 | JAVAD | TRE_G3TH DELTA | 3.6.9 28 November 2016 | −16.2 ± 0.6 | −3.1 ± 0.8 | 17.5 ± 0.0 | |
| WTZZg | 15 February 2017 | NOW 1 | JAVAD | TRE_G3TH DELTA | 3.6.9 28 November 2016 | −12.3 ± 0.8 | −6.5 ± 1.3 | 17.4 ± 3.0 | |
| ZIMJa | 1 January 2014 | 12 May 2016 | JAVAD | TRE_G3TH DELTA | 3.4.9 18 April 2013 | −20.6 ± 1.9 | 21.9 ± 1.8 | ||
| ZIMJb | 12 May 2016 | NOW 1 | JAVAD | TRE_G3TH DELTA | 3.5.12 12 November 2015 | −24.8 ± 0.7 | 19.3 ± 2.8 | ||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nicolini, L.; Caporali, A. Investigation on Reference Frames and Time Systems in Multi-GNSS. Remote Sens. 2018, 10, 80. https://doi.org/10.3390/rs10010080
Nicolini L, Caporali A. Investigation on Reference Frames and Time Systems in Multi-GNSS. Remote Sensing. 2018; 10(1):80. https://doi.org/10.3390/rs10010080
Chicago/Turabian StyleNicolini, Luca, and Alessandro Caporali. 2018. "Investigation on Reference Frames and Time Systems in Multi-GNSS" Remote Sensing 10, no. 1: 80. https://doi.org/10.3390/rs10010080
APA StyleNicolini, L., & Caporali, A. (2018). Investigation on Reference Frames and Time Systems in Multi-GNSS. Remote Sensing, 10(1), 80. https://doi.org/10.3390/rs10010080