Abstract
An increasing number of satellites of global navigation satellite systems (GNSS) and their constant modernization allow improving positioning accuracy and enable performing the GNSS measurements in challenging environments. Since 2016, the Centre National d’Études Spatiales (CNES) has been providing real-time corrections for all GNSS and thus allows for the actual multi-GNSS precise point positioning in real time without any issues associated with the latency of orbit and clock products as in the case of the IGS final products. We provide a comprehensive evaluation of the availability and the quality of multi-GNSS real-time orbit and clock products through the comparison to the final Center for Orbit Determination in Europe (CODE) orbits, fitting long continuous orbital arcs, analyzing the orbit position differences with respect to satellite laser ranging observations, as well as the assessment of clock stability using modified Allan deviation diagrams. The 3D orbit RMS over a 1-month test period, when compared to CODE products, is 5, 10, 18, 18 and 36 cm for GPS, GLONASS, Galileo, BeiDou MEO and BeiDou IGSO, respectively. The error of BeiDou geostationary orbits is above the 1-m level. Finally, we found that the quality of orbits and clocks is a function of the satellite system, orbital plane and the elevation of the Sun above the orbital plane, the satellite altitude, as well as the satellite block and generation.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
Introduction
Precise point positioning (PPP) is an undifferenced technique that employs a single GNSS receiver (Zumberge et al. 1997). PPP takes advantage of precise satellite clocks and orbits that are considered fixed parameters in the normal equation system. As PPP has been dynamically developed over the years (Choy et al. 2017), it is necessary to use as accurate products as possible in order to avoid error propagation and to fully exploit the PPP potential. Thus, the user must fully rely on the quality of the orbits and clocks provided. The primary application of PPP is coordinate determination. Another application field is space weather monitoring (Lu et al. 2015), the estimation of the zenith total delay to support numerical weather prediction models (Dousa and Vaclavovic 2014) or detecting earthquakes or tsunamis (Collins et al. 2009, Li et al. 2013).
Multi-GNSS
The International GNSS Service (IGS) provides precise products for GPS and GLONASS, but also intends to support the remaining constellations (Dow et al. 2009). For this purpose, the IGS Multi-GNSS experiment (MGEX) was established, which tracks, collates and analyzes all available GNSS signals. GNSS analysis centers (ACs) which take part in MGEX provide products that allow the use of a greater number of satellites. Among the mentioned centers are Centre National d’Études Spatiales (CNES, Loyer et al. 2012) and Center for Orbit Determination in Europe (CODE, Dach et al. 2015a). In order to satisfy real-time (RT) user needs, the IGS Real-Time Service (IGS-RTS), providing GPS and GLONASS products, has been launched in 2013; its product quality has been assessed by Hadas and Bosy (2015). Unfortunately, multi-GNSS products provided by single AC are not screened for outliers, as opposed to the combined RTS products. Therefore, they should be appropriately verified and validated.
Goal of this study
In recent research, the quality of IGS MGEX products has been evaluated, e.g., Steigenberger et al. (2013, 2015), Steigenberger and Montenbruck (2017). However, there is no current literature devoted to the assessment of the multi-GNSS products for RT users. We fill up this gap by providing a comprehensive evaluation of the RT orbits and clock corrections. We evaluate the quality of RT orbits using three complementary methods: (1) comparison with the post-processing MGEX products, (2) analysis of orbit discontinuities through fitting long and continuous arcs and (3) comparison through the independent satellite laser ranging (SLR) technique. The clocks are evaluated by: (1) comparison with the post-processing MGEX products and (2) modified Allan deviation (MDEV) diagram analysis of the clock stability in various frequency ranges (Allan and Barnes 1981). At the end, positioning tests are performed to check the position accuracy obtained using products being analyzed.
Characteristics of new GNSS
In-orbit validation (IOV) satellites and full operational capability (FOC) satellites, distributed nominally over three orbital planes, can be recognized in the Galileo constellation. BeiDou employs three orbit types: medium earth orbits (MEO), geostationary (GEO) and inclined geosynchronous orbit (IGSO). Thus, BeiDou orbits have two different orbital revolution periods. Nominally, there are three MEO, one GEO and three IGSO orbital planes. Table 1 summarizes the current status of Galileo and BeiDou constellation with pseudo-random noise (PRN), satellite vehicle number (SVN), a satellite type, an orbital plane identifier, a semi-major axis a, an inclination angle i and an eccentricity e for Galileo and BeiDou.
Methodology
We assess availability and quality of RT orbit and clock corrections provided by CNES in April 2016 (DoY 92-121). We use BNC software (Weber and Mervart 2009) to decode correction streams from Radio Technical Commission for Maritime Services—RTCM. RT satellite orbits and clocks are calculated using an in-house developed GNSS-WARP software (Hadas 2015). For the orbit validation employing SLR observations, we use Bernese GNSS software (Dach et al. 2015b).
Issue of data (IOD) matching
Joining RT correction with respective ephemerides has to be done using IOD number that allows for identifying the ephemeris. The IOD number for GPS and Galileo ephemeris is directly provided in the message as opposed to GLONASS and BeiDou. Therefore, the methodology of IOD calculation for GLONASS and BeiDou derived from the BNC source code is introduced in the following subsections.
GLONASS IOD calculation
The procedure for GLONASS IOD calculation is based on the ephemeris epoch record. The ephemeris seconds of day (SoD) in UTC are computed from time of clock parameters: hour, minute and second. Then, UTC SoD are converted to Moscow time (MT). Finally, the IOD is calculated as:
The GLONASS IOD may thus be interpreted as the number of 15-min intervals in a day for MT.
BeiDou IOD calculation
In order to calculate IOD for BeiDou, three clock correction parameters and 15 ephemeris parameters should be involved. The parameters are divided by the scale factor and are converted from decimal to binary format taking into account the number of pre-allocated bits (BeiDou ICD 2013). Next, the parameters are stacked into one binary string in the following order: IDOT, a 2, a 1, a 0, C rs, Δn, M 0, C uc, e, C us, \( \sqrt A \), C ic, \( \varOmega_{0} \), C is, i 0, C rc, ω, \( \dot{\varOmega } \), where symbols are compatible with BeiDou ICD. Then, five zero bits are added at the end of the binary string to divide the string into bytes. Finally, BeiDou IOD is calculated as a control sum CRC-24 of the obtained 52 bytes.
Availability of real-time corrections
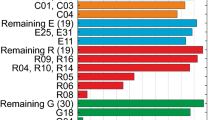
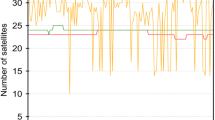
The availability of precise corrections influences the positioning precision and solution stability. Therefore, RT orbit and clock correction availability was first checked (Fig. 1).
We can classify unavailability events into several groups: (1) permanent (e.g., G04), (2) temporal (e.g., R01) unavailability period of some satellites, (3) epochs without corrections only for some systems (e.g., DoY 94 for BeiDou) and (4) epochs without corrections for all satellites (vertical bands in Fig. 1). Groups (1) and (2) originate from corrections not provided (e.g., E08). Missing corrections may refer to scheduled maneuvers conducted for the selected satellites. The gap for G32 at the beginning of the test period is connected with the satellite replacement for the slot G32 from block IIA for a block IIF in February 2016. For satellites E08 and E09, there were some problems with the correction calculation related to a short time span since their launch in December 2015. An analogous situation exists for R09, R16 and R17, all of which were launched shortly before the beginning of the test period (February/March 2016). Missing corrections from the group (3) may relate to incomplete data streams. Gaps, e.g., in DoY 94 for BeiDou, refer to wrong dates in correction headers in the files saved by BNC. Those errors correspond to the BNC issues or mismatches in the transmitted streams.
The overall availability median for all the systems reaches 90% when excluding BeiDou. The smallest number of corrections for BeiDou is mainly related to previously described correction message errors (Table 2).
Quality assessment
The process of quality assessment for the test period splits into four independent parts: comparison with the final CODE MGEX products, assessment based on fitted continuous daily arcs, comparison with SLR observations and clock analysis using MDEV.
Orbit and clock comparison to the final products
As a reference product, the final CODE MGEX (Prange et al. 2017) solution is employed. It provides both the orbits and clocks for GPS, GLONASS, Galileo and BeiDou excluding BeiDou GEO satellites, of which the latter are associated with a poor accuracy of their orbits (Steigenberger et al. 2013). The CODE orbits are based on double-difference solutions employing the ionospheric-free linear combination of two selected signals, whereas the CODE clocks are based on undifferenced PPP solutions with fixed orbits.
Quality of orbit products
The orbit comparison is done in 15-min intervals for three components: radial, along-track and cross-track. Clocks are aligned using median calculated for each epoch and system separately. Outliers are removed using a threshold of 2.5 standard deviations (SD) of the analyzed data set. Figure 2 shows the differences between RT and the final orbits and clocks. The satellites are grouped according to the occupied orbital plane. Numerical statistics are also computed for each satellite block and the system assignment (Table 3). This distinction allows for checking whether there are any dependencies between the product accuracy and satellite types, blocks or orbital planes.
The most accurate orbits are for GPS with the SD of residuals equal 2.3, 3.2 and 2.8 cm for the radial, along- and cross-track component, respectively. The radial component of GLONASS has a slightly lower accuracy than the radial component of GPS. The accuracy of other systems is at least twice worse than of GPS. The 3D SD of residuals is 4.8, 9.8, 18.3 and 28.2 cm for GPS, GLONASS, Galileo and BeiDou, respectively.
The quality of GPS orbit positions is not related to the orbital plane and the satellite block (Fig. 2 and Table 3). Satellite block dependency may be confirmed only by the satellites from block IIF which have SD bigger by about 0.5 cm than from other blocks for the radial and along-track components.
The GLONASS satellite positions from the orbital plane #1 obtained larger SD than GLONASS satellites from the orbital planes #2 and #3, by about 63, 60 and 27% for the radial, along-track and cross-track component, respectively. The number of outliers is about two times greater for plane #1 than for planes #2 and #3. This may refer to the lowest sun elevation angle above the orbital plane (β) that is in the range from − 5.0° to 25.2° in the test period for the orbit #1 which is related to larger orbit modeling errors for eclipsing satellites (Sośnica et al. 2015). For only one GLONASS-K, R09, the errors are slightly lower than for GLONASS-M; however, it is hard to reliably assess a relationship between satellite type and RT orbit accuracy.
The quality of along-track and cross-track components of Galileo orbit differences is comparable with SD equal about 12 cm, while for the radial component SD is about 6.5 cm. However, the radial component of Galileo has a bigger bias than the remaining components and equals 2.3 cm, which is related to different albedo, and antenna thrust modeling in CODE and CNES. Galileo orbit quality is independent of the occupied orbital plane, analogously to GPS. The significant bias is positive in radial, both for planes A and B, while in cross-track the bias is negative for A and C and positive for B. Table 3 shows that IOV satellites obtain slightly worse position accuracy and a bigger bias than FOC satellites. This can be caused by the fact that CODE employs the new Empirical CODE Orbit Model (ECOM2, Arnold et al. 2015), whereas CNES products employ the classical ECOM1, which may cause a bias in cross-track component (Montenbruck et al. 2017).
The orbital plane BeiDou IGSO B has the worst performance among all IGSO planes. Satellites from the plane IGSO B have SD about 25, 34 and 36 cm for the radial, along- and cross-track components, respectively, which is four, two and two times bigger than the corresponding components of IGSO planes C and D. BeiDou MEO satellites obtain slightly lower SD than IGSO from the orbital planes C and D, however, with a 4-cm bias for cross-track in the plane E and for along-track in the plane F. Other satellites have biases below 2 cm, excluding IGSO in the plane B for which the bias is equal to about 7 cm for the along-track component. These differences are strongly related to a satellite type rather than to the occupied orbital plane. Moreover, IGSO satellites obtain lower SD for the along-track than for the cross-track component, which is unique in comparison with other satellites.
Quality of clock products
GPS clock accuracy is not related to the orbital plane. There are three pairs of orbits with a bias equal 1.2, 0.5 and 0.7 cm for the pairs A–F, B–D and C–E, respectively. The clock analysis introduces a distinction between satellite blocks. GPS block IIF has slightly less accurate clocks with SD equal 3.3 cm, while the remaining blocks obtain almost identical SD of about 2.4 cm with a bias independent from a satellite block. GLONASS clocks have comparable SD. However, there are some GLONASS satellites with bigger SD of clock residuals. The GLONASS satellite orbit quality is also slightly dependent on the orbital plane as SD equal 6.5, 8.2 and 8.6 cm for the orbital planes #1, #2 and #3, respectively. Galileo clocks have SD lower than 10 cm, and the bias is about − 3 cm. E08 and E09 are the only Galileo satellites with bigger SD equal about 12 cm, but their bias is lower than 1 cm. Galileo clocks, excluding the recently operational E08 and E09, are almost as accurate as those for GLONASS, however, with SD bigger by about 1 cm. BeiDou RT clocks are only slightly worse than the Galileo clocks. Two IGSO satellites from the orbital plane B have SD equal 14 cm. This outcome is similar to the orbit results obtained for this orbital plane. Considering BeiDou MEO satellite type, the satellites have a 0.5-cm bias which is three times smaller than the IGSO bias.
Summary
Compared to the final CODE MGEX products (Fig. 3), GPS and GLONASS obtain the best orbital accuracy. Satellite orbits are significantly more accurate for BeiDou MEO than for BeiDou IGSO. The radial component of BeiDou MEO obtains SD equal 4.8 cm which is lower than of Galileo orbits with SD of 6.5 cm, while SD for cross-track is about 12 cm for both.
Fitting continuous orbital arcs
The RT orbit products provided by CNES are based on GNSS observations used to generate orbit and clock predictions for a certain interval. The orbit predictions may thus contain some discontinuities at the boundaries of the prediction intervals. We fit the orbit positions from RT products to daily continuous arcs as another way of orbit validation.
For the orbit fit, ECOM2 is used with the estimation of nine empirical parameters with no stochastic pulses. We fit continuous orbital arcs into the set of satellite positions which provide information on satellite orbit discontinuities at epochs in which new orbit predictions are generated. Daily continuous arcs are adjusted to all days of the analyzed period. Residuals of this fitting procedure for DoY 98, 2016 are shown in Fig. 4. For all systems, there is a visible subcentimeter noise in each component which is related to the last valid digit of data in SP3 files that equals 1 mm. Moreover, some discontinuities appear while fitting arcs into the series of satellite positions. For GPS, GLONASS and BeiDou MEO, discontinuities reach up to 6 cm. For Galileo and BeiDou IGSO satellites, discontinuities are greater, especially for the along-track component. Among all systems, the biggest discontinuities occur for BeiDou GEO and reach up to even 6 m. The biggest discontinuities for particular systems appear with about 6-h intervals for GPS and GLONASS and with 3-h intervals for Galileo and BeiDou which is connected with AC orbit prediction periods. The substantial discontinuities for GEO may be related to an inferior quality of orbit models for GEO satellites. They are in a deep 1:1 orbit resonance with the earth’s gravity field (Hugentobler 1998), where a small change of external forces acting on a satellite causes substantial changes of a satellite position. The quality of BeiDou GEO is thus much worse than of MEO or IGSO (Tan et al. 2016).
GPS fitting residuals assume SD of 1.5 cm for all components with a 0.9-cm bias only for the radial. The accuracy of orbit fitting for GPS is very similar for all days with the SD up to 1.8 cm and the bias of about 1 cm for the radial component. The systematic bias for the radial component can be explained by different modeling of the satellite antenna thrust at CNES and in Bernese software, which corresponds to about 1 cm (Fritsche et al. 2014). The SD of fitting residuals for GLONASS reaches up to about 3 cm for the along-track component, while for two other components SD is below 2 cm. However, there is also a bias for both, radial and along-track components (Table 4). GLONASS-K results are comparable to GPS. For the GLONASS plane #1, which has a mean value of the β-angle equal 10.1° in the considered period, the fitting residuals are greater than those for satellites from planes #2 and #3 with the mean β-angle equal 45.8° and 51.8°, respectively. The bad quality of GLONASS orbits from plane #1 is the reason for the greater overall GLONASS SD and the additional bias for the along-track component (Table 4). Residuals for planes #2 and #3 are, however, comparable with those for GPS with the values at the level of 1.0–1.5 cm.
SD of residuals for Galileo is about 3–4 cm and has a significant cross-track bias. Statistics for BeiDou are worse than for the other systems by an order of magnitude with the SD up to about 70 cm, which is caused mostly by GEO satellites with the largest SD. GEO satellites show a bias of about 12 cm in the cross-track direction. One BeiDou GEO, C04, has the greatest bias for the cross-track component equaling to about − 45 cm. BeiDou MEO satellites are fitted with a quality of about 3–4 cm, which is comparable to Galileo satellites.
Orbit validation using SLR
All satellites, except for GPS, are equipped with laser retroreflectors that enable preforming high-precision distance measurements between ground stations and satellites. Thus, SLR technique is used as an independent source of information on orbit quality and reference data information provided by the International Laser Ranging Service (ILRS) (Pearlman et al. 2002). Due to the lack of SLR observations or a low number thereof, in this step 33 satellites were considered. Figure 5 and Table 5 provide results from the SLR validation.
The SD of SLR residuals for GLONASS is about 4 cm. The residuals to Galileo are twice larger than those to GLONASS, whereas BeiDou satellites show significantly greater SD of SLR residuals equaling to about 50 cm. The GLONASS-K satellite obtains two times smaller SD of SLR residuals, at the level of 2 cm, with the same number of outlaying observations, i.e., about 7%. It may be related to the fact that the GLONASS-K is equipped with a ring-shaped retroreflector construction, as opposed to GLONASS-M satellites, which are equipped with the rectangular retroreflectors (Sośnica et al. 2015).
GLONASS satellites from plane #1 have SLR residuals of about 5 cm, which are the largest of all GLONASS planes, whereas GLONASS satellites from plane #3 achieve the lowest SLR residuals, not exceeding 3 cm. An analogous situation could be observed for the comparison between RT CNES and the CODE final products. The SLR residuals obtained for Galileo satellites from planes A and C are at the level of 11–12 cm and thus are about two times greater than those from the plane B with the SD of 5 cm. The number of SLR observations to satellites occupying planes A and C amounting to 200–300 is lower than for that from plane B, which contains almost 800 observations, which is strictly connected with the number of active Galileo satellites that occupy different orbital planes and with the ILRS tracking priorities. For the BeiDou GEO satellite C01, the SLR residuals assume the largest values between − 200 and + 150 cm with the SD of almost 100 cm. The IGSO C08 has two times greater SD than the IGSO C10. Satellite C08 also has a negative bias that reaches about 5.5 cm. The IGSO C10 obtains almost the same SD as the MEO C11 at the level of 4 cm, which is similar to GLONASS satellites (Table 5).
Results of RT orbit validation using SLR are mainly within the boundaries determined by the SLR validation of the final products obtained by Montenbruck et al. (2017). The SD of SLR residuals for RT orbits is lower than for the final orbits by several millimeters for GLONASS and BeiDou IGSO, while SD for BeiDou GEO is even three times greater than the values for the final products.
Assessment of clock stability using MDEV
The stability of GNSS clocks is analyzed using MDEV, which is commonly employed for the assessments of clock quality (Hauschild et al. 2013, Steigenberger et al. 2015). Figure 6 shows MDEV calculated for all satellites. The initial stability for time integration τ = 30 s is in the range 1.25–3.85 × 10−12, 5.28–9.38 × 10−12, 1.73–1.80 × 10−12 and 2.72–5.38 × 10−12 for GPS, GLONASS, Galileo and BeiDou, respectively.
MDEV for GPS clocks decreases for the time integration from 30 s to about 1000 s and then slightly increases to achieve a local maximum at τ of about 10,000 s, which corresponds to about one fourth of the GPS orbital period. For τ longer than 10,000 s, the MDEV diagram becomes smaller again. The best clock performance out of all GPS satellites is for the block IIF, which is equipped with the Rubidium Atomic Frequency Standards. For G08 and G24 from the block IIF, the MDEV values initially do not vary from IIR satellites, but for τ of about 400 s they show a worse stability than other GPS satellites. Galileo satellites show a comparable clock stability to GPS. The local maximum for the majority of Galileo satellites analyzed occurs for τ of about 12 000 s which is related to one fourth of the Galileo orbital period. However, E24 is an exception among all Galileo satellites, with a local maximum for τ equal to 6000 s.
GPS and Galileo, and GLONASS and BeiDou show comparable results regarding the MDEV analysis. The main advantage of Galileo is the clock homogeneity of all satellites; however, two Galileo satellites have a slightly worse stability at the second half of the considered day. GLONASS has the most consistent internal stability between clocks of different spacecrafts, but they are characterized by about four to five times lower stability than the Galileo and best GPS clocks. MDEV for GLONASS clocks is homogenous with a local maximum for the τ equal to about 12 000 s, i.e., one third of the GLONASS orbital period. Additionally, there is a problem with the GLONASS-K satellite which shows an anomalistic bump for the τ of 200 s.
The clock stability of BeiDou is comparable for all satellites, irrespectively of the orbit type. The only exception is the geostationary satellite C01 for which the clock stability is slightly worse than for other BeiDou clocks. Thus, it cannot be concluded that GEO clocks are less stable than the clocks of other BeiDou satellite types. Additionally, MEO C14 obtains a bump for τ equal to about 2000 s, while the IGSO C06 misbehaves at the longest integration and shows a bump around τ = 13 000 s. The remaining BeiDou MEO performs better for longer integration periods without any prominent bumps.
Validation using PPP
We run positioning tests for DoY 120, 2016 to check the correction contribution to range errors under actual processing conditions for eleven multi-GNSS IGS stations (Fig. 7). Tests were conducted in five variants: GPS (G), GPS + GLONASS (G + R), GPS + Galileo (G + E), GPS + BeiDou (G + C) and a combination of all available systems for each station named G + R + E + C. For the static mode, we provide coordinate differences and their formal errors. For the kinematic mode, we present the daily mean absolute coordinate differences and daily mean formal errors. As reference coordinates both in static and in the kinematic modes, we use IGS weekly combined solutions.
The inclusion of another system to GPS mainly reduces formal coordinate errors by 7–36%, depending on the component (Table 6). The lowest improvement is in G + E, where the reduction in formal errors does not exceed 20%. G + R + E + C reduces formal errors for all components by more than 30% which refers to the improved observation geometry. The improvement could possibly be better when applying an optimized weighing for individual GNSS.
The bias in the static mode is mainly reduced for the east component by 10% when excluding G + E, in which the bias is larger than in G by about 15%. In G + C for the up component, the mean bias is smaller and larger by about 10% for G + C and G + E when compared to G in the static mode, respectively. The bias of the north component is similar in four variants without G + C with differences up to 3% and is slightly bigger by 7% in G + C. In the kinematic mode, the bias is reduced only in the G + R variant by 15 and 6% for the north and east components, respectively. In other variants, biases are bigger by about 6–20%. For the up component, the bias is reduced for all variants by about 6–12%. The only exception is the G + C variant where the bias for the up component is slightly bigger than in G by 4%.
Figure 8 illustrates formal errors from the static mode for the all tested variants. Adding GLONASS typically reduces errors for all components on average by 21–25%. Additional observations provided by Galileo reduce formal errors by about 12–16%, which is lower than for other systems. In the case of the G + C variant, the biggest error decrease is visible for stations located in the Asia-Pacific region and reaches between 21 and 37%. For stations observing only MEO or GEO and IGSO satellites at low elevation angles, the reduction in formal errors in G + C is not as big as in case of G + R due to a limited number of epochs with BeiDou observations and no observations in zenith (e.g., for WROC).
Conclusions
We assessed the availability and the accuracy of RT multi-GNSS products provided by CNES. Availability of products for GPS, GLONASS and Galileo is at a satisfactory level and exceeds 90% in the test period. Gaps in the product availability are mainly caused by the problems with the Internet connection on the user side. Another reason for missing RT data is a problem with IOD matching at the level of data processing. Authors are aware of the fact that the availability assessment is not absolute and may be affected by other error sources.
The RMSE for RT-IGS is similar to the results obtained when compared to the final products and ranges from 3 to 5 cm and from 1.5 to 4.0 cm for GPS orbits and clocks, respectively. Results obtained for GPS orbits and clocks are comparable to those presented on the RT-IGS website http://www.igs.org/rts/monitor.
The accuracy of GPS satellite orbits compared to CODE MGEX is the highest and reaches the level of about 3 cm for position components. GLONASS orbits are not as accurate as those estimated for GPS, especially for the along- and cross-track orbit components with SD equal to 8 and 6 cm, respectively. It is partly dependent on the low β angle for the GLONASS orbital plane #1 and partly with insufficiently accurate models for GLONASS and different behavior of these satellites. Galileo orbits have the accuracy at the decimeter level which is comparable to BeiDou MEO satellites. There are still some modeling errors for GEO and IGSO for which the results are inferior with respect to MEO. Although the results obtained from the comparison with SLR are slightly different, the order of the system accuracy is the same: The most accurate is GLONASS, while the least accurate is BeiDou, especially GEO satellite orbits.
The GPS clocks with SD equal to about 3 cm obtain the best performance compared to the all analyzed systems from the comparison between the final and RT products. GLONASS and Galileo clock differences do not exceed 10 cm, while BeiDou clocks have SD equal about 11 cm.
Galileo clocks are most stable in short periods which may be strictly related to the clock accuracy installed on the spacecraft. The newest GPS IIF generation is characterized by similar MDEV as Galileo, however, with a higher stability for longer integration time in the case of GPS. The variety of GPS clocks is connected with differences between satellite generations. The presented results confirm that BeiDou and GLONASS clocks have a comparable level of stability which is noticeably worse than for GPS and Galileo. The quality of products is not only connected with a system, but also with other factors which are either stable, such as the spacecraft construction, or vary in time, e.g., the β angle.
The positioning tests indicate that additional systems mainly reduce the formal errors mostly due to the improved observation geometry. However, the mean biases become sometimes even larger when adding Galileo or especially BeiDou in the kinematic positioning. The results obtained are especially important for potential users of RT products. The results presented may thus form a background for further analyses that will be focused on appropriate observation weighting for the RT PPP processing using multi-GNSS data.
References
Allan DW, Barnes JA (1981) A modified “Allan variance” with increased oscillator characterization ability. In: Thirty fifth annual frequency control symposium, pp 470–475. IEEE
Arnold D, Meindl M, Beutler G, Dach R, Schaer S, Lutz S, Prange L, Sośnica K, Mervart L, Jäggi A (2015) CODE’s new solar radiation pressure model for GNSS orbit determination. J Geod 89(8):775791. https://doi.org/10.1007/s00190-015-0814-4
BeiDou ICD (2013) BeiDou navigation satellite system signal. Space Interface Control Document. Open Service Signal
Choy S, Bisnath S, Rizos C (2017) Uncovering common misconceptions in GNSS precise point positioning and its future prospect. GPS Solut 21(1):13–22. https://doi.org/10.1007/s10291-016-0545-x
Collins P, Henton J, Mireault Y, Heroux P, Schmidt M, Dragert H, Bisnath S (2009). Precise point positioning for real-time determination of co-seismic crustal motion. In: Proceedings of ION GNSS 2009, Institute of Navigation, Savannah, Georgia, USA, September 22–25, pp 2479–2488
Dach R et al (2015a) CODE analysis center technical report 2014. International GNSS service: technical report 2014, Dach R, Jean Y (eds) (AIUB), IGS Central Bureau, p 2134. https://doi.org/10.7892/boris.80306
Dach R, Lutz S, Walser P, Fridez P (eds) (2015b) Bernese GNSS software version 5.2. User manual. Astronomical Institute, University of Bern, Bern Open Publishing. https://doi.org/10.7892/boris.72297
Dousa J, Vaclavovic P (2014) Real-time zenith tropospheric delays in support of numerical weather prediction applications. Adv Space Res 53(9):1347–1358. https://doi.org/10.1016/j.asr.2014.02.021
Dow J, Neilan R, Rizos C (2009) The International GNSS Service in a changing landscape of global navigation satellite systems. J Geod 83(34):191198. https://doi.org/10.1007/s00190-008-0300-3
Fritsche M, Sosnica K, Rodríguez-Solano C, Steigenberger P, Wang K, Dietrich R, Dach R, Hugentobler U, Rothacher M (2014) Homogeneous reprocessing of GPS, GLONASS and SLR observations. J Geod 88(7):625–642. https://doi.org/10.1007/s00190-014-0710-3
Hadas T (2015) GNSS-Warp software for real-time precise point positioning. Artif Satell 50(2):59–76. https://doi.org/10.1515/arsa-2015-0005
Hadas T, Bosy J (2015) IGS RTS precise orbits and clocks verification and quality degradation over time. GPS Solut 19(1):93–105. https://doi.org/10.1007/s10291-014-0369-5
Hauschild A, Montenbruck O, Steigenberger P (2013) Short-term analysis of GNSS clocks. GPS Solut 17(3):295–307. https://doi.org/10.1007/s10291-012-0278-4
Hugentobler U (1998) Astrometry and satellite orbits: theoretical considerations and typical applications. Geodätisch-geophysikalische Arbeiten in der Schweiz, vol 57. Swiss Geodetic Commission
Li X, Ge M, Zhang Y, Wang R, Xu P, Wickert J, Schuh H (2013) New approach for earthquake/tsunami monitoring using dense GPS networks. Sci Rep 3:2682. https://doi.org/10.1038/srep02682
Loyer S, Perosanz F, Mercier F, Capdeville H, Marty JC (2012) Zero difference GPS ambiguity resolution at CNES-CLS IGS Analysis Center. J Geod 86(11):991–1003. https://doi.org/10.1007/s00190-012-0559-2
Lu C, Li X, Ge M, Heinkelmann R, Nilsson T, Soja B, Dick G, Schuh H (2015) Estimation and evaluation of real-time precipitable water vapor from GLONASS and GPS. GPS Solut 20(4):703–713. https://doi.org/10.1007/s10291-015-0479-8
Montenbruck O et al (2017) The Multi-GNSS experiment (MGEX) of the international GNSS service (IGS)—achievements, prospects and challenges. Adv Space Res 59(7):1671–1697. https://doi.org/10.1016/j.asr.2017.01.011
Pearlman MR, Degnan JJ, Bosworth JM (2002) The international laser ranging service. Adv Space Res 30(2):135–143. https://doi.org/10.1016/S0273-1177(02)00277-6
Prange L, Orliac E, Dach R, Arnold D, Beutler G, Schaer S, Jäggi A (2017) CODE’s five-system orbit and clock solution—the challenges of multi-GNSS data analysis. J Geod 91(4):345–360. https://doi.org/10.1007/s00190-016-0968-8
Sośnica K, Thaller D, Dach R, Steigenberger P, Beutler G, Arnold D, Jaeggi A (2015) Satellite laser ranging to GPS and GLONASS. J Geod 89(7):725–743. https://doi.org/10.1007/s00190-015-0810-8
Steigenberger P, Montenbruck O (2017) Galileo status: orbits, clocks, and positioning. GPS Solut 21(2):319–331. https://doi.org/10.1007/s10291-016-0566-5
Steigenberger P, Hugentobler U, Hauschild A, Montenbruck O (2013) Orbit and clock analysis of Compass GEO and IGSO satellites. J Geod 87(6):515525. https://doi.org/10.1007/s00190-013-0625-4
Steigenberger P, Hugentobler U, Loyer S, Perosanz F, Prange L, Dach R, Uhlemann M, Gendt G, Montenbruck O (2015) Galileo orbit and clock quality of the IGS Multi-GNSS Experiment. Adv Space Res 55(1):269281. https://doi.org/10.1016/j.asr.2014.06.030
Tan B, Yuan Y, Zhang B, Hsu HZ, Ou J (2016) A new analytical solar radiation pressure model for current BeiDou satellites: IGGBSPM. Sci Rep 6:32967. https://doi.org/10.1038/srep32967
Weber G, Mervart L (2009) The BKG Ntrip Client (BNC). In: Report on EUREF symposium 2007 in London, vol 42. Mitteilungen des Bundesamtes fuer Kartographie und Geodaesie
Zumberge JF, Heflin MB, Jefferson DC, Watkins MM, Webb FH (1997) Precise point positioning for the efficient and robust analysis of GPS data from large networks. J Geophys Res Solid Earth 102(B3):5005–5017. https://doi.org/10.1029/96JB03860
Acknowledgements
This work has been supported by the Polish National Science Center (2014/15/B/ST10/00084) and the Wroclaw Center of Networking and Supercomputing (http://www.wcss.wroc.pl/, computational Grant using MATLAB software License No: 101979). We acknowledge the Centre National d’Études Spatiales (CNES) for providing real-time streams, Center for Orbit Determination in Europe (CODE) for the final products, the Bundesamt für Kartographie und Geodäsie (BKG) for providing the open-source BNC software, the ILRS for providing SLR data.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Kazmierski, K., Sośnica, K. & Hadas, T. Quality assessment of multi-GNSS orbits and clocks for real-time precise point positioning. GPS Solut 22, 11 (2018). https://doi.org/10.1007/s10291-017-0678-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10291-017-0678-6