Summary
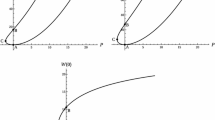
The dual solutions to an equation, which arose previously in mixed convection in a porous medium, occuring for the parameter α in the range 0 < α < α0 are considered. It is shown that the lower branch of solutions terminates at α=0 with an essential singularity. It is also shown that both branches of solutions bifurcate out of the single solution at α=0 with an amplitude proportional to (α0-α)1/2. Then, by considering a simple time-dependent problem, it is shown that the upper branch of solutions is stable and the lower branch unstable, with the change in temporal stability at α=α0 being equivalent to the bifurcation at that point.
Similar content being viewed by others
References
J.H. Merkin, Mixed convection boundary layer flow on a vertical surface in a saturated porous medium,J. Engng. Math. 14 (1980) 301–313.
S.N. Brown and K. Stewartson, On the reversed flow solutions of the Falkner-Skan equation,Mathematika 13 (1966) 1–6.
D.R. Chapman, Laminar mixing of a compressible fluid, NACA Rep. 958 (1950).
D.B. Ingham, J.H. Merkin and I. Pop, The collision of free-convection boundary layers on a horizontal cylinder embedded in a porous medium,Q. J1. Mech. Appl. Math. 36 (1983) 313–335.
L.J. Slater,Confluent hypergeometric functions, Cambridge University Press (1960).
J.H. Merkin, On solutions of the boundary-layer equations with algebraic decay,J. Fluid Mech. 88 (1978) 309–321.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Merkin, J.H. On dual solutions occurring in mixed convection in a porous medium. J Eng Math 20, 171–179 (1986). https://doi.org/10.1007/BF00042775
Received:
Issue Date:
DOI: https://doi.org/10.1007/BF00042775