Published online by Cambridge University Press: 20 November 2018
Let 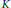 $K$ be a real quadratic field, and
$K$ be a real quadratic field, and 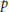 $p$ a rational prime which is inert in
$p$ a rational prime which is inert in 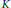 $K$. Let
$K$. Let 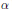 $\alpha $ be a modular unit on
$\alpha $ be a modular unit on 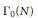 ${{\Gamma }_{0}}(N)$. In an earlier joint article with Henri Darmon, we presented the definition of an element
${{\Gamma }_{0}}(N)$. In an earlier joint article with Henri Darmon, we presented the definition of an element 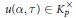 $u\left( \alpha ,\,\text{ }\!\!\tau\!\!\text{ } \right)\,\in \,K_{P}^{\times }$ attached to
$u\left( \alpha ,\,\text{ }\!\!\tau\!\!\text{ } \right)\,\in \,K_{P}^{\times }$ attached to 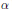 $\alpha $ and each
$\alpha $ and each 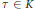 $\tau \,\in \,K$. We conjectured that the
$\tau \,\in \,K$. We conjectured that the 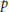 $p$-adic number
$p$-adic number 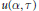 $u(\alpha ,\,\tau )$ lies in a specific ring class extension of
$u(\alpha ,\,\tau )$ lies in a specific ring class extension of 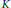 $K$ depending on
$K$ depending on 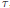 $\tau $, and proposed a “Shimura reciprocity law” describing the permutation action of Galois on the set of
$\tau $, and proposed a “Shimura reciprocity law” describing the permutation action of Galois on the set of 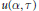 $u(\alpha ,\,\tau )$. This article provides computational evidence for these conjectures. We present an efficient algorithm for computing
$u(\alpha ,\,\tau )$. This article provides computational evidence for these conjectures. We present an efficient algorithm for computing 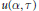 $u(\alpha ,\,\tau )$, and implement this algorithm with the modular unit
$u(\alpha ,\,\tau )$, and implement this algorithm with the modular unit 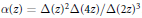 $\alpha (z)\,=\,\Delta {{(z)}^{2}}\,\Delta (4z)\,/\,\Delta {{(2z)}^{3}}$. Using
$\alpha (z)\,=\,\Delta {{(z)}^{2}}\,\Delta (4z)\,/\,\Delta {{(2z)}^{3}}$. Using 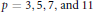 $p\,=\,3,\,5,\,7\,and\,11$, and all real quadratic fields
$p\,=\,3,\,5,\,7\,and\,11$, and all real quadratic fields 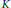 $K$ with discriminant
$K$ with discriminant 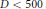 $D\,<\,500$ such that 2 splits in
$D\,<\,500$ such that 2 splits in 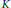 $K$ and
$K$ and 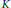 $K$ contains no unit of negative norm, we obtain results supporting our conjectures. One of the theoretical results in this paper is that a certain measure used to define
$K$ contains no unit of negative norm, we obtain results supporting our conjectures. One of the theoretical results in this paper is that a certain measure used to define 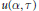 $u(\alpha ,\,\tau )$ is shown to be
$u(\alpha ,\,\tau )$ is shown to be 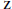 $\mathbf{Z}$-valued rather than only
$\mathbf{Z}$-valued rather than only 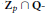 ${{\mathbf{Z}}_{P}}\,\cap \,\mathbf{Q}-$valued; this is an improvement over our previous result and allows for a precise definition of
${{\mathbf{Z}}_{P}}\,\cap \,\mathbf{Q}-$valued; this is an improvement over our previous result and allows for a precise definition of 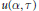 $u(\alpha ,\,\tau )$, instead of only up to a root of unity.
$u(\alpha ,\,\tau )$, instead of only up to a root of unity.
To send this article to your Kindle, first ensure no-reply@cambridge.org is added to your Approved Personal Document E-mail List under your Personal Document Settings on the Manage Your Content and Devices page of your Amazon account. Then enter the ‘name’ part of your Kindle email address below. Find out more about sending to your Kindle. Find out more about saving to your Kindle.
Note you can select to save to either the @free.kindle.com or @kindle.com variations. ‘@free.kindle.com’ emails are free but can only be saved to your device when it is connected to wi-fi. ‘@kindle.com’ emails can be delivered even when you are not connected to wi-fi, but note that service fees apply.
Find out more about the Kindle Personal Document Service.
To save this article to your Dropbox account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you used this feature, you will be asked to authorise Cambridge Core to connect with your Dropbox account. Find out more about saving content to Dropbox.
To save this article to your Google Drive account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you used this feature, you will be asked to authorise Cambridge Core to connect with your Google Drive account. Find out more about saving content to Google Drive.