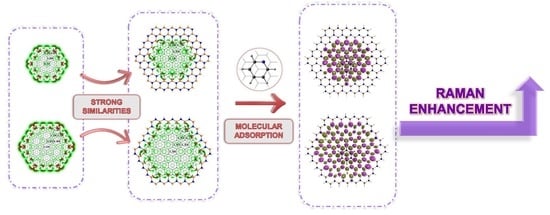
Potential Application of h-BNC Structures in SERS and SEHRS Spectroscopies: A Theoretical Perspective
Abstract
:1. Introduction
2. Methodology
3. Results and Discussion
3.1. Electronic Properties of h-BNCs vs Isolated Graphene Nanodisks
3.2. Stability of Pyridine Adsorbed on Embedded Nanographenes
3.3. Resonances in Pyridine+h-BNC Complexes
3.4. Enhancement of (Non)Linear Response Properties in Pyridine+h-BNC Complexes
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ling, X.; Xie, L.; Fang, Y.; Xu, H.; Zhang, H.; Kong, J.; Dresselhaus, M.S.; Zhang, J.; Liu, Z. Can Graphene be used as a Substrate for Raman Enhancement? Nano Lett. 2010, 10, 553–561. [Google Scholar] [CrossRef]
- Xu, W.; Mao, N.; Zhang, J. Graphene: A Platform for Surface-Enhanced Raman Spectroscopy. Small 2013, 9, 1206–1224. [Google Scholar] [CrossRef] [PubMed]
- Ling, X.; Huang, S.; Deng, S.; Mao, N.; Kong, J.; Dresselhaus, M.S.; Zhang, J. Lighting Up the Raman Signal of Molecules in the Vicinity of Graphene Related Materials. Acc. Chem. Res. 2015, 48, 1862–1870. [Google Scholar] [CrossRef] [PubMed]
- Kang, L.; Chu, J.; Zhao, H.; Xu, P.; Sun, M. Recent progress in the applications of graphene in surface-enhanced Raman scattering and plasmon-induced catalytic reactions. J. Mater. Chem. 2015, 3, 9024–9037. [Google Scholar] [CrossRef]
- Chelibanova, V.P.; Ktitorovb, S.A.; Polubotkob, A.M.; Firsovb, Y.A. SERS Mechanism on Graphene. arXiv 2017, arXiv:1607.06932. [Google Scholar]
- Ling, X.; Moura, L.G.; Pimenta, M.A.; Zhang, J. Charge-Transfer Mechanism in Graphene-Enhanced Raman Scattering. J. Phys. Chem. C 2012, 116, 25112–25118. [Google Scholar] [CrossRef]
- Ling, X.; Wu, J.; Xie, L.; Zhang, J. Graphene-Thickness-Dependent Graphene-Enhanced Raman Scattering. J. Phys. Chem. C 2013, 117, 2369–2376. [Google Scholar] [CrossRef]
- Joo, Y.; Kim, M.; Kanimozhi, C.; Huang, P.; Wong, B.M.; Roy, S.S.; Arnold, M.S.; Gopalan, P. Effect of Dipolar Molecule Structure on the Mechanism of Graphene Enhanced Raman Scattering. J. Phys. Chem. C 2016, 120, 13815–13824. [Google Scholar] [CrossRef]
- Ling, X.; Fang, W.; Lee, Y.-H.; Araujo, P.T.; Zhang, X.; Rodriguez-Nieva, J.F.; Lin, Y.; Zhang, J.; Kong, J.; Dresselhaus, M.S. Raman Enhancement Effect on Two-Dimensional Layered Materials: Graphene, h-BN and MoS2. Nano Lett. 2014, 14, 3033–3040. [Google Scholar] [CrossRef] [PubMed]
- Fesenko, O.; Dovbeshko, G.; Dementjev, A.; Karpicz, R.; Kaplas, T.; Svirko, Y. Graphene-enhanced Raman spectroscopy of thymine adsorbed on single-layer graphene. Nanoscale Res. Lett. 2015, 10, 163. [Google Scholar] [CrossRef]
- Barros, E.B.; Dresselhaus, M.S. Theory of Raman enhancement by two-dimensional materials: Applications for graphene-enhanced Raman spectroscopy. Phys. Rev. B 2014, 90, 035443. [Google Scholar] [CrossRef]
- Ling, X.; Zhang, J. First-Layer Effect in Graphene-Enhanced Raman Scattering. Small 2010, 6, 2020–2025. [Google Scholar] [CrossRef]
- Xu, H.; Chen, Y.; Xu, W.; Zhang, H.; Kong, J.; Dresselhaus, M.S.; Zhang, J. Modulating the Charge-Transfer Enhancement in GERS using an Electrical Field under Vacuum and an n/p-Doping Atmosphere. Small 2011, 7, 2945–2952. [Google Scholar] [CrossRef]
- Rana, F. Graphene Terahertz Plasmon Oscillators. IEEE Trans. Nanotech. 2008, 7, 91–99. [Google Scholar] [CrossRef] [Green Version]
- Nie, S.M.; Emory, S.R. Probing Single Molecules and Single Nanoparticles by Surface-Enhanced Raman Scattering. Science 1997, 275, 1102–1106. [Google Scholar] [CrossRef] [PubMed]
- Xie, L.; Ling, X.; Fang, Y.; Zhang, J.; Liu, Z. Graphene as a substrate to suppress fluorescence in Resonance Raman Spectroscopy. J. Am. Chem. Soc. 2009, 131, 9890–9891. [Google Scholar] [CrossRef] [PubMed]
- Xu, W.; Ling, X.; Xiao, J.; Dresselhaus, M.S.; Kong, J.; Xu, H.; Liu, Z.; Zhang, J. Surface enhanced Raman spectroscopy on a flat graphene surface. PNAS 2012, 109, 9281–9286. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Huang, S.; Ling, X.; Liang, L.; Song, Y.; Fang, W.; Zhang, J.; Kong, J.; Meunier, V.; Dresselhaus, M.S. Molecular Selectivity of Graphene-Enhanced Raman Scattering. Nano Lett. 2015, 15, 2892–2901. [Google Scholar] [CrossRef] [PubMed]
- Huang, S.; Pandey, R.; Barman, I.; Kong, J.; Dresselhaus, M. Raman Enhancement of Blood Constituent Proteins Using Graphene. ACS Photonics 2018, 5, 2978–2982. [Google Scholar] [CrossRef]
- Ding, S.Y.; Yi, J.; Li, J.F.; Ren, B.; Wu, D.Y.; Panneerselvam, R.; Tian, Z.Q. Nanostructure-based plasmon-enhanced Raman spectroscopy for surface analysis of materials. Nat. Rev. Mater. 2016, 1, 16021. [Google Scholar] [CrossRef]
- Feng, S.; dos Santos, M.C.; Carvalho, B.R.; Lv, R.; Li, Q.; Fujisawa, K.; Elías, A.L.; Lei, Y.; Perea-López, N.; Endo, M.; et al. Ultrasensitive molecular sensor using N-doped graphene through enhanced Raman scattering. Sci. Adv. 2016, 2, e1600322. [Google Scholar] [CrossRef]
- Grigorenko, A.N.; Polini, M.; Novoselov, K.S. Graphene Plasmonics. Nat. Photonics 2012, 6, 749–758. [Google Scholar] [CrossRef]
- Lv1, R.; Li, Q.; Botello-Méndez, A.R.; Hayashi, T.; Wang, B.; Berkdemir, A.; Hao, Q.; Elías, A.L.; Cruz-Silva, R.; Gutiérrez, H.R.; et al. Nitrogen-doped graphene: Beyond single substitution and enhanced molecular sensing. Sci. Rep. 2012, 2, 586. [Google Scholar]
- Thongrattanasiri, S.; Manjavacas, A.; García de Abajo, F.J. Quantum finite-size effects in graphene plasmons. ACS Nano 2012, 6, 1766–1775. [Google Scholar] [CrossRef] [PubMed]
- Manjavacas, A.; Marchesin, F.; Thongrattanasiri, S.; Koval, P.; Nordlander, P.; Sánchez-Portal, D.; García de Abajo, F.J. Tunable molecular plasmons in polycyclic aromatic hydrocarbons. ACS Nano 2013, 7, 3635–3643. [Google Scholar] [CrossRef] [PubMed]
- Ramos-Berdullas, N.; López-Carballeira, D.; Pérez-Juste, I.; Mandado, M. On the mechanism responsible of Raman enhancement on carbon allotropes surfaces: The role of molecule-surface vibrational coupling in SERS. J. Raman. Spectrosc. 2015, 46, 1205–1214. [Google Scholar] [CrossRef]
- López-Carballeira, D.; Ramos-Berdullas, N.; Pérez-Juste, I.; Mandado, M. Can single graphene nanodisks be used as Raman enhancement platforms? RSC Adv. 2016, 6, 71397–71403. [Google Scholar] [CrossRef]
- Kong, X.; Chen, Q.; Li, R.; Cheng, K.; Yan, N.; Chen, J.; Zhou, Y. Theoretical Investigation on SERS of Pyridine Adsorbed on Cn Clusters Induced by Charge Transfer: A Hint that SERS Could be Applied on Many Materials. ChemPhysChem 2012, 13, 1449–1453. [Google Scholar] [CrossRef] [PubMed]
- Konga, X.-K.; Chenb, Q.-W.; Suna, Z.-Y. Enhanced SERS of the complex substrate using Au supported on graphene with pyridine and R6G as the probe molecules. Chem. Phys. Lett. 2013, 564, 54–59. [Google Scholar] [CrossRef]
- Karamanis, P.; Otero, N.; Pouchan, C. Electric property variations in nanosized hexagonal boron nitride/graphene hybrids. J. Phys. Chem. C 2015, 119, 11872–11885. [Google Scholar] [CrossRef]
- Otero, N.; El-Kelany, K.E.; Pouchan, C.; Rérat, M.; Karamanis, P. Establishing the pivotal role of local aromaticity in the electronic properties of boron-nitride graphene lateral hybrids. Phys. Chem. Chem. Phys. 2016, 18, 25315–25328. [Google Scholar] [CrossRef] [PubMed]
- Karamanis, P.; Otero, N.; Pouchan, C. Unleashing the quadratic nonlinear optical responses of graphene by confining white-graphene (h-BN) sections in its framework. J. Am. Chem. Soc. 2014, 113, 7464–7473. [Google Scholar] [CrossRef] [PubMed]
- Otero, N.; Karamanis, P.; El-Kelany, K.E.; Rérat, M.; Maschio, L.; Civalleri, B.; Kirtman, B. Exploring the linear optical properties of borazine (B3N3) doped graphenes. 0D flakes vs 2D sheets. J. Phys. Chem. C 2017, 121, 709–722. [Google Scholar] [CrossRef]
- Otero, N.; Pouchan, C.; Karamanis, P. Quadratic nonlinear optical (NLO) properties of borazino (B3N3)-doped nanographenes. J. Phys. Chem. C 2017, 5, 8273–8287. [Google Scholar] [CrossRef]
- Ci, L.; Song, L.; Jin, C.; Jariwala, D.; Wu, D.; Li, Y.; Srivastava, A.; Wang, Z.F.; Storr, K.; Balicas, L.; et al. Atomic layers of hybridized boron nitride and graphene domains. Nat. Mater. 2010, 10, 430–435. [Google Scholar] [CrossRef]
- Gong, Y.; Shi, G.; Zhang, Z.; Zhou, W.; Jung, J.; Gao, W.; Ma, L.; Yang, Y.; Yang, S.; You, G.; et al. Direct chemical conversion of graphene to boron- and nitrogen- and carbon-containing atomic layers. Nat. Commun. 2014, 5, 3193. [Google Scholar] [CrossRef] [Green Version]
- Lorenzo-García, M.M.; Bonifazi, D. Renaissance of an Old Topic: From Borazines to BN-doped Nanographenes. Chimia 2017, 71, 550–557. [Google Scholar] [CrossRef] [PubMed]
- Ramos-Berdullas, N.; Pérez-Juste, I.; Van Alsenoy, C.; Mandado, M. Theoretical study of the adsorption of aromatic units on carbon allotropes including explicit (empirical) DFT dispersion corrections and implicitly dispersion-corrected functionals: The pyridine case. Phys. Chem. Chem. Phys. 2015, 17, 575–587. [Google Scholar] [CrossRef]
- Boys, S.F.; Bernardi, F. The calculation of small molecular interactions by the differences of separate total energies. Some procedures with reduced errors. Mol. Phys. 1970, 19, 553–566. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09, Revision E.01; Gaussian, Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Mandado, M.; Hermida-Ramón, J.M. Electron Density Based Partitioning Scheme of Interaction Energies. J. Chem. Theory Comput. 2011, 7, 633–641. [Google Scholar] [CrossRef]
- Chemcraft - Graphical Software for Visualization of Quantum Chemistry Computations. Available online: https://www.chemcraftprog.com (accessed on 20 April 2019).
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [PubMed]
- Krishtal, A.; Senet, P.; Yang, M.; Van Alsenoy, C. A Hirshfeld partitioning of polarizabilities of water clusters. J. Chem. Phys. 2006, 125, 034312. [Google Scholar] [CrossRef] [PubMed]
- Otero, N.; Van Alsenoy, C.; Pouchan, C.; Karamanis, P. Hirshfeld-Based Intrinsic Polarizability Density Representations as a Tool to Analyze Molecular Polarizability. J. Comput. Chem. 2015, 36, 1831–1843. [Google Scholar] [CrossRef]
- Giambiagi, M.; De Giambiagi, M.S.; Mundim, K.C. Definition of a multicenter bond index. Struct. Chem. 1990, 1, 423–427. [Google Scholar] [CrossRef]
- Sannigrahi, A.B.; Kar, T. Three-center bond index. Chem. Phys. Lett. 1990, 173, 569–572. [Google Scholar] [CrossRef]
- Ponec, R.; Uhlik, F. Multicentre Bond Indices from the Generalized Population Analysis of Higher Order Densities. Croat. Chem. Acta 1996, 69, 941–954. [Google Scholar]
- Bultinck, P.; Ponec, R.; Van Damme, S. Multicenter bond indices as a new measure of aromaticity in polycyclic aromatic hydrocarbons. J. Phys. Org. Chem. 2005, 18, 706–718. [Google Scholar] [CrossRef]
- Mandado, M.; González-Moa, M.J.; Mosquera, R.A. QTAIM N-Center Delocalization Indices as Descriptors of Aromaticity in Mono and Poly Heterocycles. J. Comput. Chem. 2007, 28, 127–136. [Google Scholar] [CrossRef]
- Bultinck, P.; Van Alsenoy, C.; Ayers, P.W.; Carbó-Dorca, R. Critical analysis and extension of the Hirshfeld atoms in molecules. J. Chem. Phys. 2007, 126, 144111. [Google Scholar] [CrossRef] [Green Version]





| Isolated | Embedded | Isolated/Embedded | |
|---|---|---|---|
| C6BN | 18.43 | 6.80 | 2.71 |
| C24BN | 38.12 | 27.72 | 1.38 |
| C54BN | 75.61 | 55.86 | 1.35 |
| C54BN2 | 75.61 | 61.82 | 1.22 |
| C96BN | 124.68 | 104.06 | 1.20 |
| C24BN | dX | dY | dZ | OS | EW | C54BN | dX | dY | dZ | OS | EW |
| 1 | 0.00 | −0.01 | 0.00 | 0.00 | 2.133 | 1 | 0.00 | 0.00 | 0.00 | 0.00 | 1.400 |
| 2 | 4.22 | −0.17 | −0.02 | 1.07 | 2.456 | 2 | −5.45 | 0.00 | 0.03 | 1.38 | 1.893 |
| 3 | −0.17 | −4.22 | 0.00 | 1.08 | 2.471 | 3 | 0.00 | 5.44 | 0.00 | 1.38 | 1.900 |
| 4 | −0.11 | 0.00 | −0.06 | 0.00 | 2.683 | 4 | −0.03 | 0.00 | 0.00 | 0.00 | 2.298 |
| 5 | −0.02 | 0.00 | 0.01 | 0.00 | 2.735 | 5 | 0.00 | 0.04 | 0.00 | 0.00 | 2.344 |
| 6 | −0.08 | −1.24 | 0.00 | 0.10 | 2.774 | 6 | 0.05 | 0.00 | −0.01 | 0.00 | 2.452 |
| 7 | 1.24 | −0.07 | 0.00 | 0.11 | 2.775 | 7 | 0.00 | 1.42 | 0.00 | 0.12 | 2.472 |
| 8 | −0.04 | −0.96 | 0.00 | 0.07 | 2.858 | 8 | 1.37 | 0.00 | −0.01 | 0.11 | 2.478 |
| 9 | 1.20 | −0.05 | −0.01 | 0.10 | 2.872 | 9 | 0.00 | 1.99 | 0.00 | 0.24 | 2.503 |
| 10 | −0.16 | −2.64 | 0.00 | 0.50 | 2.935 | 10 | −2.14 | 0.00 | 0.01 | 0.28 | 2.510 |
| 11 | 2.57 | −0.16 | −0.01 | 0.48 | 2.937 | 11 | 0.00 | 0.47 | 0.00 | 0.01 | 2.513 |
| 12 | 0.01 | 0.11 | 0.00 | 0.00 | 2.944 | 12 | 0.01 | 0.00 | −0.01 | 0.00 | 2.626 |
| 13 | 0.00 | 0.00 | −0.23 | 0.00 | 2.971 | 13 | 0.00 | 0.05 | 0.00 | 0.00 | 2.634 |
| 14 | 0.00 | −0.03 | 0.00 | 0.00 | 3.072 | 14 | 0.00 | −0.33 | 0.00 | 0.01 | 2.677 |
| 15 | −0.17 | 0.01 | 0.00 | 0.00 | 3.082 | 15 | −0.37 | 0.00 | 0.00 | 0.01 | 2.683 |
| 16 | 0.06 | 0.00 | −0.03 | 0.00 | 3.137 | 16 | −0.04 | 0.00 | 0.00 | 0.00 | 2.692 |
| 17 | 0.00 | −0.09 | 0.00 | 0.00 | 3.140 | 17 | −0.36 | 0.00 | 0.00 | 0.01 | 2.847 |
| 18 | −0.01 | −0.45 | 0.00 | 0.02 | 3.210 | 18 | 0.00 | 0.28 | 0.00 | 0.01 | 2.848 |
| 19 | 0.42 | −0.01 | −0.01 | 0.01 | 3.213 | 19 | 2.46 | −0.01 | −0.01 | 0.44 | 2.966 |
| 20 | 0.00 | 0.01 | 0.00 | 0.00 | 3.266 | 20 | −0.01 | −2.54 | 0.00 | 0.47 | 2.966 |
| C54BN2 | dX | dY | dZ | OS | EW | C96BN | dX | dY | dZ | OS | EW |
| 1 | 0.00 | 0.02 | 0.00 | 0.00 | 2.423 | 1 | 0.00 | 0.00 | 0.00 | 0.00 | 1.947 |
| 2 | −0.04 | 0.00 | 0.01 | 0.00 | 2.498 | 2 | 0.06 | 0.00 | 0.00 | 0.00 | 2.002 |
| 3 | −5.15 | 0.00 | −0.02 | 1.94 | 2.986 | 3 | −6.06 | 0.00 | 0.03 | 2.21 | 2.454 |
| 4 | 0.00 | −5.16 | 0.00 | 1.95 | 2.989 | 4 | 0.00 | 6.08 | 0.00 | 2.22 | 2.456 |
| 5 | 0.00 | 0.00 | 0.00 | 0.00 | 3.306 | 5 | 0.00 | −0.13 | 0.00 | 0.00 | 2.678 |
| 6 | 0.00 | −0.45 | 0.00 | 0.02 | 3.340 | 6 | 0.05 | 0.00 | −0.01 | 0.00 | 2.697 |
| 7 | −0.49 | 0.00 | −0.06 | 0.02 | 3.342 | 7 | 0.00 | 0.11 | 0.00 | 0.00 | 2.697 |
| 8 | 0.00 | −0.30 | 0.00 | 0.01 | 3.470 | 8 | 0.00 | −0.28 | 0.00 | 0.01 | 2.815 |
| 9 | 0.42 | 0.00 | −0.05 | 0.02 | 3.471 | 9 | −0.42 | 0.00 | 0.00 | 0.01 | 2.818 |
| 10 | 0.11 | 0.00 | −0.03 | 0.00 | 3.691 | 10 | 0.00 | −0.22 | 0.00 | 0.00 | 2.983 |
| 11 | 0.00 | −0.17 | 0.00 | 0.00 | 3.698 | 11 | −0.12 | 0.00 | −0.01 | 0.00 | 3.025 |
| 12 | 0.00 | 0.18 | 0.00 | 0.00 | 3.800 | 12 | 0.00 | 0.20 | 0.00 | 0.00 | 3.092 |
| 13 | 0.17 | 0.00 | 0.09 | 0.00 | 3.808 | 13 | 0.32 | 0.00 | −0.01 | 0.01 | 3.094 |
| 14 | −0.47 | 0.00 | −0.06 | 0.02 | 3.947 | 14 | 0.00 | 0.88 | 0.00 | 0.06 | 3.191 |
| 15 | 0.00 | 0.52 | 0.00 | 0.03 | 3.953 | 15 | 0.80 | 0.00 | −0.01 | 0.05 | 3.193 |
| 16 | 0.02 | 0.00 | −0.05 | 0.00 | 3.987 | 16 | −0.10 | 0.00 | −0.03 | 0.00 | 3.253 |
| 17 | 0.03 | 0.00 | 0.01 | 0.00 | 4.027 | 17 | −2.20 | 0.00 | 0.01 | 0.39 | 3.317 |
| 18 | −1.37 | 0.00 | 0.00 | 0.19 | 4.036 | 18 | 0.00 | 2.16 | 0.00 | 0.38 | 3.319 |
| 19 | 0.00 | 1.38 | 0.00 | 0.19 | 4.038 | 19 | −0.02 | 0.00 | 0.01 | 0.00 | 3.408 |
| 20 | 0.00 | 0.14 | 0.00 | 0.00 | 4.081 | 20 | 0.00 | −0.17 | 0.00 | 0.00 | 3.455 |
| C24BN | αiso | βT |
|---|---|---|
| 532.0 nm a/0.0 nm | 2.24 | 268.05 |
| 505.0 nm b/0.0 nm | 160 | 6.8 × 107 |
| C54BN | ||
| 633.0 nm a/0.0 nm | 2.07 | 297.64 |
| 655.3 nm b/0.0 nm | 300 | 3.9 × 107 |
| C54BN2 | ||
| 458.0 nm a/0.0 nm | 1.93 | 43.80 |
| 415.4 nm b/0.0 nm | 180 | 0.9 × 107 |
| C96BN | ||
| 532.0 nm a/0.0 nm | 3.36 | 218.65 |
| 505.8 nm b/0.0 nm | 280 | 2.1 × 107 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gil-Guerrero, S.; Otero, N.; Queizán, M.; Mandado Alonso, M. Potential Application of h-BNC Structures in SERS and SEHRS Spectroscopies: A Theoretical Perspective. Sensors 2019, 19, 1896. https://doi.org/10.3390/s19081896
Gil-Guerrero S, Otero N, Queizán M, Mandado Alonso M. Potential Application of h-BNC Structures in SERS and SEHRS Spectroscopies: A Theoretical Perspective. Sensors. 2019; 19(8):1896. https://doi.org/10.3390/s19081896
Chicago/Turabian StyleGil-Guerrero, Sara, Nicolás Otero, Marta Queizán, and Marcos Mandado Alonso. 2019. "Potential Application of h-BNC Structures in SERS and SEHRS Spectroscopies: A Theoretical Perspective" Sensors 19, no. 8: 1896. https://doi.org/10.3390/s19081896
APA StyleGil-Guerrero, S., Otero, N., Queizán, M., & Mandado Alonso, M. (2019). Potential Application of h-BNC Structures in SERS and SEHRS Spectroscopies: A Theoretical Perspective. Sensors, 19(8), 1896. https://doi.org/10.3390/s19081896