SEVIRI Hyper-Fast Forward Model with Application to Emissivity Retrieval
Abstract
:1. Introduction
2. Principal Component Analysis Approach to SEVIRI Radiative Transfer Modelling
2.1. Radiative Transfer Modelling
- is the surface emissivity
- is the total atmospheric transmittance
- is the Planck function computed at the surface temperature,
- is the atmospheric emission term
- is the down-welling thermal radiation reflected at the surface within the satellite viewing angle
2.2. Linear Regression and PCA Decomposition
2.3. Step by Step Description of -SEVIRI and Details on the Spectral Data Base to Compute the Monochromatic Predictors, , , and
3. Data
3.1. In Situ Data
3.2. IASI Data
4. Results
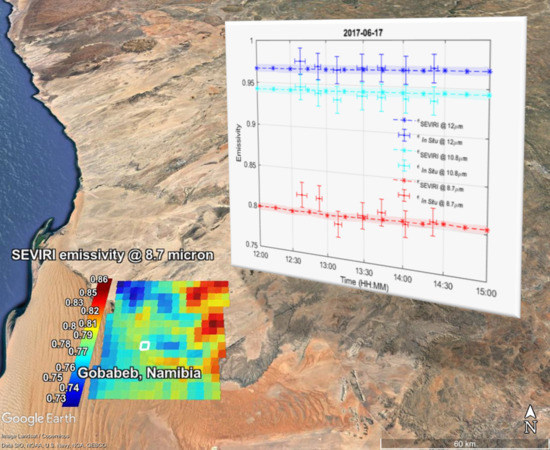
4.1. SEVIRI v/s In Situ
4.2. SEVIRI v/s IASI
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Abbreviations
| AVHRR | Advanced Very High Resolution Radiometer |
| ECMWF | European Centre for Medium Range Weather Forecasts |
| EUMETSAT | European Centre for the Exploitation of Meteorological Satellites |
| ESA | European Space Agency |
| IASI | Infrared Atmospheric Sounder Interferometer |
| LSA | Land Surface Analysis |
| MIUR | Italian Ministry of Education, University and Research |
| NPL | National Physical Laboratory |
| PCA | Principal Component Analysis |
| SAF | Satellite Applictaion Facility |
References
- Masiello, G.; Serio, C.; De Feis, I.; Amoroso, M.; Venafra, S.; Trigo, I.F.; Watts, P. Kalman filter physical retrieval of surface emissivity and temperature from geostationary infrared radiances. Atmos. Meas. Tech. 2013, 6, 3613–3634. [Google Scholar] [CrossRef] [Green Version]
- Masiello, G.; Serio, C.; Venafra, S.; Liuzzi, G.; Göttsche, F.-M.; Trigo, I.F.; Watts, P. Kalman filter physical retrieval of surface emissivity and temperature from SEVIRI infrared channels: A validation and intercomparison study. Atmos. Meas. Tech. 2015, 8, 2981–2997. [Google Scholar] [CrossRef]
- Blasi, M.G.; Liuzzi, G.; Masiello, G.; Serio, C.; Telesca, V.; Venafra, S. Surface parameters from SEVIRI observations through a kalman filter approach: Application and evaluation of the scheme to the southern Italy. Tethys 2016, 13, 3–10. [Google Scholar] [CrossRef]
- Kalman, R.E. A new approach to linear filtering and prediction problems. J. Basic Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef]
- Kalman, R.E.; Bucy, R.S. New Results in Linear Filtering and Prediction Theory. J. Basic Eng. 1961, 83, 95–108. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Li, Z.; Jin, X.; Schmit, T.J.; Zhou, L.; Goldberg, M.D. Land surface emissivity from high temporal resolution geostationary infrared imager radiances: 1. Methodology and simulation studies. J. Geophys. Res. 2011, 116, D01304. [Google Scholar] [CrossRef]
- Li, Z.; Li, J.; Li, Y.; Zhang, Y.; Schmit, T.J.; Zhou, L.; Goldberg, M.D.; Menzel, W.P. Determining diurnal variations of land surface emissivity from geostationary satellites. J. Geophys. Res. 2012, 117, D23302. [Google Scholar] [CrossRef]
- Li, Z.-L.; Tang, B.-H.; Wu, H.; Ren, H.; Yan, G.; Wan, Z.; Trigo, I.F.; Sobrino, J.A. Satellite-derived land surface temperature: Current status and perspectives. Remote Sens. Environ. 2013, 131, 14–37. [Google Scholar] [CrossRef] [Green Version]
- Dash, P.; Göttsche, F.-M.; Olesen, F.-S.; Fischer, H. Land surface temperature and emissivity estimation from passive sensor data: Theory and practice–current trends. Int. J. Remote Sens. 2002, 23, 2563–2594. [Google Scholar] [CrossRef]
- Gillespie, A.; Shuichi Rokugawa, S.; Matsunaga, T.; Cothern, J.S.; Hook, S.; Kahle, A.B. A temperature and emissivity separation algorithm for Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) images. IEEE Trans. Geosci. Remote 1998, 36, 1113–1126. [Google Scholar] [CrossRef]
- Li, J.; Li, J.; Weisz, E.; Zhou, D. Physical retrieval of surface emissivity spectrum from hyperspectral infrared radiances. Geophys. Res. Lett. 2007, 34, L16812. [Google Scholar] [CrossRef]
- Hulley, G.C.; Hook, S.J. Generating Consistent Land Surface Temperature and Emissivity Products Between ASTER and MODIS Data for Earth Science Research. IEEE Trans. Geosci. Remote 2011, 49, 1304–1315. [Google Scholar] [CrossRef]
- Masiello, G.; Serio, C. Simultaneous physical retrieval of surface emissivity spectrum and atmospheric parameters from infrared atmospheric sounder interferometer spectral radiances. Appl. Opt. 2013, 52, 2428–2446. [Google Scholar] [CrossRef] [PubMed]
- Masiello, G.; Serio, C.; Venafra, S.; De Feis, I.; Borbas, E.E. Diurnal variation in Sahara desert sand emissivity during the dry season from IASI observations. J. Geophys. Res. 2014, 119, 1626–1638. [Google Scholar] [CrossRef] [Green Version]
- Rozenstein, O.; Agam, N.; Serio, C.; Masiello, G.; Venafra, S.; Achal, S.; Puckrin, E.; Karnieli, A. Diurnal emissivity dynamics in bare versus biocrusted sand dunes. Sci. Total Environ. 2015, 506–507, 422–429. [Google Scholar] [CrossRef]
- Masiello, G.; Serio, C.; Venafra, S.; Liuzzi, G.; Poutier, L.; Göttsche, F.-M. Physical Retrieval of Land Surface Emissivity Spectra from Hyper-Spectral Infrared Observations and Validation with In Situ Measurements. Remote Sens. 2018, 10, 976. [Google Scholar] [CrossRef]
- Serio, C.; Amoroso, M.; Masiello, G.; Venafra, S.; Calbet, X.; Stuhlmann, R.; Tjemkes, S.; Watts, P. Expected profiling retrieval performance of the METEOSAT Third Generation Infrared Sounder. In Proceedings of the 9th International Symposium on Tropospheric Profiling, L’Aquila, Italy, 3–7 September 2012; ESA: Noordwijk, The Netherlands, 2012. ISBN 9789081583947. [Google Scholar]
- Berk, A.; Conforti, P.; Kennett, R.; Perkins, T.; Hawes, F.; van den Bosch, J. MODTRAN6: A major upgrade of the MODTRAN radiative transfer code. Proc. SPIE 2014, 9088. [Google Scholar] [CrossRef]
- Liuzzi, G.; Masiello, G.; Serio, C.; Blasi, M.G.; Venafra, S. Hyper fast radiative transfer for the physical retrieval of surface parameters from SEVIRI observations. J. Phys. Conf. Ser. 2012, 633, 012059. [Google Scholar] [CrossRef]
- Venafra, S.; Blasi, M.G.; Liuzzi, G.; Masiello, G.; Serio, C. The Very First Multi-Temporal and Multi-Spectral Level-2 SEVIRI Processor for the Simultaneous Physical Retrieval of Surface Temperature and Emissivity. In Radiation Processes in the Atmosphere and Ocean (IRS 2016): Proceedings of the International Radiation Symposium (IRC/IAMAS), Auckland, New Zealand, 17–21 April 2016; American Institute of Physics: Melville, NY, USA, 2017; Volume 1810, p. 060005. [Google Scholar] [CrossRef]
- Göttsche, F.-M.; Olesen, F.-S.; Bork-Unkelbach, A. Validation of land surface temperature derived from MSG/SEVIRI with in situ measurements at Gobabeb, Namibia. Int. J. Remote Sens. 2013, 34, 3069–3083. [Google Scholar] [CrossRef]
- Göttsche, F.-M.; Olesen, F.-S.; Trigo, I.F.; Bork-Unkelbach, A.; Martin, M.A. Long Term Validation of Land Surface Temperature Retrieved from MSG/SEVIRI with Continuous in-Situ Measurements in Africa. Remote Sens. 2016, 8, 410. [Google Scholar] [CrossRef]
- Amato, U.; Masiello, G.; Serio, C.; Viggiano, M. The σ-IASI code for the calculation of infrared atmospheric radiance and its derivatives. Environ. Model. Softw. 2002, 17, 651–667. [Google Scholar] [CrossRef]
- Esposito, F.; Grieco, G.; Masiello, G.; Pavese, G.; Restieri, R.; Serio, C.; Cuomo, V. Intercomparison of line-parameter spectroscopic databases using downwelling spectral radiance. Q. J. R. Meteorol. Soc. 2007, 133, 191–202. [Google Scholar] [CrossRef] [Green Version]
- Grieco, G.; Masiello, G.; Serio, C. Interferometric vs Spectral IASI Radiances: Effective Data-Reduction Approaches for the Satellite Sounding of Atmospheric Thermodynamical Parameters. Remote Sens. 2010, 2, 2323–2346. [Google Scholar] [CrossRef] [Green Version]
- Liuzzi, G.; Masiello, G.; Serio, C.; Meloni, D.; Di Biagio, C.; Formenti, P. Consistency of dimensional distributions and refractive indices of desert dust measured over Lampedusa with IASI radiances. Atmos. Meas. Tech. 2017, 10, 599–615. [Google Scholar] [CrossRef] [Green Version]
- Becker, F.; Li, Z.-L. Surface temperature and emissivity at various scales: Definition, measurement and related problems. Remote Sens. Rev. 1995, 12, 225–253. [Google Scholar] [CrossRef]
- Knuteson, R.O.; Best, F.A.; DeSlover, D.H.; Osborne, B.J.; Revercomb, H.E.; Smith, W.L., Sr. Infrared land surface remote sensing using high spectral resolution aircraft observations. Adv. Space Res. 2004, 33, 1114–1119. [Google Scholar] [CrossRef]
- Guillevic, P.; Göttsche, F.; Nickeson, J.; Hulley, G.; Ghent, D.; Yu, Y.; Trigo, I.; Hook, S.; Sobrino, J.A.; Remedios, J.; et al. Land Surface Temperature Product Validation Best Practice Protocol. In Best Practice for Satellite-Derived Land Product Validation; version 1.0; Guillevic, P., Göttsche, F., Nickeson, J., Roman, M., Eds.; Land Product Validation Subgroup (WGCV/CEOS): Greenbelt, MD, USA, January 2018; p. 58. [Google Scholar] [CrossRef]
- Chevallier, F. Sampled Database of 60 Levels of Atmospheric Profiles from the ECMWF Analysis; ECMWF EUMETSAT SAF Programme Research Report 4; ECMWF: Reading, UK, 2002; Available online: https://www.ecmwf.int/en/elibrary/8684-sampled-database-60-level-atmospheric-profiles-ecmwf-analyses (accessed on 1 March 2019).
- Anderson, G.P.; Clough, S.A.; Kneizys, F.X.; Chetwynd, J.H.; Shettle, E.P. Atmospheric Constituent Profiles (0–120 Km); Geophysics Laboratory: Hanscom Air Force Base, MA, USA, 1986. [Google Scholar]
- Masiello, G.; Serio, C. An effective water vapor self-broadening scheme for look-up-table-based radiative transfer. In Remote Sensing of Clouds and the Atmosphere VII; Schäfer, K.P., Lado-Bordowsky, O., Comerón, A., Picard, R.H., Eds.; SPIE: Bellingham, WA, USA, April 2003; Volume 4882, pp. 52–61. [Google Scholar]
- Göttsche, F.-M.; Olesen, F.; Poutier, L.; Langlois, S.; Wimmer, W.; Garcia Santos, V.; Coll, C.; Niclos, R.; Arbelo, M.; Monchau, J.P. Fiducial Reference Measurements for Validation of Surface Temperature From Satellites (FRM4STS); Report from the Field Inter-Comparison Experiment (FICE) for Land Surface Temperature; Karlsruhe Institute of Technology (KIT): Eggenstein-Leopoldshafen, Germany, 2017. [Google Scholar]
- Hilton, F.; Armante, R.; August, T.; Barnet, C.; Bouchard, A.; Camy-Peyret, C.; Capelle, V.; Clarisse, L.; Clerbaux, C.; Coheur, P.; et al. Hyperspectral Earth Observation from IASI: Five Years of Accomplishments. Bull. Am. Meteorol. Soc. 2012, 93, 347–370. [Google Scholar] [CrossRef] [Green Version]










| Channel # | Wave Length Center (m) | Wave Number Center (cm) | Radiometric Noise (NEDT, K) |
|---|---|---|---|
| 4 | 3.9 | 2564 | 0.35 at 300 K |
| 5 | 6.2 | 1613 | 0.75 at 250 K |
| 6 | 7.3 | 1370 | 0.75 at 250 K |
| 7 | 8.7 | 1148 | 0.28 at 300 K |
| 8 | 9.7 | 1035 | 1.5 at 255 K |
| 9 | 10.8 | 929 | 0.25 at 300 K |
| 10 | 12.0 | 838 | 0.37 at 300 K |
| 11 | 13.4 | 746 | 1.80 at 270 K |
| Channel (m) | r | % | (cm) | (W/m (cm) sr K) | ||
|---|---|---|---|---|---|---|
| 12 | 30 | 6 | 99.95 | 838 | 0.99799 | 1.03182 × 10 |
| 10.8 | 20 | 5 | 99.94 | 929 | 0.99376 | 6.56584 × 10 |
| 8.7 | 30 | 9 | 99.95 | 1148 | 1.00304 | −2.55525 × 10 |
| Total | 80 | 20 |
| Layer | Pressure (hPa) | Layer | Pressure (hPa) | Layer | Pressure (hPa) | Layer | Pressure (hPa) |
|---|---|---|---|---|---|---|---|
| 1 | 1050.0–975.0 | 8 | 650.0–550.0 | 15 | 125.0–85.0 | 22 | 6.0–4.0 |
| 2 | 975.0–937.5 | 9 | 550.0–450.0 | 16 | 85.0–60.0 | 23 | 4.0–2.5 |
| 3 | 937.5–912.5 | 10 | 450.0–350.0 | 17 | 60.0–40.0 | 24 | 2.5–1.5 |
| 4 | 912.5–875.0 | 11 | 350.0–275.0 | 18 | 40.0–25.0 | 25 | 1.5–0.5 |
| 5 | 875.0–825.0 | 12 | 275.0–225.0 | 19 | 25.0–15.0 | ||
| 6 | 825.0–750.0 | 13 | 225.0–175.0 | 20 | 15.0–8.5 | ||
| 7 | 750.0–650.0 | 14 | 175.0–125.0 | 21 | 8.5–6.0 |
| Date | Letter | Area | Number of Aggregated Measurements | Comments |
|---|---|---|---|---|
| 17 June 2017 | A | Mast | 7 | seven spots around the fence, shared with Themacs |
| two measurements per spot | ||||
| 22 June 2017 | B | Mast 2 | 1 | 15 measurements along a 20-m line, four on disturbed soil |
| measurements (the gravel is covered by sand/dust) | ||||
| 23 June 2017 | C | GRTC | 1 | 16 measurements, three sets of samples; 30 m between sets, |
| each set covering a 5-m line | ||||
| 24 June 2017 | D | Road | 1 | ten measurements along a 30-m line at the starting |
| point of the road experiment |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Masiello, G.; Serio, C.; Venafra, S.; Poutier, L.; Göttsche, F.-M. SEVIRI Hyper-Fast Forward Model with Application to Emissivity Retrieval. Sensors 2019, 19, 1532. https://doi.org/10.3390/s19071532
Masiello G, Serio C, Venafra S, Poutier L, Göttsche F-M. SEVIRI Hyper-Fast Forward Model with Application to Emissivity Retrieval. Sensors. 2019; 19(7):1532. https://doi.org/10.3390/s19071532
Chicago/Turabian StyleMasiello, Guido, Carmine Serio, Sara Venafra, Laurent Poutier, and Frank-M. Göttsche. 2019. "SEVIRI Hyper-Fast Forward Model with Application to Emissivity Retrieval" Sensors 19, no. 7: 1532. https://doi.org/10.3390/s19071532
APA StyleMasiello, G., Serio, C., Venafra, S., Poutier, L., & Göttsche, F.-M. (2019). SEVIRI Hyper-Fast Forward Model with Application to Emissivity Retrieval. Sensors, 19(7), 1532. https://doi.org/10.3390/s19071532