Improving the Triple-Carrier Ambiguity Resolution with a New Ionosphere-Free and Variance-Restricted Method
Abstract
:1. Introduction
2. Methodology
2.1. EWL Ambiguity Resolution
2.2. WL Ambiguity Resolution
2.3. NL Ambiguity Resolution
3. Results
3.1. Experiments Setup
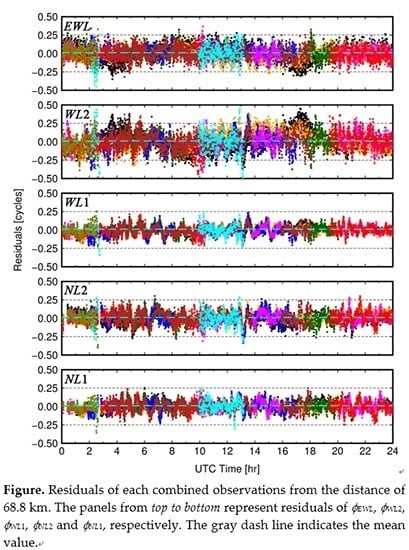
3.2. Error Analysis of the Combined Observation
3.3. Performance of Ambiguity Resolution
4. Concluding Remarks
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Procedure for Selecting the Code Combined Coefficients
Appendix B. Proof of Equivalence of IFVR and GBUC Method
References
- Teunissen, P.J. The least-squares ambiguity decorrelation adjustment: A method for fast GPS integer ambiguity estimation. J. Geodesy 1995, 70, 65–82. [Google Scholar] [CrossRef]
- Forssell’, B.; Martin-Neira, M.; Harrisz, R. Carrier phase ambiguity resolution in GNSS-2. In Proceedings of the 10th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GPS 1997), Kansas City, MO, USA, 16–19 September 1997; pp. 1727–1736. [Google Scholar]
- Vollath, U.; Birnbach, S.; Landau, L.; Fraile-Ordoñez, J.M.; Martí-Neira, M. Analysis of Three-Carrier Ambiguity Resolution Technique for Precise Relative Positioning in GNSS-2. Navigation 1999, 46, 13–23. [Google Scholar] [CrossRef]
- Feng, Y. GNSS three carrier ambiguity resolution using ionosphere-reduced virtual signals. J. Geodesy 2008, 82, 847–862. [Google Scholar] [CrossRef]
- Henkel, P.; Günther, C. Reliable Integer Ambiguity Resolution: Multi-Frequency Code Carrier Linear Combinations and Statistical A Priori Knowledge of Attitude. Navigation 2012, 59, 61–75. [Google Scholar] [CrossRef]
- Li, B.; Feng, Y.; Gao, W.; Li, Z. Real-time kinematic positioning over long baselines using triple-frequency BeiDou signals. IEEE Trans. Aerosp. Electron. Syst. 2015, 51, 3254–3269. [Google Scholar] [CrossRef]
- Chen, D.; Ye, S.; Xia, J.; Liu, Y.; Xia, P. A geometry-free and ionosphere-free multipath mitigation method for BDS three-frequency ambiguity resolution. J. Geodesy 2016, 90, 703–714. [Google Scholar] [CrossRef]
- Cocard, M.; Bourgon, S.; Kamali, O.; Collins, P. A systematic investigation of optimal carrier-phase combinations for modernized triple-frequency GPS. J. Geodesy 2008, 82, 555–564. [Google Scholar] [CrossRef]
- Tang, W.; Deng, C.; Shi, C.; Liu, J. Triple-frequency carrier ambiguity resolution for Beidou navigation satellite system. GPS Solut. 2014, 18, 335–344. [Google Scholar] [CrossRef]
- Li, B.; Verhagen, S.; Teunissen, P.J. Robustness of GNSS integer ambiguity resolution in the presence of atmospheric biases. GPS Solut. 2014, 18, 283–296. [Google Scholar] [CrossRef]
- Sieradzki, R.; Paziewski, J. Study on reliable GNSS positioning with intense TEC fluctuations at high latitudes. GPS Solut. 2016, 20, 553–563. [Google Scholar] [CrossRef]
- Sieradzki, R.; Paziewski, J. MSTIDs impact on GNSS observations and its mitigation in rapid static positioning at medium baselines. Ann. Geophys. 2016, 58, 0661. [Google Scholar]
- Wang, K.; Rothacher, M. Ambiguity resolution for triple-frequency geometry-free and ionosphere-free combination tested with real data. J. Geodesy 2013, 87, 539–553. [Google Scholar] [CrossRef]
- Li, J.; Yang, Y.; He, H.; Guo, H. An analytical study on the carrier-phase linear combinations for triple-frequency GNSS. J. Geodesy 2017, 91, 151–166. [Google Scholar] [CrossRef]
- Odijk, D. Ionosphere-free phase combinations for modernized GPS. J. Surv. Eng. 2003, 129, 165–173. [Google Scholar] [CrossRef]
- Richert, T.; El-Sheimy, N. Optimal linear combinations of triple frequency carrier phase data from future global navigation satellite systems. GPS Solut. 2007, 11, 11–19. [Google Scholar] [CrossRef]
- Li, B.; Feng, Y.; Shen, Y. Three carrier ambiguity resolution: Distance-independent performance demonstrated using semi-generated triple frequency GPS signals. GPS Solut. 2010, 14, 177–184. [Google Scholar] [CrossRef]
- Teunissen, P. On the sensitivity of the location, size and shape of the GPS ambiguity search space to certain changes in the stochastic model. J. Geodesy 1997, 71, 541–551. [Google Scholar] [CrossRef]
- Geng, J.; Bock, Y. Triple-frequency GPS precise point positioning with rapid ambiguity resolution. J. Geodesy 2013, 87, 449–460. [Google Scholar] [CrossRef]
- Zhao, Q.; Dai, Z.; Hu, Z.; Sun, B.; Shi, C.; Liu, J. Three-carrier ambiguity resolution using the modified TCAR method. GPS Solut. 2015, 19, 589–599. [Google Scholar] [CrossRef]
- Li, L.; Jia, C.; Zhao, L.; Yang, F.; Li, Z. Integrity monitoring-based ambiguity validation for triple-carrier ambiguity resolution. GPS Solut. 2017, 21, 797–810. [Google Scholar] [CrossRef]
- Liu, L.; Wan, W.; Ning, B.; Pirog, O.; Kurkin, V. Solar activity variations of the ionospheric peak electron density. J. Geophys. Res. Space Phys. 2006, 111. [Google Scholar] [CrossRef]
- Misra, P.; Enge, P. Global Positioning System: Signals, Measurements and Performance, 2nd ed.; Ganga-Jamuna Press: Lincoln, MA, USA, 2006. [Google Scholar]
- Urquhart, L. An Analysis of Multi-Frequency Carrier Phase Linear Combinations for GNSS; Technical Report No. 263; Universtiy of New Brunswick: Fredericton, NB, Canada, 2009. [Google Scholar]
- Joosten, P.; Teunissen, P.J.; Jonkman, N. GNSS three carrier phase ambiguity resolution using the LAMBDA-method. Proc. GNSS 1999, 99, 5–8. [Google Scholar]
- Saastamoinen, J. Contributions to the theory of atmospheric refraction. Bull. Géodésique (1946–1975) 1973, 107, 13–34. [Google Scholar] [CrossRef]
- Niell, A. Global mapping functions for the atmosphere delay at radio wavelengths. J. Geophys. Res. Solid Earth 1996, 101, 3227–3246. [Google Scholar] [CrossRef]
- Wielgosz, P.; Paziewski, J.; Baryła, R. On constraining zenith tropospheric delays in processing of local GPS networks with Bernese software. Surv. Rev. 2011, 43, 472–483. [Google Scholar] [CrossRef]
- Ding, F.; Wan, W.; Xu, G.; Yu, T.; Yang, G.; Wang, J.S. Climatology of medium-scale traveling ionospheric disturbances observed by a GPS network in central China. J. Geophys. Res. Space Phys. 2011, 116. [Google Scholar] [CrossRef]
- Zhang, X.; He, X. Performance analysis of triple-frequency ambiguity resolution with BeiDou observations. GPS Solut. 2016, 20, 269–281. [Google Scholar] [CrossRef]
- Li, L.; Li, Z.; Yuan, H.; Wang, L.; Hou, Y. Integrity monitoring-based ratio test for GNSS integer ambiguity validation. GPS Solut. 2016, 20, 573–585. [Google Scholar] [CrossRef]
- Montenbruck, O.; Hauschild, A.; Steigenberger, P.; Hugentobler, U.; Teunissen, P.; Nakamura, S. Initial assessment of the COMPASS/BeiDou-2 regional navigation satellite system. GPS Solut. 2013, 17, 211–222. [Google Scholar] [CrossRef]
- Schaffrin, B.; Grafarend, E. Generating classes of equivalent linear models by nuisance parameter elimination. Manuscr. Geod. 1986, 11, 262–271. [Google Scholar]
- Shen, Y.; Xu, G. Simplified equivalent representation of GPS observation equations. GPS Solut. 2008, 12, 99–108. [Google Scholar] [CrossRef]
- Li, B.; Ge, H.; Shen, Y. Comparison of Ionosphere-free, Uofc and Uncombined PPP Observation Models. Acta Geod. Cartogr. Sin. 2015, 44, 734–740. [Google Scholar]





| Observations | Combination |
|---|---|
| φEWL | |
| φWL1 | |
| φWL2 | |
| φNL1 | |
| φNL2 |
| No. | Dis. | UTC | Duration | Interval(s) |
|---|---|---|---|---|
| 1 | 7.7 km | 2013/3/20 | 24 h | 30 |
| 2 | 22.4 km | 2015/10/27 | 24 h | 30 |
| 3 | 42.5 km | 2014/2/26 | 24 h | 30 |
| 4 | 68.8 km | 2014/2/26 | 24 h | 30 |
| Dis. | φNL1 | φNL2 | φWL1 | φWL2 | φEWL |
|---|---|---|---|---|---|
| 7.7 km | 0.05 | 0.06 | 0.03 | 0.10 | 0.09 |
| 22.4 km | 0.06 | 0.08 | 0.04 | 0.13 | 0.10 |
| 42.5 km | 0.06 | 0.07 | 0.05 | 0.14 | 0.10 |
| 68.8 km | 0.06 | 0.07 | 0.06 | 0.12 | 0.09 |
| Amb. | Dis. | GBIR | GFIF | IFVR | |||
|---|---|---|---|---|---|---|---|
| Pfix | Pcf | Pfix | Pcf | Pfix | Pcf | ||
| EWL | 7.7 km | 100 | 100 | 100 | 100 | 100 | 100 |
| 22.4 km | 100 | 100 | 100 | 100 | 100 | 100 | |
| 42.5 km | 100 | 100 | 100 | 100 | 100 | 100 | |
| 68.8 km | 100 | 100 | 100 | 100 | 100 | 100 | |
| WL | 7.7 km | 100 | 100 | 100 | 100 | 100 | 100 |
| 22.4 km | 100 | 100 | 100 | 100 | 100 | 100 | |
| 42.5 km | 100 | 100 | 100 | 100 | 100 | 100 | |
| 68.8 km | 100 | 100 | 100 | 100 | 100 | 100 | |
| NL | 7.7 km | 99.1 | 99.9 | 96.6 | 99.9 | 97.6 | 99.9 |
| 22.4 km | 98.5 | 100 | 98.1 | 100 | 98.4 | 100 | |
| 42.5 km | 66.1 | 98.0 | 98.3 | 100 | 99.5 | 100 | |
| 68.8 km | 22.5 | 30.5 | 86.4 | 100 | 92.1 | 100 | |
| Dis. | GBIR | GFIF | IFVR | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| STD | SEP (95%) | STD | SEP (95%) | STD | SEP (95%) | |||||||
| E | N | U | E | N | U | E | N | U | ||||
| 7.7 km | 0.2 | 0.3 | 2.3 | 9.3 | 0.7 | 0.5 | 1.8 | 8.2 | 0.7 | 1.1 | 2.3 | 7.6 |
| 22.4 km | 0.2 | 0.4 | 0.7 | 5.4 | 0.2 | 0.2 | 1.3 | 4.8 | 0.1 | 0.1 | 2 | 6.4 |
| 42.5 km | 0.7 | 0.9 | 3.5 | 7.0 | 0.5 | 0.4 | 3.2 | 6.6 | 0.5 | 0.4 | 3.3 | 6.5 |
| 68.8 km | 5.9 | 3.4 | 6.2 | 20.8 | 0.5 | 0.3 | 2.3 | 11.1 | 0.8 | 0.5 | 3.6 | 12.9 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, C.; Zhao, L.; Li, L.; Li, H.; Cheng, J.; Li, Z. Improving the Triple-Carrier Ambiguity Resolution with a New Ionosphere-Free and Variance-Restricted Method. Remote Sens. 2017, 9, 1108. https://doi.org/10.3390/rs9111108
Jia C, Zhao L, Li L, Li H, Cheng J, Li Z. Improving the Triple-Carrier Ambiguity Resolution with a New Ionosphere-Free and Variance-Restricted Method. Remote Sensing. 2017; 9(11):1108. https://doi.org/10.3390/rs9111108
Chicago/Turabian StyleJia, Chun, Lin Zhao, Liang Li, Hui Li, Jianhua Cheng, and Zishen Li. 2017. "Improving the Triple-Carrier Ambiguity Resolution with a New Ionosphere-Free and Variance-Restricted Method" Remote Sensing 9, no. 11: 1108. https://doi.org/10.3390/rs9111108
APA StyleJia, C., Zhao, L., Li, L., Li, H., Cheng, J., & Li, Z. (2017). Improving the Triple-Carrier Ambiguity Resolution with a New Ionosphere-Free and Variance-Restricted Method. Remote Sensing, 9(11), 1108. https://doi.org/10.3390/rs9111108