Global Surface Mass Variations from Continuous GPS Observations and Satellite Altimetry Data
Abstract
:1. Introduction
2. Theory and Methodology
2.1. Elastic Deformation
2.2. GPS Observations
2.3. Ocean Bottom Pressure and Satellite Altimetry
2.4. Adjustment Model by Combining GNSS and Satellite Altimetry
2.4.1. Observation Equations
2.4.2. A Priori Constraint
2.4.3. Adjustment Model
3. Results and Discussion
3.1. Time-Varying Gravity Field Estimates
3.2. Global Surface Mass Redistribution
3.2.1. Estimation of Equivalent Water Thickness
3.2.2. Variations in Terrestrial Water Storage
3.2.3. Annual Water Cycle in Amazon
3.2.4. Estimation of Mass Error
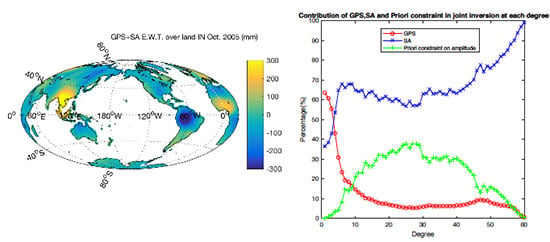
3.3. Sensitivity Analysis
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
References
- Tapley, B.D.; Bettadpur, S.; Watkins, M.; Reigber, C. GRACE measurements of mass variability in the Earth system. Science 2004, 305, 503–505. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.L.; Wilson, C.R.; Tapley, B.D. Satellite gravity measurements confirm accelerated melting of Greenland ice sheet. Science 2006, 313, 1958–1960. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.L.; Wilson, C.R.; Tapley, B.D.; Famiglietti, J.S.; Rodell, M. Seasonal global mean sea level change from satellite altimeter, GRACE, and geophysical models. J. Geod. 2005, 79, 532–539. [Google Scholar] [CrossRef]
- Chen, J.L.; Rodell, M.; Wilson, C.R.; Famiglietti, J.S. Low degree spherical harmonic influences on Gravity Recovery and Climate Experiment (GRACE) water storage estimates. Geophys. Res. Lett. 2005. [Google Scholar] [CrossRef]
- Chen, J.L.; Wilson, C.R.; Tapley, B.D. Interannual variability of low-degree gravitational change, 1980–2002. J. Geod. 2005, 78, 535–543. [Google Scholar] [CrossRef]
- Chen, J.L.; Wilson, C.R.; Tapley, B.D.; Yang, Z.L.; Niu, G.Y. 2005 drought event in the Amazon River basin as measured by GRACE and estimated by climate models. J. Geophys. Res. Solid Earth 2009. [Google Scholar] [CrossRef]
- Chen, J.L.; Wilson, C.R.; Tapley, B.D. The 2009 exceptional Amazon flood and interannual terrestrial water storage change observed by GRACE. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Cheng, M.; Tapley, B.D. Variations in the Earth’s oblateness during the past 28 years. J. Geophys. Res. Solid Earth 2004. [Google Scholar] [CrossRef]
- Cheng, M.K.; Ries, J.C.; Tapley, B.D. Geocenter variations from analysis of SLR data. In Reference Frames for Applications in Geosciences; Springer: Berlin/Heidelberg, Germany, 2013; pp. 19–25. [Google Scholar]
- Cheng, M.; Ries, J.C.; Tapley, B.D. Variations of the Earth’s figure axis from satellite laser ranging and GRACE. J. Geophys. Res. Solid Earth 2011. [Google Scholar] [CrossRef]
- Cheng, M.; Tapley, B.D.; Ries, J.C. Deceleration in the Earth’s oblateness. J. Geophys. Res. 2013, 118, 740–747. [Google Scholar] [CrossRef]
- Sośnica, K.; Jäggi, A.; Meyer, U.; Thaller, D.; Beutler, G.; Arnold, D.; Dach, R. Time variable Earth’s gravity field from SLR satellites. J. Geod. 2015, 89, 945–960. [Google Scholar] [CrossRef] [Green Version]
- Kang, Z.; Tapley, B.; Chen, J.; Ries, J.; Bettadpur, S. Geocenter variations derived from GPS tracking of the GRACE satellites. J. Geod. 2009, 83, 895–901. [Google Scholar] [CrossRef]
- Lin, T.; Hwang, C.; Tseng, T.P.; Chao, B.F. Low-degree gravity change from GPS data of COSMIC and GRACE satellite missions. J. Geodyn. 2012, 53, 34–42. [Google Scholar] [CrossRef]
- Wang, X.; Gerlach, C.; Rummel, R. Time-variable gravity field from satellite constellations using the energy integral. Geophys. J. Int. 2012, 190, 1507–1525. [Google Scholar] [CrossRef]
- Rodell, M.; Velicogna, I.; Famiglietti, J.S. Satellite-based estimates of groundwater depletion in India. Nature 2009, 460, 999–1002. [Google Scholar] [CrossRef] [PubMed]
- Blewitt, G.; Lavallée, D.; Clarke, P.; Nurutdinov, K. A new global mode of Earth deformation: Seasonal cycle detected. Science 2001, 294, 2342–2345. [Google Scholar] [CrossRef] [PubMed]
- Wu, X.; Argus, D.F.; Heflin, M.B.; Ivins, E.R.; Webb, F.H. Site distribution and aliasing effects in the inversion for load coefficients and geocenter motion from GPS data. Geophys. Res. Lett. 2002. [Google Scholar] [CrossRef]
- Lavallée, D.A.; Van Dam, T.; Blewitt, G.; Clarke, P.J. Geocenter motions from GPS: A unified observation model. J. Geophys. Res. Solid Earth 2006. [Google Scholar] [CrossRef]
- Kusche, J.E.J.O.; Schrama, E.J.O. Surface mass redistribution inversion from global GPS deformation and Gravity Recovery and Climate Experiment (GRACE) gravity data. J. Geophys. Res. Solid Earth 2005. [Google Scholar] [CrossRef]
- Rietbroek, R.; Brunnabend, S.E.; Dahle, C.; Kusche, J.; Flechtner, F.; Schröter, J.; Timmermann, R. Changes in total ocean mass derived from GRACE, GPS, and ocean modeling with weekly resolution. J. Geophys. Res. Oceans 2009. [Google Scholar] [CrossRef]
- Rietbroek, R.; Fritsche, M.; Dahle, C.; Brunnabend, S.E.; Behnisch, M.; Kusche, J.; Dietrich, R. Can GPS-Derived Surface Loading Bridge a GRACE Mission Gap? Surv. Geophys. 2014, 35, 1267–1283. [Google Scholar] [CrossRef]
- Siegismund, F.; Romanova, V.; Köhl, A.; Stammer, D. Ocean bottom pressure variations estimated from gravity, nonsteric sea surface height and hydrodynamic model simulations. J. Geophys. Res. Oceans 2011. [Google Scholar] [CrossRef]
- Wu, X.; Heflin, M.B.; Ivins, E.R.; Fukumori, I. Seasonal and interannual global surface mass variations from multisatellite geodetic data. J. Geophys. Res. Solid Earth 2006. [Google Scholar] [CrossRef]
- Wu, X.; Heflin, M.B.; Schotman, H.; Vermeersen, B.L.; Dong, D.; Gross, R.S.; Owen, S.E. Simultaneous estimation of global present-day water transport and glacial isostatic adjustment. Nat. Geosci. 2010, 3, 642–646. [Google Scholar] [CrossRef]
- Wahr, J.; Molenaar, M.; Bryan, F. Time variability of the Earth’s gravity field: Hydrological and oceanic effects and their possible detection using GRACE. J. Geophys. Res. Solid Earth 1998, 103, 30205–30229. [Google Scholar] [CrossRef]
- Blewitt, G. Self-consistency in reference frames, geocenter definition, and surface loading of the solid Earth. J. Geophys. Res. Solid Earth 2003. [Google Scholar] [CrossRef]
- Kedar, S.; Bock, Y.; Moore, A.W.; Squibb, M.B.; Liu, Z.; Hasse, J.; Fang, P. Solid Earth Science ESDR System. In Proceedings of the 2013 American Geophysical Union (AGU) Fall Meeting, San Francisco, CA, USA, 9–13 December 2013; Available online: http://adsabs.harvard.edu/abs/2013AGUFM.G23C..08K (accessed on 5 August 2017).
- Mao, A.; Harrison, C.G.; Dixon, T.H. Noise in GPS coordinate time series. J. Geophys. Res. Solid Earth 1999, 104, 2797–2816. [Google Scholar] [CrossRef]
- Zhang, J.; Bock, Y.; Johnson, H.; Fang, P.; Williams, S.; Genrich, J.; Wdowinski, S.; Behr, J. Southern California Permanent GPS Geodetic Array: Error analysis of daily position estimates and site velocities. J. Geophys. Res. Solid Earth 1997, 102, 18035–18055. [Google Scholar] [CrossRef]
- Jayne, S.R.; Wahr, J.M.; Bryan, F.O. Observing ocean heat content using satellite gravity and altimetry. J. Geophys. Res. Oceans 2003. [Google Scholar] [CrossRef]
- Leuliette, E.W.; Miller, L. Closing the sea level rise budget with altimetry, Argo, and GRACE. Geophys. Res. Lett. 2009. [Google Scholar] [CrossRef]
- Blewitt, G.; Clarke, P. Inversion of Earth’s changing shape to weigh sea level in static equilibrium with surface mass redistribution. J. Geophys. Res. Solid Earth 2003. [Google Scholar] [CrossRef]
- Bettadpur, S. Level-2 Gravity Field Product User Handbook. Available online: http://csrserv.csr.utexas.edu/grace/publications/handbook/L2-UserHandbook_v1.0.pdf (accessed on 5 August 2017).
- Ishii, M.; Kimoto, M. Reevaluation of historical ocean heat content variations with time-varying XBT and MBT depth bias corrections. J. Oceanogr. 2009, 65, 287–299. [Google Scholar] [CrossRef]
- Ishii, M.; Kimoto, M.; Sakamoto, K.; Iwasaki, S.I. Steric sea level changes estimated from historical ocean subsurface temperature and salinity analyses. J. Oceanogr. 2006, 62, 155–170. [Google Scholar] [CrossRef]
- Zheng, D.W.; Zhong, P.; Ding, X.L.; Chen, W. Filtering GPS time-series using a Vondrak filter and cross-validation. J. Geod. 2005, 79, 363–369. [Google Scholar] [CrossRef]
- Swenson, S.; Chambers, D.; Wahr, J. Estimating geocenter variations from a combination of GRACE and ocean model output. J. Geophys. Res. Solid Earth 2008. [Google Scholar] [CrossRef]
- Chambers, D.P. Converting Release-04 Gravity Coefficients into Maps of Equivalent Water Thickness; University of Texas at Austin: Austin, TX, USA, 2007. [Google Scholar]
- Wahr, J.; Swenson, S.; Velicogna, I. Accuracy of GRACE mass estimates. Geophys. Res. Lett. 2006. [Google Scholar] [CrossRef]
- Jansen, M.J.F.; Gunter, B.C.; Kusche, J. The impact of GRACE, GPS and OBP data on estimates of global mass redistribution. Geophys. J. Int. 2009, 177, 1–13. [Google Scholar] [CrossRef]
- Zhang, X.; Jin, S. Uncertainties and effects on geocenter motion estimates from global GPS observations. Adv. Space Res. 2014, 54, 59–71. [Google Scholar] [CrossRef]
- Jin, S.G.; Luo, O.F.; Gleason, S. Characterization of diurnal cycles in ZTD from a decade of global GPS observations. J. Geodesy 2009, 83, 537–545. [Google Scholar] [CrossRef]
- Jin, S.G.; Zhang, T.; Zou, F. Glacial density and GIA in Alaska estimated from ICESat, GPS and GRACE measurements. J. Geophys. Res. Earth Surf. 2017, 122, 76–90. [Google Scholar] [CrossRef]


















| GPS+SA | SLR | GRACE | |
|---|---|---|---|
| Annual Amplitudes (geocenter unit: mm) | |||
| X | 0.81 ± 0.14 | 4.37 ± 0.29 | 2.26 ± 0.12 |
| Y | 1.79 ± 0.15 | 2.26 ± 0.30 | 2.38 ± 0.09 |
| Z | 2.29 ± 0.19 | 4.54 ± 0.42 | 2.24 ± 0.16 |
| C20 | 1.05 ± 0.14 × 10−10 | 1.39 ± 0.08 × 10−10 | 1.50 ± 0.18 × 10−10 |
| C21 | 0.24 ± 0.09 × 10−10 | 0.23 ± 0.04 × 10−10 | 0.17 ± 0.03 × 10−10 |
| S21 | 0.98 ± 0.08 × 10−10 | 0.86 ± 0.05 × 10−10 | 0.79 ± 0.05 × 10−10 |
| C22 | 0.25 ± 0.08 × 10−10 | 0.13 ± 0.04 × 10−10 | 0.14 ± 0.04 × 10−10 |
| S22 | 0.68 ± 0.09 × 10−10 | 0.62 ± 0.05 × 10−10 | 0.72 ± 0.04 × 10−10 |
| Annual Phases (unit: angular degree) | |||
| X | 83.41 ± 9.80 | 35.12 ± 3.82 | 59.86 ± 3.16 |
| Y | −35.65 ± 4.78 | −23.54 ± 7.44 | −39.70 ± 2.15 |
| Z | 36.25 ± 4.88 | 39.74 ± 5.24 | 69.13 ± 4.26 |
| C20 | 65.44 ± 7.73 | 52.43 ± 3.13 | 38.53 ± 6.85 |
| C21 | −144 ± 22.64 | −1.38 ± 9.69 | −47.60 ± 11.57 |
| S21 | −9.54 ± 4.87 | −14.21 ± 3.47 | −18.19 ± 3.51 |
| C22 | −157.24 ± 17.35 | −120.66 ± 17.88 | −157.91 ± 14.25 |
| S22 | −46.42 ± 7.76 | −49.29 ± 4.28 | −38.01 ± 3.19 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Jin, S.; Lu, X. Global Surface Mass Variations from Continuous GPS Observations and Satellite Altimetry Data. Remote Sens. 2017, 9, 1000. https://doi.org/10.3390/rs9101000
Zhang X, Jin S, Lu X. Global Surface Mass Variations from Continuous GPS Observations and Satellite Altimetry Data. Remote Sensing. 2017; 9(10):1000. https://doi.org/10.3390/rs9101000
Chicago/Turabian StyleZhang, Xinggang, Shuanggen Jin, and Xiaochun Lu. 2017. "Global Surface Mass Variations from Continuous GPS Observations and Satellite Altimetry Data" Remote Sensing 9, no. 10: 1000. https://doi.org/10.3390/rs9101000
APA StyleZhang, X., Jin, S., & Lu, X. (2017). Global Surface Mass Variations from Continuous GPS Observations and Satellite Altimetry Data. Remote Sensing, 9(10), 1000. https://doi.org/10.3390/rs9101000