A Study of Landfast Ice with Sentinel-1 Repeat-Pass Interferometry over the Baltic Sea

Abstract

Mapping of fast ice displacement and investigating sea ice rheological behavior is a major open topic in coastal ice engineering and sea ice modeling. This study presents first results on Sentinel-1 repeat-pass space borne synthetic aperture radar interferometry (InSAR) in the Gulf of Bothnia over the fast ice areas. An InSAR pair acquired in February 2015 with a temporal baseline of 12 days has been studied here in detail. According to our results, the surface of landfast ice in the study area was stable enough to preserve coherence over the 12-day baseline, while previous InSAR studies over the fast ice used much shorter temporal baselines. The advantage of longer temporal baseline is in separating the fast ice from drift ice and detecting long term trends in deformation maps. The interferogram showed displacement of fast ice on the order of 40 cm in the study area. Parts of the displacements were attributed to forces caused by sea level tilt, currents, and thermal expansion, but the main factor of the displacement seemed to be due to compression of the drift ice driven by southwest winds with high speed. Further interferometric phase and the coherence measurements over the fast ice are needed in the future for understanding sea ice mechanism and establishing sustainability of the presented InSAR approach for monitoring dynamics of the landfast ice with Sentinel-1 data.

1. Introduction

Landfast sea ice is a type of sea ice that is formed and fastened to the coastline, islands, grounded ridges or any fixed objects in waters. Further offshore, the drift ice moving by winds and sea currents is found and forms an interactive outer boundary for the landfast ice. In the Baltic Sea, this boundary can reach the isobaths of 5–15 m depending on how cold the winter is [1]. The landfast ice zone grows laterally during the winter, and its decay begins from the shoreline in the spring. Most of the winter, the landfast ice forms a stable ice cover.

Annual ice season lasts 5–7 months in the Baltic Sea, from November to May. The landfast ice and its mechanics are of major concern in the archipelago areas, especially in the Bay of Bothnia, the northernmost basin. In extreme forcing conditions, the landfast ice may break and move horizontally, therefore scouring of the sea bottom, and loading of the coastline and man-made structures take place [1]. These events put coastal structures, beacons and on-ice traffic in danger, and compromise safety for working on the ice. After the start of the melting season in the spring, ice floes and ridges may drift easily, causing increased land-ice interaction and coastal erosion. However, the spring ice has lower strength than the colder ice in the winter. Analytic tools [2,3] provide a first-order approach to examine the evolution of the landfast ice zone. These tools consist of simple models for ice formation, thickness, and breakage. With increasing thickness, the strength of the ice layer increases, and landfast ice boundary extends further out. The whole process is forced by air temperature, wind, and bathymetry. Physically based numerical models of the evolution of landfast ice zone do not yet exist.

While the mechanism of landfast ice breakage is generally understood, its details are not fully known. In addition, the lateral growth of landfast ice is more complex than a moving single boundary, and no suitable analytical or numerical models are available for describing the deterioration of landfast ice in the spring [1]. The lack of physically based models is partly attributed to historical reasons, as the landfast ice, unlike the drift ice, is less of an issue for winter navigation. To better understand, predict and monitor the landfast ice zone, more well-documented cases and analyses of the observations are needed. One widely used tool for mapping ice conditions is spaceborne radar. Radar methods have advantages in remote sensing of the sea ice due to relatively strong backscatter contrast between different ice types [4]. Therefore, spaceborne imaging radar is widely applied in ice condition monitoring [5]. SAR has been widely examined for the ice/open water classification [6,7]. Imaging radar, unlike optical instruments, has all-weather and day-and-night observation capability. In addition, imaging radars can provide better detail and spatial coverage compared to non-imaging radars [8]. Synthetic Aperture Radar (SAR) is a kind of imaging radar that employs advanced processing technology for achieving detailed images of underlying terrain and mapping its features. Furthermore, advanced SAR techniques such as the InSAR can be used for precise measurements of surface topography and displacements. Measurements of travel path variations as a function of the satellite position and time of acquisition allow generation of Digital Elevation Models (DEMs), and measurement of centimeter-scale surface displacements of the terrain [9] by differentiating the phase of two or more SAR images [10]. InSAR coherence and phase provide information of stability and changes in the underlying terrain with high accuracy.

As landfast ice is nearly stationary, it may experience small displacements in order to cm to meters [11]. These displacements can make cracks and fractures, which are dangerous for local people who use the ice cover for traveling, hunting and fishing, as well as for shipping communication. In addition, there are beacons that guide ships and dethatching landfast ice can move or destroy them. Having knowledge about these displacements in landfast ice zone can improve our understanding and modeling of landfast ice mechanics, and this progress is useful for making hazard coastal maps as well as improving sea ice models in freezing basins [11,12]. The landfast ice zone has been examined with different multi-parametric InSAR techniques in several prior studies, using X-, C- and L-bands [10,11,12]. European Remote Sensing satellite ERS-1 C-band SAR instrument was used in the northern Baltic Sea in 1998 to study the relation between InSAR coherence, SAR backscatter, phase changes and mechanical events [11]. L-band InSAR technique was employed to map landfast ice extent in the Alaskan coastal zone based on the Japanese Advanced Land Observing Satellite (ALOS) with a temporal baseline of 46 days. There, both interferometric phase pattern and coherence images were used to extract the landfast ice extent [12].

In a recent study in the Baltic Sea, X-band SAR of the Italian Cosmo-Sky Med constellation was used during the winter of 2012 [10], with a temporal baseline of one day. Shorter wavelengths (such as X-band) are in general more suitable for detection of small displacements of the fast ice. The InSAR coherence is a valuable remote sensing observable that can provide information about surface processes. There is a connection between coherence and backscattering images [10,11,13]. Berg et al. [10] assessed the relationship between coherence and backscattering in more advanced shape than in the prior study in 1998 [10,11]. They observed higher coherence along with high backscatter intensity at X-band [10], while an opposite trend was observed at C-band (studied regions were partly overlapping) [11]. Thus, the relationship between backscatter and coherence seemed to be case dependent with several possible explanations [10], although lack of field data complicated the interpretation.

With the launch of ESA (European Space Agency) Sentinel-1 satellite in 2014, a new unprecedented capability for C-band InSAR has emerged, as Sentinel-1 data are provided at no cost for users [14]. The Sentinel-1 SAR sensor is operating at four imaging modes (Extra Wide Swath (EW), Interferometric Wide (IW), Stripmap (SM), and Wave (WV)) and with different resolution from 5 to 400 m. In this study, we use IW mode of the C-band SAR radar aboard Sentinel-1 with 12-day temporal baseline to map landfast ice displacement. The IW mode acquires data with a 250-km swath at 5 m × 20 m spatial resolution, capturing three sub-swaths with Terrain Observation with Progressive Scans SAR (TOPSAR) technique [15].

This work is the first of its kind, in the examining of landfast ice properties and dynamics in the Baltic Sea with Sentinel-1. A crucial factor in the suitability of satellite sensor for sea ice monitoring is the temporal baseline. In two prior studies [10,11], the temporal baseline was one and three days, respectively. Applying a long baseline leads to a strong temporal decorrelation which lowers the ability to measure displacements, but on the other hand, it is useful for separating the fast ice from the drift ice and detecting long-term trends in sea ice displacements. In this work, we examine the potential of Sentinel-1 data, even with a temporal baseline of 12 days, to detect, monitor and quantify the landfast ice displacement under certain conditions.

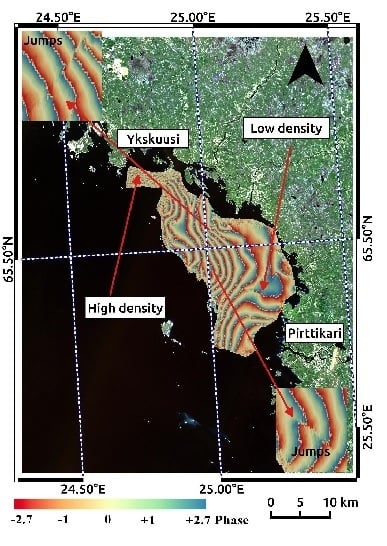
Furthermore, in this paper, we examine and provide the interpretation of an InSAR image pair acquired by Sentinel-1 over the northeast Bay of Bothnia in February 2015, with a temporal baseline of 12 days. In Section 2, we provide basic information about the InSAR in the context of ice-measurements, and in Section 3, study site, reference data and InSAR methodological approach in the study are described. Results are provided and discussed in Section 4. Results are presented by coherence and interferogram images and displacement map revealing a 40 cm displacement in the line of sight (LOS) direction. The study's conclusion, the potential for future research and application of the demonstrated technique are outlined in Section 5.

2. Fundamentals of InSAR Theory

The signal measured by SAR is essentially complex and can be represented in terms of real and imaginary parts or in terms of signal magnitude and phase. The phase of a single SAR image does not have any practical usage, but with two images acquired with slightly different viewing angles (interferometric pair), their phase difference after co-registration can be used to measure topography [16] and terrain displacement.

The coherence between two complex SAR images, s₁ and s₂, is the normalized complex cross-correlation between two complex signals (master and slave images). Coherent signals are used for interferometry [17]. The coherence$\gamma$ is formulated as [12,18]:

$$\gamma =\frac{\langle s_1{s}_2^{*}\rangle }{\sqrt{\langle s_1{s}_1^{*}\rangle \times \langle s_2{s}_2^{*}\rangle }}, 0\le \left|\gamma \right|\le 1,$$

(1)

where s₁ and s₂ are two complex SAR image values, and $\langle \dots \rangle$ denotes spatial averaging operation. The interferometric SAR coherence is also a complex value and can be represented in terms of the coherence magnitude and InSAR phase [18]. The coherence describes stability of the scattering process and therefore buildings and fixed land features have high levels of coherence, whereas changing and vegetated areas have low values of InSAR coherence. Open sea loses the InSAR coherence completely even within tens of milliseconds [10,19]. The landfast ice may exhibit both relatively high and low levels of coherence depending on the actual situation and parameters of InSAR measurement.

Several factors contribute to the magnitude of coherence:

$$\gamma ={\gamma }_{Thermal}\times {\gamma }_{Process}\times {\gamma }_{Spatial}\times {\gamma }_{Temporal},$$

(2)

where ${\gamma }_{Thermal}$ is related to the signal to noise ratio (SNR) of the system and caused by thermal noise in receiver; ${\gamma }_{Process}$ is processing decorrelation coming from errors in image interpolation, co-registration or spectral filtering; and ${\gamma }_{Spatial}$ is signal decorrelation due to the incidence angle differences, proportional to the perpendicular baseline B_⊥ which is dividing the two SAR antennas. As spatial coherence depends on baseline, it is called baseline decorrelation. The ${\gamma }_{Temporal}$ in the scattering space is the correlation factor for incoherent changes between satellite acquisitions. It is the most variable contributor while other decortication factors are almost stable. This component is the main factor for coherence losses. It can measure decorrelation due to ice movement or changes in scattered positions within a resolution cell [12].

Figure 1 shows how the phase difference between the two SAR images measured by the InSAR technique. The phase of each of the master and slave images shows random appearance. A phase interferogram is created by subtracting the phase of the “slave” from that of the “master” image. These phase differences become useful when a high coherence image is achieved. Equations (3)–(5) show how these phase differences $\Delta \phi$ are calculated:

$${\phi }_1=\frac{4\pi R}{\lambda },$$

(3)

$${\phi }_2=\frac{4\pi \times \left(R+\Delta R\right)}{\lambda },$$

(4)

$$\Delta \phi ={\phi }_2-{\phi }_1=\frac{4\pi \Delta R}{\lambda },$$

(5)

where ${\phi }_{1,2}$ is the phases of each of master and slave images, $\lambda$ is the satellite wavelength, and $R$ is satellite to target distance.

The phase difference can be represented as a combination of six sources. Equation (6) shows their contribution to SAR interferometric phase:

$$\Delta \phi ={\Phi }_{flat-earth}+\frac{4\mathsf{\pi }{B}_T}{\lambda Rsin\left(\theta \right)}\times \Delta h+\frac{4\pi }{\lambda }\Delta \eta +{\Phi }_{path,\mathrm{Atm}}+{\Phi }_{noise}+\mathrm{mod}\left(2\pi \right),$$

(6)

where $\theta$ is the incidence angle,$B_T$ is perpendicular baseline, $\Delta h$represents the topographic height, and $\Delta \eta$ represents the relative scatterer displacement projected on the slant range direction [11]. Other variables are defined in Equations (3)–(5).

Terms of Equation (6) are further explained here. The flat earth phase (${\Phi }_{flat-earth}$) is the phase contribution due to the Earth curvature. After interferogram flattening, the interferometric phase includes both altitude and displacement contributions. Topography phase ($\frac{4\pi B_T}{\lambda Rsin\left(\theta \right)}\times \Delta h$) is the topographic or altitude contribution to the interferometric phase that is used to determine elevation. If an accurate DEM is available, $\Phi$ topography can be computed and subtracted from the interferometric phase. This term is less relevant in this study. The displacement phase ($\frac{4\pi }{\lambda }\Delta \eta$) is the surface deformation or displacement contribution which we want to measure in this study. The fourth source is atmospheric phase (${\Phi }_{path,\mathrm{Atm}}$). Atmospheric condition changes between acquisitions. The radiation travel path for each of SAR images is affected differently by the atmosphere. These effects are produced by the atmospheric humidity, temperature and pressure change between the two acquisitions. It is hypothesized that a stable scatterer is present in each resolution cell but, in reality, it is different and many scatterers are present in each resolution cell that may change between acquisitions. Three main contributions to the phase noise (${\Phi }_{noise}$) are temporal change of the scatterers, phase noise due to different look angle and phase noise due to volume scattering. The last term of Equation (6) reflects the fact that the calculated phase is wrapped (has interferometric fringes) as the InSAR phase (or its difference) varies between 0 and 2π. The correct integer multiple of 2π to the InSAR phase is added during phase unwrapping [9,20].

Single-pass and repeat-pass interferometry are two major types of the InSAR methodology [20]. Note that the factor $\Delta \eta$ disappears in single-pass InSAR systems, so displacement measurement is impossible by these systems while both topography and small displacements measurements are possible with a repeat-pass system. The sensitivity of InSAR technique to the surface topography depends on satellite baseline in a repeat-pass system while the sensitivity to surface movements does not. Single-pass systems are useful for creating a topographic map while repeat-pass systems with a small baseline are preferable for making displacement maps [11,20].

3. Materials and Methods

3.1. Study Site, Reference Data, and InSAR Methodological Approach

In this study, two Sentinel-1 IW Single Look Complex (SLC) products from 6 and 18 February 2015 over the Bay of Bothnia were used. Landfast ice extent did not change between the two acquisitions, and the ice chart on 7 February represents the landfast ice condition in the period of the study (Figure 2). The SAR data consist of IW images on 6 and 18 February 2015, at 04:47:04 local time (EET) (Figure 3). IW swath mode has three sub-swaths, named IW1, IW2, and IW3. Our study area with high coherence is a part of IW2 sub-swath. It is located between Oulu and Kemi on the Finnish coast of the Bay of Bothnia. The normal (perpendicular) baseline is 51.21 m, and its incidence angle $\theta$ for IW2 is from 36.47° to 41.85° [21]. Sentinel-1 IW swath mode information is provided in

Table 1. Characteristics of Sentinel-1 interferometric mode [15].

Characteristic	Value
Swathwidth	250 km
Incidence Angle Range	29.1°–46.0°
Sub-Swaths	3, IW1, IW2, IW3
Azimuth Steering angle	±0.6°
Azimuth and Range looks	Single
Polarization Options	Dual HH + HV, VV + VH Single HH, VV
Maximum Noise Equivalent Sigma Zero (NESZ)	−22 dB
Radiometric Stability	0.5 dB (3σ)
Radiometric Accuracy	1 dB (3σ)
Phase Error	5°

.

The winter of 2015 was mild in the Baltic Sea. The peak of ice cover was on 23 January when the ice covered an area of 51,000 km². At this stage, the whole Bay of Bothnia was covered by the ice. Ice formation in the innermost bays of the northern Bay of Bothnia began in the middle of November. At the beginning of December, there was 1–10 cm thick level ice in the inner archipelago. Then, a cold spell began, lasting until 23 January, resulting in the maximum ice extent during this ice winter. There was another cold period around 5 February, and then the extent of ice reached 50,000 km². After this, the weather became milder, and southerly winds pushed the ice fields together toward the northeast. The rest of February was unusually mild. At the beginning of March, the ice extent was only 20,000 km². The maximum thickness of the landfast ice was 55 cm in the Bay of Bothnia. The thickness of drift ice was 15–40 cm [22].

The weather station at Kemi harbor, Ajos illustrates the conditions between acquisitions on 6 and 18 February 2015 over the Bay of Bothnia (Figure 4). The formation of permanent ice cover started on 24 December 2014, and the end of permanent ice cover was on 5 May 2015 [22].

3.2. InSAR Methodological Approach

In this study, the repeat-pass InSAR pair acquired by Sentinel-1 with a small perpendicular baseline is used to produce a displacement map. The Sentinel’s Application Platform (SNAP) software (version 5.0) was primarily used for processing the satellite SAR data, calculating coherence, and producing the interferogram. In addition, Quantum Geographic Information System (QGIS, 2.14.11-Essen version) software is another tool used in this research.

Interferogram processing chain starts with choosing two suitable SLC products in the study area. IW2 sub swath is selected based on our area of interest. Data products are available in VH and VV polarizations. Both polarizations are applied, although VV polarization is suitable for this research regarding high coherence magnitude level. By co-registering two SAR images (one master image and one slave image) into one stack, pixels in slave image move to align with pixels in the master image. In this step, we apply an orbit correction and use the DEM with back-geocoding co-registration. A schematic overview is shown in the co-registration block diagram (Figure 5). Next step is the interferogram formation and the coherence estimation. Interferometric phase and coherence are calculated in this step. Applying TOPSAR deburst removes demarcation area between every two bursts.

An optimal unwrapping result and increased fringe visibility (before unwrapping) are goals in any InSAR processing. Reaching these goals is possible by applying suitable multi-looking and additional phase-filtering of the interferogram. Goldstein phase filtering is applied for phase-filtering in this study. As there are some low coherence areas (such as sea and changed land surface), extracting a high coherence area is the best option for increasing the quality of unwrapped interferogram.

Statistical-cost Network-flow Algorithm for PHase Unwrapping (SNAPHU) is applied for phase unwrapping [19]. Further, the unwrapped phase is converted to a displacement map. Applying terrain correction, re-projection and re-sampling are final steps to obtain a geocoded product. Figure 6 shows our methodology steps.

4. Results and Discussion

According to reference data, the landfast ice thickness was 20–40 cm, and its extent was stable during the 12 days between the overflights. Landfast ice extended from Raahe on the eastern shores of the Bay of Bothnia to Kemi and Tornio in the north and then it continued on the Swedish side. The fast ice zone completely encircled Hailuoto Island of Oulu. Coherence magnitude is calculated based on Equation (1), interpretation of the interferogram over our area of interest is done using Equation (6), and they are analyzed with respect to the weather conditions during the image acquisitions.

4.1. Coherence Magnitude Analyses

The low coherence result destroys the unwrapped result (Figure 7b), which is why a high coherence area from the IW2 sub-swath is extracted by a polygon (Figure 7c). The mean coherence is relatively low over the low coherence area in VH polarization (Figure 8c) and VV polarization (Figure 8d), typically with values below 0.26.

The inner boundary of landfast ice zone or a high coherence area (Figure 7c) is located between Pirttikari and Ykskuusi with mean coherence value slightly higher than 0.3. This high coherence level gives us an acceptable unwrapped result. There are a few low coherence lines across the zone that are on-ice traffic routes between islands made and used by local people. It is interesting to see that coherence in the near-shore zone is lower. The outer boundary of the high coherence zone is sharp that reflects the location of the landfast ice edge (Figure 2).

The coherence level in this study may have decreased for several reasons. Firstly, there were two storm events, which may have caused mechanical ice displacements. Secondly, there were warm (air temperature is above 0 °C) periods, when minor melting in the surface layer and consequent melt-freeze metamorphosis may have taken place. Thirdly, there were cold periods that could have increased ice thickness by 5–10 cm in the study region [2]; however, no significant change was seen in Ajos ice station data [22]. Ice growth can lower coherence by increasing freeboard as implied by the Archimedes law. Fourthly, the low coherence can be caused by random movements of scatterers in snow and ice as well. Such movements can be caused by snow metamorphosis or dynamics of brine inclusions in sea ice.

Our observations showed that the accumulated sums of rain and snowfall were approximately 44 mm during the period between overflights, 38.8 mm solid and 5.2 mm in the liquid phase (Figure 4b, precipitation). The rainfall affected the surface characteristics and reduced coherence. If the weather is cold (air temperature is below 0 °C), snow on the ice is dry, and the interference with the radar is small [11]. In our case, several periods of melting might have reduced coherence (Figure 4a). If the surface layer becomes wet, then the backscatter suffers and will lose coherence. Melting–freezing cycles were other important causes of losing coherence. In addition, some factors contributed to high coherence over the polygon area. One of these factors was setting the polygon in the shallowest area in the Bay of Bothnia based on bathymetry information in the Baltic Sea [22]. Setting the polygon in the shallowest area increased the possibility of having grounding ridges. Islands serve as support points and so do grounded ridges, so these increase fast ice stability as well.

4.1.1. VH and VV Polarization Mode Comparison

The IW SLC acquisitions are in two VH and VV polarization modes. Both polarizations were studied over the area of interest. VV polarization coherence is much higher than VH polarization in interferometric coherence histograms (shown in Figure 8). It can be seen that VV coherence in the areas of landfast ice varies from 0.2 to 0.44, while VH coherence magnitude does not reach higher than 0.35. Thus, in the absence of any other structural differences between polarizations, our further analysis concentrated on the VV polarization mode.

4.2. Interferogram Analyses

Further, we examine the interferogram based on the Equation (6). As expected, the visibility of the interferometric phase fringes is limited by the high coherence polygon area (Figure 9a). Considering the form of the fringes, it is unlikely that they would have been produced by metamorphosis in the surface snow layer or ice growth. Rather, the background must be mechanical displacement.

The InSAR displacements are projections in LOS, i.e. the direction between the SAR antenna and the point on the ground. SAR imaging is performed not exactly below the satellite but on the side at a distance determined by the inclination angle (Figure 1). Ascending and descending orbits show observations from west and east respectively. The ground surface is changing in three dimensions. It includes east and west, north and south, up and down but an interferogram can show one-dimensional displacement, and it cannot determine whether the displacement is due to horizontal, vertical or combination of both. The Interferometric phase (Figure 9a) is converted to the displacement map shown in Figure 9b. This conversion includes the steps mentioned in Section 3.2. We applied multi-looking and phase-filtering after interferogram formation, then interferogram was unwrapped and, finally, converted to a displacement map. We chose an island as a grounded control point and calculated displacements based on it. In this case, both image acquisitions are made from the east (descending orbit). One fringe means almost 27.5 mm displacement in LOS. The measured LOS displacement is from –10 cm to 30 cm. Negative signs show the landfast ice is in the direction away from the satellite, which means that the landfast ice sinks or moves to the west. Positive signs show the landfast ice is in the direction close to the satellite, which means that landfast ice uplifts or moves to the east.

It is seen that the southern part of the high coherence polygon area in Figure 9b moves away while its northern part comes closer. Thus, there is a converging zone between southern and northern parts and the projected strain would be on the order of 40 cm across 20 km (Figure 9b). The 40 cm displacement could have been caused by viscous or plastic deformation during the 12 days.

One of the reasons for the vertical displacement can be sea level tilt. Absolute sea level cannot affect interferogram fringes because the landfast ice is afloat, but sea level tilting might affect fringes. Fringes can change by sea level differences according to ΔR = φ/2k, where φ is the interferometric phase, and $k=\frac{2\pi }{\lambda }$is the wave number, which is equal to 114.20 m⁻¹ here [10]. Two sea level stations, Kemi and Oulu, provided sea level data for our area (Figure 10). The plots are based on hourly data. In our period of study, the sea level dropped from 41.4 to 36.0 cm from 6 to 18 February in Oulu, and the corresponding change was from 39.7 to 36.5 cm in Kemi. Thus, the maximum relative change in sea level was 2.2 cm and the distance between sea level stations was 82 km. The absolute sea level ranged within ±50 cm in the period of study, but the whole water body moved up and down almost together leaving tilts across the basin below 5 cm over 100 km distance. These tilts can thus cause only minor relative vertical displacements in the landfast ice.

The vertical displacement due to ice growth and changes of freeboard must be less than 1 cm at the top, which is much smaller than what we measured. The lateral displacement could be due to thermal expansion. The linear thermal expansion coefficient is of the order of 10⁻⁴ °C⁻¹. However, the form of the fringes does not suggest thermal expansion has taken place. Precipitation is not expected to produce the observed gradients of changes over the study area.

We do not have water current measurements in the study area, but water currents beneath the landfast ice should be small. Winds are the principal reason of lateral displacements. The wind was from northwest compressing the drift ice on the land fast ice boundary had a minor influence on the inner part of the fast ice zone where the fringes are shown. There was simultaneous dilatation along the boundary, as typically takes place in such forcing conditions [23]. The physical realization of the small deformation was opening and closing of cracks. As seen in the SAR images in Figure 3, further out in the unstable outer part of fast ice boundary, heavier deformation with ridging has taken place. This area is away from the landfast ice boundary suggesting that the main load from the northwest storm has not reached our study area. Southwest winds with high speed, in order of 15 ms⁻¹ pushed the drift ice and put pressure on the landfast ice to northeast on 10, 16, and 17 February (Figure 4b, mean wind speed and wind direction). Movements were gradual over the landfast ice. There were some small jumps in the fringe pattern, which shows shearing and cracking (Jumps in Figure 9a). However, these cracks were not so strong for changing the fringe pattern and did not change fringe shape.

One research question is the low coherence and backscatter lines in the study area (black lines in Figure 3 and Figure 7). Some of them are recognizable as jumps in Figure 9a. These lines reach 600 meters in some areas. There are at least two possibilities to explain their presence: 1) They can be fractures due to landfast ice displacement, or 2) They can be routes on the ice. We overlaid one of the SAR backscatter images on the Google Earth map, and it was seen that the lines could be routes between islands that people use for fishing. Looking at Krassinletto Island (fishing island) shows that most of the black lines finished there. There are also some tracks that do not seem to reach an island, but that might be just because not all of the islands necessary appear on the Google Earth map or they can be some fishing camps on the ice. We have some areas with high fringe density demonstrating high displacement activity. The smoother transitions are more around islands especially if several islands locate near each other (Figure 9a) [11].

4.3. Comparison with Previous Works

To our knowledge, the InSAR techniques have been used at least twice before over the Baltic Sea to investigate the landfast ice mechanisms [10,11], but with very different set-up. In our study, the temporal baseline was the 12 days while, in two previous studies, the temporal baselines were much shorter, three days [11] and one day [10]. Two reasons for losing coherence in our study were increasing temperature and precipitation which were not seen in the previous studies. Air temperature reached over 0 °C several times during this study period while it was between −2.7 °C to −5 °C [11] and mainly between −16 °C and −1 °C in [10], although we can find one case in [10], where temperature increased from 0 °C to 5 °C and was the reason for losing much coherence. Dry snow cover retained coherence over the landfast ice in [11] while in our study snow cover may have experienced melting because of high temperature causing a loss of coherence.

Dammert et al. [11] examined three InSAR pairs. The first interferogram was formed in the winter of 1992 by the image pair 24 and 27 March, the second one by the image pair 27 and 30 March, and the third by 24 and 30 March. The largest displacement was seen over an ice patch that was cut by two icebreaker tracks; 94 cm compression towards north was detected. The ice patch was compressed mostly by the southeasterly wind and boundary forces of the drift ice floe south of the landfast ice edge. There was a small contribution also from the sea surface tilt. The icebreaker cuts were obvious from the change direction and form the fringes. In our case, we only had some small jumps in the fringe pattern which showed shearing and cracking. However, these cracks were not as strong as icebreaker fractures and did not change the fringe pattern.

Berg et al. [10] interpreted two interferograms from two image pairs, A (15 and 16 March 2012) and B (31 March and 1 April 2012). They evaluated the ice rheology image pair A and had a closer look at the compression in the center of the interferogram. There, fringes had high density. An ice patch was seen at the edge of the fast ice. A part of the drift ice moved towards the fast ice about 100 m in the one-day period between the overflights and then it was connected to the fast ice. By this connection, a pressure force was applied on the fast ice from the drift ice, although some forces may be applied by winds. The relative compression movement in LOS direction was three fringes over a distance of 1800 ± 25 m. Based on ice thickness and weather information, these fringes and compression could not produce only with wind and water currents. In addition, sea level tilt was small, approximately 5 mm, over the whole scene corresponded to a change in radar LOS of almost 4 mm, and thus compression should have been another source that was due to the force exerted by the impinging drift ice. In our case, with a particular 12-day period, there could be several kinds of forcing background for the fringes. Sea level tilt, currents, and thermal expansion played a small role here, but a likely realization was forcing by drift ices toward the landfast ice boundary by pushing the southwest winds. Damment et al. [11] showed that the fast ice compression could be described by viscous rheology used in sea ice modeling. This kind of rheology may also be the case in our study.

5. Conclusions

This study is the first one that uses Sentinel-1 synthetic aperture radar interferometry for studying the landfast ice mechanics with the long temporal baseline (12 days) over the Baltic Sea. One case from February 2015 is examined in detail. An area nearly 400 km² was found with well-defined fringes and total change in the LOS of 40 cm. A small part of displacements was possibly produced by sea level tilt, currents, and thermal expansion, but the main factor was compression of the drift ice driven by the southwest winds on the boundary of landfast ice.

To maintain a high coherence over the landfast ice, a short temporal baseline is needed. On the other hand, we need high coherence results by long temporal baseline for separating the fast ice from the drift ice. Detecting long-term trends in a fast ice displacement map is another advantage of long temporal baseline. In this study, for the first time, we detected these long-term trends on the Baltic fast ice. Lines with low coherence and backscattering were found over the fast ice that could fracture due to the landfast ice displacement or ice routes.

Small scale fast ice changes was probably affected by weather parameters and other phenomena such as snowfall and rainfall, changing air temperature, and ice growth/melting. This indicates that better ground truth data are needed for future studies of the InSAR over the fast ice.

Sentinel-1 satellite has some advantages compared to previous missions, including data accessibility and geographical coverage. Additional benefit is given by free software such as SNAP for easy data processing. Sentinel-1 uses TOPSAR mode. This technique has a uniform SNR and distributed target ambiguity ratio (DTAR) in comparison with other previous satellites. Previous missions used that Scans SAR mode for capturing data [15].

InSAR displacement maps can be used to gain more knowledge about the processes of fast ice development and deformation. This information is useful in making risk maps for cracking and the opening of leads, needed by the local communities. To better understand the fast ice mechanisms, interferograms from both ascending and descending orbits would be needed to solve two movement components [24]. Another exciting possibility is investigating six-day interferometric data using both Sentinel-1A and Sentinel-1B acquisitions to better understand the potential of Copernicus data in sea ice monitoring applications.