Automated Quantification of Surface Water Inundation in Wetlands Using Optical Satellite Imagery
Abstract
:1. Introduction
- Can the spatial properties of water bodies and inundated landscapes be accurately represented using sub-pixel water fractions derived from optical satellite images?
- Can the temporal inundation dynamics of inundated landscapes be accurately represented using sub-pixel water fractions derived from a time series of optical satellite images?
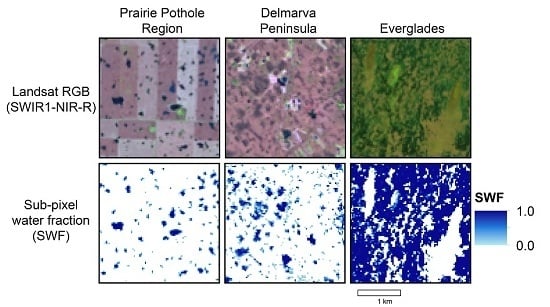
2. Site Descriptions
2.1. Canadian Prairie Pothole Region
2.2. Delmarva Peninsula
2.3. Florida Everglades
3. Methods
3.1. Satellite Data Acquisition and Pre-Processing
3.2. Dynamic Surface Water Extent (DSWE)
3.3. Quantifying Sub-Pixel Water Fraction (SWF)
3.4. Algorithm Assessment
3.4.1. Prairie Pothole Region
3.4.2. Delmarva Peninsula
3.4.3. Everglades
4. Results
4.1. Spatial Assessment
4.2. Temporal Assessment
5. Discussion
5.1. Automation and Scalability
5.2. Strengths and Limitations
5.2.1 Small Hemispherical Wetlands
5.2.2. Forested Depressional Wetlands
5.2.3. Large Heterogeneously Inundated Wetlands
5.3. Potential Applications of SWF
6. Conclusions
Acknowledgements
Author Contributions
Conflicts of Interest
References
- DeGroot, R.; Stuip, M.; Finlayson, M.; Davidson, N. Valuing Wetlands Guidance for Valuing the Benefits Derived from Wetland Ecosystem Services; Ramsar Convention Secretariat: Gland, Switzerland; Secretariat of the Convention on Biological Diversity: Montreal, QC, Canada, 2006. [Google Scholar]
- Clare, S.; Creed, I.F. Tracking wetland loss to improve evidence-based wetland policy learning and decision making. Wetl. Ecol. Manag. 2014, 22, 235–245. [Google Scholar] [CrossRef]
- Kingsford, R.T.; Basset, A.; Jackson, L. Wetlands: Conservation’s poor cousins. Aquat. Conserv. Mar. Freshw. Ecosyst. 2016, 26, 892–916. [Google Scholar] [CrossRef]
- Green, A.J.; Alcorlo, P.; Peeters, E.T.; Morris, E.P.; Espinar, J.L.; Bravo-Utrera, M.A.; Bustamante, J.; Díaz-Delgado, R.; Koelmans, A.A.; Mateo, R.; et al. Creating a safe operating space for wetlands in a changing climate. Front. Ecol. Environ. 2017, 15, 99–107. [Google Scholar] [CrossRef]
- Sass, G.Z.; Creed, I.F. Characterizing hydrodynamics on boreal landscapes using archived synthetic aperture radar imagery. Hydrol. Process. 2008, 22, 1687–1699. [Google Scholar] [CrossRef]
- Hayashi, M.; van der Kamp, G.; Rosenberry, D.O. Hydrology of Prairie Wetlands: Understanding the Integrated Surface-Water and Groundwater Processes. Wetlands 2016, 36, 237–254. [Google Scholar] [CrossRef]
- Creed, I.F.; Beall, F.D.; Clair, T.A.; Dillon, P.J.; Hesslein, R.H. Predicting export of dissolved organic carbon from forested catchments in glaciated landscapes with shallow soils. Glob. Biogeochem. Cycles 2008, 22. [Google Scholar] [CrossRef]
- Creed, I.F.; Beall, F.D. Distributed topographic indicators for predicting nitrogen export from headwater catchments. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Mengistu, S.G.; Creed, I.F.; Webster, K.L.; Enanga, E.; Beall, F.D. Searching for similarity in topographic controls on carbon, nitrogen and phosphorus export from forested headwater catchments. Hydrol. Process. 2014, 28, 3201–3216. [Google Scholar] [CrossRef]
- Saunois, M.; Bousquet, P.; Poulter, B.; Peregon, A.; Ciais, P.; Canadell, J.G.; Dlugokencky, E.J.; Etiope, G.; Bastviken, D.; Houweling, S.; et al. The Global Methane Budget: 2000–2012. Earth Syst. Sci. Data Discuss. 2016, 8, 697–751. [Google Scholar] [CrossRef]
- Meng, L.; Hess, P.G.M.; Mahowald, N.M.; Yavitt, J.B.; Riley, W.J.; Subin, Z.M.; Lawrence, D.M.; Swenson, S.C.; Jauhiainen, J.; Fuka, D.R. Sensitivity of wetland methane emissions to model assumptions: Application and model testing against site observations. Biogeosciences 2012, 9, 2793–2819. [Google Scholar] [CrossRef]
- Watts, J.D.; Kimball, J.S.; Bartsch, A.; McDonald, K.C. Surface water inundation in the boreal-Arctic: Potential impacts on regional methane emissions. Environ. Res. Lett. 2014, 9. [Google Scholar] [CrossRef]
- Vörösmarty, C.J.; McIntyre, P.B.; Gessner, M.O.; Dudgeon, D.; Prusevich, A.; Green, P.; Glidden, S.; Bunn, S.E.; Sullivan, C.A.; Liermann, C.R.; et al. Global threats to human water security and river biodiversity. Nature 2010, 467, 555–561. [Google Scholar] [CrossRef] [PubMed]
- Pekel, J.-F.; Cottam, A.; Gorelick, N.; Belward, A.S. High-resolution mapping of global surface water and its long-term changes. Nature 2016, 1–19. [Google Scholar] [CrossRef] [PubMed]
- Wulder, M.A.; Masek, J.G.; Cohen, W.B.; Loveland, T.R.; Woodcock, C.E. Opening the archive: How free data has enabled the science and monitoring promise of Landsat. Remote Sens. Environ. 2012, 122, 2–10. [Google Scholar] [CrossRef]
- Torres, R.; Snoeij, P.; Geudtner, D.; Bibby, D.; Davidson, M.; Attema, E.; Potin, P.; Rommen, B.; Floury, N.; Brown, M.; et al. GMES Sentinel-1 mission. Remote Sens. Environ. 2012, 120, 9–24. [Google Scholar] [CrossRef]
- Drusch, M.; Del Bello, U.; Carlier, S.; Colin, O.; Fernandez, V.; Gascon, F.; Hoersch, B.; Isola, C.; Laberinti, P.; Martimort, P.; et al. Sentinel-2: ESA’s Optical High-Resolution Mission for GMES Operational Services. Remote Sens. Environ. 2012, 120, 25–36. [Google Scholar] [CrossRef]
- Feng, M.; Sexton, J.O.; Channan, S.; Townshend, J.R. A global, high-resolution (30-m) inland water body dataset for 2000: First results of a topographic–spectral classification algorithm. Int. J. Digit. Earth 2015, 8947, 1–21. [Google Scholar] [CrossRef]
- Yamazaki, D.; Trigg, M.A.; Ikeshima, D. Development of a global ~90 m water body map using multi-temporal Landsat images. Remote Sens. Environ. 2015, 171, 337–351. [Google Scholar] [CrossRef] [Green Version]
- Carroll, M.; Townshend, J.R.; DiMiceli, C.M.; Noojipady, P.; Sohlberg, R.A. A new global raster water mask at 250 m resolution. Int. J. Digit. Earth 2009, 2, 291–308. [Google Scholar] [CrossRef]
- Schroeder, R.; McDonald, K.; Chapman, B.; Jensen, K.; Podest, E.; Tessler, Z.; Bohn, T.; Zimmermann, R. Development and Evaluation of a Multi-Year Fractional Surface Water Data Set Derived from Active/Passive Microwave Remote Sensing Data. Remote Sens. 2015, 7, 16688–16732. [Google Scholar] [CrossRef]
- Fluet-Chouinard, E.; Lehner, B.; Rebelo, L.M.; Papa, F.; Hamilton, S.K. Development of a global inundation map at high spatial resolution from topographic downscaling of coarse-scale remote sensing data. Remote Sens. Environ. 2015, 158, 348–361. [Google Scholar] [CrossRef]
- Verpoorter, C.; Kutser, T.; Tranvik, L.J. Automated mapping of water bodies using Landsat multispectral data. Limnol. Oceanogr. Methods 2012, 10, 1037–1050. [Google Scholar] [CrossRef]
- Watts, J.D.; Kimball, J.S.; Jones, L.A.; Schroeder, R.; McDonald, K.C. Satellite Microwave remote sensing of contrasting surface water inundation changes within the Arctic-Boreal Region. Remote Sens. Environ. 2012, 127, 223–236. [Google Scholar] [CrossRef]
- Carroll, M.; Wooten, M.; DiMiceli, C.; Sohlberg, R.; Kelly, M. Quantifying Surface Water Dynamics at 30 Meter Spatial Resolution in the North American High Northern Latitudes 1991–2011. Remote Sens. 2016, 8. [Google Scholar] [CrossRef]
- Mueller, N.; Lewis, A.; Roberts, D.; Ring, S.; Melrose, R.; Sixsmith, J.; Lymburner, L.; McIntyre, A.; Tan, P.; Curnow, S.; Ip, A. Water observations from space: Mapping surface water from 25 years of Landsat imagery across Australia. Remote Sens. Environ. 2016, 174, 341–352. [Google Scholar] [CrossRef]
- Lehner, B.; Döll, P. Development and validation of a global database of lakes, reservoirs and wetlands. J. Hydrol. 2004, 296, 1–22. [Google Scholar] [CrossRef]
- Jones, J.W. Efficient wetland surface water detection and monitoring via landsat: Comparison with in situ data from the everglades depth estimation network. Remote Sens. 2015, 7, 12503–12538. [Google Scholar] [CrossRef]
- McFeeters, S.K. The use of the Normalized Difference Water Index (NDWI) in the delineation of open water features. Int. J. Remote Sens. 1996, 17, 1425–1432. [Google Scholar] [CrossRef]
- Xu, H. Modification of normalised difference water index (NDWI) to enhance open water features in remotely sensed imagery. Int. J. Remote Sens. 2006, 27, 3025–3033. [Google Scholar] [CrossRef]
- Feyisa, G.L.; Meilby, H.; Fensholt, R.; Proud, S.R. Automated Water Extraction Index: A new technique for surface water mapping using Landsat imagery. Remote Sens. Environ. 2014, 140, 23–35. [Google Scholar] [CrossRef]
- Xie, H.; Luo, X.; Xu, X.; Pan, H.; Tong, X. Automated Subpixel Surface Water Mapping from Heterogeneous Urban Environments Using Landsat 8 OLI Imagery. Remote Sens. 2016, 8. [Google Scholar] [CrossRef]
- Tulbure, M.G.; Broich, M.; Stehman, S.V.; Kommareddy, A. Surface water extent dynamics from three decades of seasonally continuous Landsat time series at subcontinental scale in a semi-arid region. Remote Sens. Environ. 2016, 178, 142–157. [Google Scholar] [CrossRef]
- Díaz-Delgado, R.; Aragonés, D.; Afán, I.; Bustamante, J. Long-Term Monitoring of the Flooding Regime and Hydroperiod of Doñana Marshes with Landsat Time Series (1974–2014). Remote Sens. 2016, 8. [Google Scholar] [CrossRef]
- Tulbure, M.G.; Broich, M. Spatiotemporal dynamic of surface water bodies using Landsat time-series data from 1999 to 2011. ISPRS J. Photogramm. Remote Sens. 2013, 79, 44–52. [Google Scholar] [CrossRef]
- Fisher, A.; Flood, N.; Danaher, T. Landsat water index methods for automated water classification in eastern Australia. Remote Sens. Environ. 2016, 175, 167–182. [Google Scholar] [CrossRef]
- Rover, J.; Wylie, B.K.; Ji, L. A self-trained classification technique for producing 30 m percent-water maps from Landsat data. Int. J. Remote Sens. 2010, 31, 2197–2203. [Google Scholar] [CrossRef]
- Vanderhoof, M.K.; Christensen, J.R.; Alexander, L.C. Patterns and drivers for wetland connections in the Prairie Pothole Region, United States. Wetl. Ecol. Manag. 2016, 25, 275–297. [Google Scholar] [CrossRef]
- Sexton, J.O.; Song, X.-P.; Feng, M.; Noojipady, P.; Anand, A.; Huang, C.; Kim, D.-H.; Collins, K.M.; Channan, S.; Dimiceli, C.; et al. Global, 30-m resolution continuous fields of tree cover: Landsat-based rescaling of MODIS Vegetation Continuous Fields with lidar-based estimates of error. Int. J. Digit. Earth 2013, 8947. [Google Scholar] [CrossRef]
- Sexton, J.O.; Song, X.-P.; Huang, C.; Channan, S.; Baker, M.E.; Townshend, J.R. Urban growth of the Washington, D.C.-Baltimore, MD metropolitan region from 1984 to 2010 by annual, Landsat-based estimates of impervious cover. Remote Sens. Environ. 2013, 129, 42–53. [Google Scholar] [CrossRef]
- Huang, C.; Peng, Y.; Lang, M.W.; Yeo, I.Y.; McCarty, G. Wetland inundation mapping and change monitoring using Landsat and airborne LiDAR data. Remote Sens. Environ. 2014, 141, 231–242. [Google Scholar] [CrossRef]
- Halabisky, M.; Moskal, L.M.; Gillespie, A.; Hannam, M. Reconstructing semi-arid wetland surface water dynamics through spectral mixture analysis of a time series of Landsat satellite images (1984–2011). Remote Sens. Environ. 2016, 177, 171–183. [Google Scholar] [CrossRef]
- Li, S.; Sun, D.; Yu, Y.; Csiszar, I.; Stefanidis, A.; Goldberg, M.D. A new short-wave infrared (SWIR) method for quantitative water fraction derivation and evaluation with EOS/MODIS and landsat/TM data. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1852–1862. [Google Scholar] [CrossRef]
- Jin, H.; Huang, C.; Lang, M.W.; Yeo, I.-Y.; Stehman, S.V. Monitoring of wetland inundation dynamics in the Delmarva Peninsula using Landsat time-series imagery from 1985 to 2011. Remote Sens. Environ. 2017, 190, 26–41. [Google Scholar] [CrossRef]
- Tiner, R.W. Geographically isolated wetlands of the United States. Wetlands 2003, 23, 494–516. [Google Scholar] [CrossRef]
- Gala, T.S.; Aldred, D.A.; Carlyle, S.; Creed, I.F. Topographically based spatially averaging of SAR data improves performance of soil moisture models. Remote Sens. Environ. 2011, 115, 3507–3516. [Google Scholar] [CrossRef]
- Clark, R.B.; Creed, I.F.; Sass, G.Z. Mapping hydrologically sensitive areas on the Boreal Plain: A multitemporal analysis of ERS synthetic aperture radar data. Int. J. Remote Sens. 2009, 30, 2619–2635. [Google Scholar] [CrossRef]
- Stewart, R.E.; Kantrud, H.A. Vegetation of Prairie Potholes, North Dakota, in Relation to Quality of Water and Other Environmental Factors; U.S. Geological Survey: Reston, VA, USA, 1972; Volume 585.
- Miller, B.A.; Crumpton, W.G.; van der Valk, A.G. Spatial Distribution of Historical Wetland Classes on the Des Moines Lobe, Iowa. Wetlands 2009, 29, 1146–1152. [Google Scholar] [CrossRef]
- Van Meter, K.J.; Basu, N.B. Signatures of human impact: Size distributions and spatial organization of wetlands in the Prairie Pothole landscape. Ecol. Appl. 2015, 25, 451–465. [Google Scholar] [CrossRef] [PubMed]
- Warner, B.G.; Asada, T. Knowledge Gaps and Challenges in Wetlands under Climate Change in Canada. In Climate Change and Managed Ecosystems; Bhatti, J.S., Lal, R., Apps, M.J., Price, M.A., Eds.; Taylor & Francis: Boca Raton, FL, USA, 2006; pp. 355–374. [Google Scholar]
- Dahl, T.E. Status and Trends of Prairie Wetlands in the United States 2004 to 2009; U.S. Department of the Interior, Fish and Wildlife Service: Washington, DC, USA, 2014.
- Serran, J.N.; Creed, I.F. New mapping techniques to estimate the preferential loss of small wetlands on prairie landscapes. Hydrol. Process. 2016, 30, 396–409. [Google Scholar] [CrossRef]
- Creed, I.F.; Miller, J.; Aldred, D.; Adams, J.K.; Spitale, S.; Bourbonniere, R.A. Hydrologic profiling for greenhouse gas effluxes from natural grasslands in the prairie pothole region of Canada. J. Geophys. Res. Biogeosci. 2013, 118, 680–697. [Google Scholar] [CrossRef]
- Marton, J.M.; Creed, I.F.; Lewis, D.B.; Lane, C.R.; Basu, N.B.; Cohen, M.J.; Craft, C.B. Geographically isolated wetlands are important biogeochemical reactors on the landscape. Bioscience 2015, 65, 408–418. [Google Scholar] [CrossRef]
- Rains, M.C.; Leibowitz, S.G.; Cohen, M.J.; Creed, I.F.; Golden, H.E.; Jawitz, J.W.; Kalla, P.; Lane, C.R.; Lang, M.W.; Mclaughlin, D.L. Geographically isolated wetlands are part of the hydrological landscape. Hydrol. Process. 2016, 30, 153–160. [Google Scholar] [CrossRef]
- Golden, H.; Creed, I.F.; Ali, G.; Basu, N.; Neff, B.; Rains, M.; McLaughlin, D.; Alexander, L.; Ameli, A.; Christensen, J.; et al. Scientific tools for integrating geographically isolated wetlands into land management decisions. Front. Ecol. Environ. 2017, in press. [Google Scholar]
- Gleason, R.A.; Euliss, N.H.; Tangen, B.A.; Laubhan, M.K.; Browne, B.A. USDA conservation program and practice effects on wetland ecosystem services in the Prairie Pothole Region Source. Ecol. Appl. 2016, 21, S35–S81. [Google Scholar]
- Badiou, P.; McDougal, R.; Pennock, D.; Clark, B. Greenhouse gas emissions and carbon sequestration potential in restored wetlands of the Canadian prairie pothole region. Wetl. Ecol. Manag. 2011, 19, 237–256. [Google Scholar] [CrossRef]
- Puchniak Begley, A.J.; Gray, B.T.; Paszkowski, C.A. A comparison of restored and natural wetlands as habitat for birds in the Prairie Pothole Region of Saskatchewan, Canada. Raffles Bull. Zool. 2012, 173–187. [Google Scholar]
- Lang, M.W.; McCarty, G.W. Lidar intensity for improved detection of inundation below the forest canopy. Wetlands 2009, 29, 1166–1178. [Google Scholar] [CrossRef]
- Dahl, T.E. Wetlands Losses in the United States: 1780’s to 1980’s; Department of the Interior, Fish and Wildlife Service: Washington, DC, USA, 1990.
- Fisher, T.R.; Benitez, J.A.; Lee, K.; Sutton, A.J. History of land cover change and biogeochemical impacts in the Choptank River basin in the mid-Atlantic region of the US. Int. J. Remote Sens. 2006, 27, 3683–3703. [Google Scholar] [CrossRef]
- Fenstermacher, D.E.; Rabenhorst, M.C.; Lang, M.W.; McCarty, G.W.; Needelman, B.A. Carbon in Natural, Cultivated, and Restored Depressional Wetlands in the Mid-Atlantic Coastal Plain. J. Environ. Qual. 2016, 45, 743–750. [Google Scholar] [CrossRef] [PubMed]
- Jones, J.W. Image and in situ data integration to derive sawgrass density for surface flow modelling in the Everglades, Florida, USA. Remote Sens. Hydrol. 2000, 2000, 507–512. [Google Scholar]
- Jones, J.W.; Hall, A.; Smith, T.J.; Foster, A. Wetland fire scar monitoring using Landsat Archive data for the Everglades. Fire Ecol. 2013, 9, 133–150. [Google Scholar] [CrossRef]
- Carter, V.; Rybicki, N.B.; Reel, J.T.; Ruhl, H.A.; Stewart, D.W.; Jones, J.W. Classification of vegetation for surface-water flow models in Taylor Slough, Everglades National Park. In Proceedings of the Third International Symposium on Ecohydraulics, Salt Lake City, UT, USA, 12–16 July 1999. [Google Scholar]
- Sumner, D.M.; Jacobs, J.M. Utility of Penman-Monteith, Priestley-Taylor, reference evapotranspiration, and pan evaporation methods to estimate pasture evapotranspiration. J. Hydrol. 2005, 308, 81–104. [Google Scholar] [CrossRef]
- Snyder, G.H.; Davidson, J.M. Everglades Agriculture: Past, Present and Future. In Everglades: The Ecosystem and Its Restoration; Davis, S.M., Ogden, J.C., Eds.; St. Lucie Press: Delray Beach, FL, USA, 1994; pp. 85–115. [Google Scholar]
- USACOE Comprehensive Everglades Restoration Plan (CERP). Available online: http://www.saj.usace.army.mil/Portals/44/docs/FactSheets/CERP_FS_March2015_revised.pdf (accessed on 5 May 2017).
- Masek, J.G.; Vermote, E.F.; Saleous, N.E.; Wolfe, R.; Hall, F.G.; Huemmrich, K.F.; Gao, F.; Kutler, J.; Lim, T.K. A landsat surface reflectance dataset for North America, 1990–2000. IEEE Geosci. Remote Sens. Lett. 2006, 3, 68–72. [Google Scholar] [CrossRef]
- Vermote, E.; Justice, C.; Claverie, M.; Franch, B. Preliminary analysis of the performance of the Landsat 8/OLI land surface reflectance product. Remote Sens. Environ. 2016, 185, 46–56. [Google Scholar] [CrossRef]
- Zhu, Z.; Woodcock, C.E. Automated cloud, cloud shadow, and snow detection in multitemporal Landsat data: An algorithm designed specifically for monitoring land cover change. Remote Sens. Environ. 2014, 152, 217–234. [Google Scholar] [CrossRef]
- Zhu, Z.; Wang, S.; Woodcock, C.E. Improvement and expansion of the Fmask algorithm: Cloud, cloud shadow, and snow detection for Landsats 4–7, 8, and Sentinel 2 images. Remote Sens. Environ. 2015, 159, 269–277. [Google Scholar] [CrossRef]
- Jones, J.W. The Dynamic Surface Water Extent (DSWE) Evaluation Strategy. In Proceedings of the European Geoscience Union Annual Meeting, Vienna, Austria, 23–28 April 2017. [Google Scholar]
- Tucker, C.J. Red and photographic infrared linear combinations for monitoring vegetation. Remote Sens. Environ. 1979, 8, 127–150. [Google Scholar] [CrossRef]
- Crist, E.P. A TM Tasseled Cap equivalent transformation for reflectance factor data. Remote Sens. Environ. 1985, 17, 301–306. [Google Scholar] [CrossRef]
- Natural Resources Canada Regional, National and International Climate Modeling. Available online: https://cfs.nrcan.gc.ca/projects/3/2 (accessed on 11 July 2017).
- Lang, M.W.; Kasischke, E.S.; Prince, S.D.; Pittman, K.W. Assessment of C-band synthetic aperture radar data for mapping and monitoring Coastal Plain forested wetlands in the Mid-Atlantic Region, U.S.A. Remote Sens. Environ. 2008, 112, 4120–4130. [Google Scholar] [CrossRef]
- Telis, P.A. The Everglades Depth Estimation Network (EDEN) for Support of Ecological and Biological Assessments; U.S. Geological Survey: Reston, VA, USA, 2006.
- Cazals, C.; Rapinel, S.; Frison, P.-L.; Bonis, A.; Mercier, G.; Mallet, C.; Corgne, S.; Rudant, J.-P. Mapping and Characterization of Hydrological Dynamics in a Coastal Marsh Using High Temporal Resolution Sentinel-1A Images. Remote Sens. 2016, 8. [Google Scholar] [CrossRef]
- South Florida Water Management District 2007–08 Miami-Dade 5-ft DEM, v1. Available online: http://apps.sfwmd.gov/gisapps/sfwmdxwebdc/dataview.asp?query=unq_id=2116 (accessed on 17 July 2017).
- Gómez-Rodríguez, C.; Bustamante, J.; Díaz-Paniagua, C. Evidence of hydroperiod shortening in a preserved system of temporary ponds. Remote Sens. 2010, 2, 1439–1462. [Google Scholar] [CrossRef] [Green Version]
- Frohn, R.C.; D’amico, E.; Lane, C.R.; Autrey, B.; Rhodus, J.; Liu, H. Multi-temporal sub-pixel landsat ETM+ classification of isolated wetlands in cuyahoga county, OHIO, USA. Wetlands 2012, 32, 289–299. [Google Scholar] [CrossRef]
- Reschke, J.; Hüttich, C. Continuous field mapping of Mediterranean wetlands using sub-pixel spectral signatures and multi-temporal Landsat data. Int. J. Appl. Earth Obs. Geoinf. 2014, 28, 220–229. [Google Scholar] [CrossRef]
- Wulder, M.A.; Coops, N.C. Satellites: Make Earth observations open access. Nature 2014, 513, 30–31. [Google Scholar] [CrossRef] [PubMed]
- Nemani, R.; Votava, P.; Michaelis, A.; Melton, F.; Milesi, C. Collaborative Super computing for Global Change Science. Eos Trans. Am. Geophys. Union 2011, 92, 109–116. [Google Scholar] [CrossRef]
- Neigh, C.; Nickeson, J. High-Resolution Satellite Data Open for Government Research. Eos Trans. Am. Geophys. Union 2013, 94, 121–123. [Google Scholar] [CrossRef]
- Downing, J.A.; Prairie, Y.T.; Cole, J.J.; Duarte, C.M.; Tranvik, L.J.; Striegl, R.G.; McDowell, W.H.; Kortelainen, P.; Caraco, N.F.; Melack, J.M. The global abundance and size distribution of lakes, ponds, and impoundments. Limnol. Oceanogr. 2006, 51, 2388–2397. [Google Scholar] [CrossRef]
- Downing, J.A. Emerging global role of small lakes and ponds: Little things mean a lot. Limnetica 2010, 29, 9–24. [Google Scholar]
- Verpoorter, C.; Kutser, T.; Seekell, D.A.; Tranvik, L.J. A global inventory of lakes based on high-resolution satellite imagery. Geophys. Res. Lett. 2014, 41, 6396–6402. [Google Scholar] [CrossRef]
- Shine, K.P.; Derwent, R.G.; Wuebbles, D.J.; Morcrette, J.-J. Radiative Forcing of Climate; Cambridge University Press, for IPCC: Cambridge, UK, 1990. [Google Scholar]
- Intergovernmental Panel on Climate Change (IPCC). Climate Change 2007 Synthesis Report; Intergovernmental Panel on Climate Change: Geneve, Switzerland, 2007. [Google Scholar]
- Mitsch, W.J.; Gosselink, J.G. Wetlands, 5th ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2015. [Google Scholar]
- Kirschke, S.; Bousquet, P.; Ciais, P.; Saunois, M.; Canadell, J.G.; Dlugokencky, E.J.; Bergamaschi, P.; Bergmann, D.; Blake, D.R.; Bruhwiler, L.; et al. Three decades of global methane sources and sinks. Nat. Geosci. 2013, 6, 813–823. [Google Scholar] [CrossRef]
- Melton, J.R.; Wania, R.; Hodson, E.L.; Poulter, B.; Ringeval, B.; Spahni, R.; Bohn, T.; Avis, C.A.; Chen, G.; Eliseev, A.V.; et al. Present state of global wetland extent and wetland methane modelling: Methodology of a model inter-comparison project (WETCHIMP). Geosci. Model Dev. 2013, 6, 617–641. [Google Scholar] [CrossRef]
- Freeman, M.C.; Pringle, C.M.; Jackson, C.R. Hydrologic connectivity and the contribution of stream headwaters to ecological integrity at regional scales. J. Am. Water Resour. Assoc. 2007, 43, 5–14. [Google Scholar] [CrossRef]
- Bishop-Taylor, R.; Tulbure, M.G.; Broich, M. Surface water network structure, landscape resistance to movement and flooding vital for maintaining ecological connectivity across Australia’s largest river basin. Landsc. Ecol. 2015, 30, 2045–2065. [Google Scholar] [CrossRef]
- Lang, M.W.; McDonough, O.; McCarty, G.; Oesterling, R.; Wilen, B. Enhanced detection of wetland-stream connectivity using lidar. Wetlands 2012, 32, 461–473. [Google Scholar] [CrossRef]
- Berger, M.; Moreno, J.; Johannessen, J.A.; Levelt, P.F.; Hanssen, R.F. ESA’s sentinel missions in support of Earth system science. Remote Sens. Environ. 2012, 120, 84–90. [Google Scholar] [CrossRef]
- Hong, S.H.; Wdowinski, S.; Kim, S.W.; Won, J.S. Multi-temporal monitoring of wetland water levels in the Florida Everglades using interferometric synthetic aperture radar (InSAR). Remote Sens. Environ. 2010, 114, 2436–2447. [Google Scholar] [CrossRef]
- Lang, M.W.; Kasischke, E.S. Using C-band synthetic aperture radar data to monitor forested wetland hydrology in Maryland’s coastal plain, USA. IEEE Trans. Geosci. Remote Sens. 2008, 46, 535–546. [Google Scholar] [CrossRef]









| Site | Path/Row | Sensor(s) | Date(s) | Number |
|---|---|---|---|---|
| PPR | 37/25, 38/25, 36/25, 37/24, 36/24, 37/23, 36/23 | Landsat 5 TM, Landsat 7 ETM+ | All available dates between 04/2005 and 09/2005 inclusive | 96 |
| DEL | 14/33 | Landsat 5 TM | 2007-03-29, 2009-03-18 | 2 |
| EVE | 15/42 | Landsat 5 TM, Landsat 7 ETM+, Landsat 8 OLI | All available dates | 894 |
| Band Name | Abbreviation | Band Index | ||
|---|---|---|---|---|
| LT5 | LE7 | LC8 | ||
| Blue | B | 1 | 1 | 2 |
| Green | G | 2 | 2 | 3 |
| Red | R | 3 | 3 | 4 |
| Near Infrared | NIR | 4 | 4 | 5 |
| Shortwave Infrared 1 | SWIR1 | 5 | 5 | 6 |
| Shortwave Infrared 2 | SWIR2 | 7 | 7 | 7 |
| Index | Abbreviation | Formula | Reference |
|---|---|---|---|
| Normalized Difference Water Index | NDWI | [29] | |
| Modified NDWI | MNDWI | [30] | |
| Normalized Difference Vegetation Index | NDVI | [76] | |
| Tasseled Cap Indices | TCB,TCG,TCW | – | [77] |
| TCW-TCG Difference | TCWGD | [41] |
| Site | Data Source(s) | Measurement Target | Accuracy Metric |
|---|---|---|---|
| PPR | Inundated area polygons | Inundated area | RMSE |
| nRMSE | |||
| DEL | Gridded LiDAR intensity | SWF | nRMSE |
| EVE | Water depth gages + DEM | SWF | nRMSE |
| EDEN Station Name | Longitude | Latitude | Average Ground Elevation (ft) | Average Ground Elevation (m) |
|---|---|---|---|---|
| ANGEL | −80.5417 | 25.6226 | 4.73 | 1.442 |
| C111 | −80.5200 | 25.2944 | 0.02 | 0.006 |
| CP | −80.7039 | 25.2275 | −1.49 | −0.454 |
| E112 | −80.6097 | 25.4239 | 2.43 | 0.741 |
| E146 | −80.6663 | 25.2526 | −0.46 | −0.290 |
| EP1R | −80.4531 | 25.2875 | −0.88 | −0.268 |
| EPSW | −80.5081 | 25.2714 | −0.21 | −0.064 |
| EVER4 | −80.5467 | 25.3388 | −0.5 | −0.152 |
| EVER6 | −80.5114 | 25.2969 | 0.34 | 0.104 |
| G-3437 | −80.5671 | 25.5670 | 5.27 | 1.606 |
| G-3626 | −80.5113 | 25.6186 | 5.75 | 1.753 |
| G-3628 | −80.5347 | 25.5941 | 5.55 | 1.692 |
| G-3761 | −80.4335 | 25.8417 | 3.25 | 0.991 |
| NCL | −80.7444 | 25.2425 | −1.29 | −0.393 |
| NTS1 | −80.5928 | 25.4367 | 3.32 | 0.884 |
| NTS10 | −80.6050 | 25.4603 | 3.89 | 1.155 |
| R3110 | −80.6261 | 25.4461 | 3.65 | 1.113 |
| Dataset | Measure | Value | n |
|---|---|---|---|
| Prairie Pothole Region | |||
| Class 4 ponds | RMSE | 0.61 ha | 16 |
| nRMSE | 0.23 | ||
| Class 5 ponds | RMSE | 0.38 ha | 7 |
| nRMSE | 0.18 | ||
| All | RMSE | 0.55 ha | 23 |
| nRMSE | 0.18 | ||
| Delmarva | |||
| LiDAR-2007 | nRMSE | 0.15 | -- |
| LiDAR-2009 | nRMSE | 0.11 | -- |
| Everglades | |||
| Gage sites | median RMSE | 0.19 | 2815 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
DeVries, B.; Huang, C.; Lang, M.W.; Jones, J.W.; Huang, W.; Creed, I.F.; Carroll, M.L. Automated Quantification of Surface Water Inundation in Wetlands Using Optical Satellite Imagery. Remote Sens. 2017, 9, 807. https://doi.org/10.3390/rs9080807
DeVries B, Huang C, Lang MW, Jones JW, Huang W, Creed IF, Carroll ML. Automated Quantification of Surface Water Inundation in Wetlands Using Optical Satellite Imagery. Remote Sensing. 2017; 9(8):807. https://doi.org/10.3390/rs9080807
Chicago/Turabian StyleDeVries, Ben, Chengquan Huang, Megan W. Lang, John W. Jones, Wenli Huang, Irena F. Creed, and Mark L. Carroll. 2017. "Automated Quantification of Surface Water Inundation in Wetlands Using Optical Satellite Imagery" Remote Sensing 9, no. 8: 807. https://doi.org/10.3390/rs9080807
APA StyleDeVries, B., Huang, C., Lang, M. W., Jones, J. W., Huang, W., Creed, I. F., & Carroll, M. L. (2017). Automated Quantification of Surface Water Inundation in Wetlands Using Optical Satellite Imagery. Remote Sensing, 9(8), 807. https://doi.org/10.3390/rs9080807