Satellite-Based Inversion and Field Validation of Autotrophic and Heterotrophic Respiration in an Alpine Meadow on the Tibetan Plateau
Abstract
:1. Introduction
2. Materials and Methods
2.1. Site Descriptions
2.2. Meteorological, Soil and Vegetation Measurements
2.3. Eddy Covariance-Based Measurements
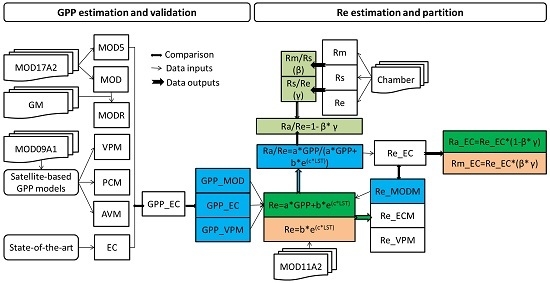
2.4. Satellite-Based Products
2.5. Satellite-Based GPP Estimations
2.6. Satellite-Based Re Estimations
2.7. Chamber-Based Re Estimations
2.8. Components Partitioning of Re
2.9. Statistical Analysis
3. Results
3.1. Meteorological and Vegetation Conditions
3.2. Satellite-Based GPP Estimations
3.3. Satellite-Based Re estimations
3.4. Re Partitioning and Chamber-Based Validation
4. Discussion
4.1. Variability of Re Components
4.2. Temperature Sensitivity of Re Components
4.3. Methods Applications and Uncertainty
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Beer, C.; Reichstein, M.; Tomelleri, E.; Ciais, P.; Jung, M.; Carvalhais, N.; Rodenbeck, C.; Arain, M.A.; Baldocchi, D.; Bonan, G.B.; et al. Terrestrial gross carbon dioxide uptake: Global distribution and covariation with climate. Science 2010, 329, 834–838. [Google Scholar] [CrossRef] [PubMed]
- Running, S.W.; Thornton, P.E.; Nemani, R.; Glassy, J.M. Global terrestrial gross and net primary productivity from the earth observing system. In Methods in Ecosystem Science; Sala, O., Jackson, R., Mooney, H., Howarth, R., Eds.; Springer: New York, NY, USA, 2000; pp. 44–57. [Google Scholar]
- Gitelson, A.A.; Viña, A.; Verma, S.B.; Rundquist, D.C.; Arkebauer, T.J.; Keydan, G.; Leavitt, B.; Ciganda, V.; Burba, G.G.; Suyker, A.E. Relationship between gross primary production and chlorophyll content in crops: Implications for the synoptic monitoring of vegetation productivity. J. Geophys. Res. Atmos. 2006, 111. [Google Scholar] [CrossRef]
- Chen, B.X.; Zhang, X.Z.; Tao, J.; Wu, J.S.; Wang, J.S.; Shi, P.L.; Zhang, Y.J.; Yu, C.Q. The impact of climate change and anthropogenic activities on alpine grassland over the qinghai-tibet plateau. Agric. For. Meteorol. 2014, 189, 11–18. [Google Scholar] [CrossRef]
- Zhou, X.; Wan, S.; Luo, Y. Source components and interannual variability of soil CO2 efflux under experimental warming and clipping in a grassland ecosystem. Glob. Chang. Biol. 2007, 13, 761–775. [Google Scholar]
- Kato, T.; Tang, Y.H.; Gu, S.; Hirota, M.; Cui, X.Y.; Du, M.Y.; Li, Y.N.; Zhao, X.Q.; Oikawa, T. Seasonal patterns of gross primary production and ecosystem respiration in an alpine meadow ecosystem on the qinghai-tibetan plateau. J. Geophys. Res. Atmos. 2004, 109. [Google Scholar] [CrossRef]
- Rey, A.; Pegoraro, E.; Tedeschi, V.; De Parri, I.; Jarvis, P.G.; Valentini, R. Annual variation in soil respiration and its components in a coppice oak forest in central italy. Glob. Chang. Biol. 2002, 8, 851–866. [Google Scholar] [CrossRef]
- Raich, J.W.; Schlesinger, W.H. The global carbon-dioxide flux in soil respiration and its relationship to vegetation and climate. Tellus Ser. B Chem. Phys. Meteorol. 1992, 44, 81–99. [Google Scholar] [CrossRef]
- Hicks Pries, C.E.; Schuur, E.A.G.; Crummer, K.G. Thawing permafrost increases old soil and autotrophic respiration in tundra: Partitioning ecosystem respiration using δ13c and ∆14c. Glob. Chang. Biol. 2013, 19, 649–661. [Google Scholar] [CrossRef] [PubMed]
- Buchmann, N. Biotic and abiotic factors controlling soil respiration rates in picea abies stands. Soil Biol. Biochem. 2000, 32, 1625–1635. [Google Scholar] [CrossRef]
- Bond-Lamberty, B.; Wang, C.; Gower, S.T. A global relationship between the heterotrophic and autotrophic components of soil respiration? Glob. Chang. Biol. 2004, 10, 1756–1766. [Google Scholar] [CrossRef]
- Hanson, P.J.; Edwards, N.T.; Garten, C.T.; Andrews, J.A. Separating root and soil microbial contributions to soil respiration: A review of methods and observations. Biogeochemistry 2000, 48, 115–146. [Google Scholar] [CrossRef]
- Ni, J. Carbon storage in grasslands of China. J. Arid Environ. 2002, 50, 205–218. [Google Scholar] [CrossRef]
- Saito, M.; Kato, T.; Tang, Y. Temperature controls ecosystem CO2 exchange of an alpine meadow on the northeastern tibetan plateau. Glob. Chang. Biol. 2009, 15, 221–228. [Google Scholar] [CrossRef]
- Chen, H.; Zhu, Q.; Peng, C.; Wu, N.; Wang, Y.; Fang, X.; Gao, Y.; Zhu, D.; Yang, G.; Tian, J.; et al. The impacts of climate change and human activities on biogeochemical cycles on the qinghai-tibetan plateau. Glob. Chang. Biol. 2013, 19, 2940–2955. [Google Scholar] [CrossRef] [PubMed]
- Zheng, D.; Zhang, Q.; Wu, S. Mountain Geoecology and Sustainable Development of the Tibetan Plateau; Springer Science & Business Media: Berlin, Germany, 2000; Volume 57. [Google Scholar]
- IPCC—Intergovernmental Panel on Climate Change. Impacts, Adaptation and Vulnerability: Regional Aspects; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Liu, X.; Chen, B. Climatic warming in the tibetan plateau during recent decades. Int. J. Climatol. 2000, 20, 1729–1742. [Google Scholar] [CrossRef]
- Zhao, L.; Li, Y.; Xu, S.; Zhou, H.; Gu, S.; Yu, G.; Zhao, X. Diurnal, seasonal and annual variation in net ecosystem CO2 exchange of an alpine shrubland on qinghai-tibetan plateau. Glob. Chang. Biol. 2006, 12, 1940–1953. [Google Scholar] [CrossRef]
- Li, J.; Fang, X. Uplift of the tibetan plateau and environmental changes. Chin. Sci. Bull. 1999, 44, 2117–2124. [Google Scholar] [CrossRef]
- Vesala, T.; Kljun, N.; Rannik, Ü.; Rinne, J.; Sogachev, A.; Markkanen, T.; Sabelfeld, K.; Foken, T.; Leclerc, M.Y. Flux and concentration footprint modelling: State of the art. Environ. Pollut. 2008, 152, 653–666. [Google Scholar] [CrossRef] [PubMed]
- Baldocchi, D.D. Assessing the eddy covariance technique for evaluating carbon dioxide exchange rates of ecosystems: Past, present and future. Glob. Chang. Biol. 2003, 9, 479–492. [Google Scholar] [CrossRef]
- Baldocchi, D.; Falge, E.; Gu, L.H.; Olson, R.; Hollinger, D.; Running, S.; Anthoni, P.; Bernhofer, C.; Davis, K.; Evans, R.; et al. Fluxnet: A new tool to study the temporal and spatial variability of ecosystem-scale carbon dioxide, water vapor, and energy flux densities. Bull. Am. Meteorol. Soc. 2001, 82, 2415–2434. [Google Scholar] [CrossRef]
- Reichstein, M.; Falge, E.; Baldocchi, D.; Papale, D.; Aubinet, M.; Berbigier, P.; Bernhofer, C.; Buchmann, N.; Gilmanov, T.; Granier, A.; et al. On the separation of net ecosystem exchange into assimilation and ecosystem respiration: Review and improved algorithm. Glob. Chang. Biol. 2005, 11, 1424–1439. [Google Scholar] [CrossRef]
- Niu, B.; He, Y.; Zhang, X.; Du, M.; Shi, P.; Sun, W.; Zhang, L. CO2 exchange in an alpine swamp meadow on the central Tibetan Plateau. Wetlands 2017, 37, 525–543. [Google Scholar] [CrossRef]
- Shi, P.L.; Sun, X.M.; Xu, L.L.; Zhang, X.Z.; He, Y.T.; Zhang, D.Q.; Yu, G.R. Net ecosystem CO2 exchange and controlling factors in a steppe—Kobresia meadow on the tibetan plateau. Sci. China Ser. D 2006, 49, 207–218. [Google Scholar] [CrossRef]
- Zhao, L.; Li, J.; Xu, S.; Zhou, H.; Li, Y.; Gu, S.; Zhao, X. Seasonal variations in carbon dioxide exchange in an alpine wetland meadow on the qinghai-tibetan plateau. Biogeosciences 2010, 7, 1207–1221. [Google Scholar] [CrossRef]
- Xiao, X.; Hollinger, D.; Aber, J.; Goltz, M.; Davidson, E.A.; Zhang, Q.; Moore, B., III. Satellite-based modeling of gross primary production in an evergreen needleleaf forest. Remote Sens. Environ. 2004, 89, 519–534. [Google Scholar] [CrossRef]
- Xiao, X.; Zhang, Q.; Saleska, S.; Hutyra, L.; De Camargo, P.; Wofsy, S.; Frolking, S.; Boles, S.; Keller, M.; Moore, B., III. Satellite-based modeling of gross primary production in a seasonally moist tropical evergreen forest. Remote Sens. Environ. 2005, 94, 105–122. [Google Scholar] [CrossRef]
- Niu, B.; Zhang, X.; He, Y.; Shi, P.; Fu, G.; Du, M.; Zhang, Y.; Zong, N.; Zhang, J.; Wu, J. Satellite-based estimation of gross primary production in an alpine swamp meadow on the tibetan plateau: A multi-model comparison. J. Resour. Ecol. 2017, 8, 57–66. [Google Scholar]
- Heinsch, F.A.; Reeves, M.; Votava, P.; Kang, S.; Milesi, C.; Zhao, M.; Glassy, J.; Jolly, W.M.; Loehman, R.; Bowker, C.F. GPP and NPP (MOD17A2/A3) Products NASA MODIS Land Algorithm; MOD17 User’s Guide; NASA: Washington, DC, USA, 2003; pp. 1–57.
- Running, S.; Mu, Q.; Zhao, M. Mod17a3h MODIS/Terra Net Primary Production Yearly l4 Global 500 M Sin Grid V006; NASA: Washington, DC, USA, 2015.
- Niu, B.; He, Y.; Zhang, X.; Fu, G.; Shi, P.; Du, M.; Zhang, Y.; Zong, N. Tower-based validation and improvement of MODIS gross primary production in an alpine swamp meadow on the tibetan plateau. Remote Sens. 2016, 8, 592. [Google Scholar] [CrossRef]
- Gao, Y.; Yu, G.; Yan, H.; Zhu, X.; Li, S.; Wang, Q.; Zhang, J.; Wang, Y.; Li, Y.; Zhao, L.; et al. A MODIS-based photosynthetic capacity model to estimate gross primary production in northern China and the tibetan plateau. Remote Sens. Environ. 2014, 148, 108–118. [Google Scholar] [CrossRef]
- Li, F.; Wang, X.; Zhao, J.; Zhang, X.; Zhao, Q. A method for estimating the gross primary production of alpine meadows using MODIS and climate data in China. Int. J. Remote Sens. 2013, 34, 8280–8300. [Google Scholar] [CrossRef]
- Dong, J.; Xiao, X.; Wagle, P.; Zhang, G.; Zhou, Y.; Jin, C.; Torn, M.S.; Meyers, T.P.; Suyker, A.E.; Wang, J.; et al. Comparison of four evi-based models for estimating gross primary production of maize and soybean croplands and tallgrass prairie under severe drought. Remote Sens. Environ. 2015, 162, 154–168. [Google Scholar] [CrossRef]
- Liu, J.; Sun, O.J.; Jin, H.; Zhou, Z.; Han, X. Application of two remote sensing gpp algorithms at a semiarid grassland site of north China. J. Plant Ecol. 2011, 4, 302–312. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, L.; Wang, S. Comparison of different gpp models in China using MODIS image and chinaflux data. Remote Sens. 2014, 6, 10215. [Google Scholar] [CrossRef]
- Wagle, P.; Gowda, P.H.; Xiao, X.; Kc, A. Parameterizing ecosystem light use efficiency and water use efficiency to estimate maize gross primary production and evapotranspiration using MODIS evi. Agric. For. Meteorol. 2016, 222, 87–97. [Google Scholar] [CrossRef]
- Fu, G.; Shen, Z.X.; Zhang, X.Z.; Shi, P.L.; He, Y.T.; Zhang, Y.J.; Sun, W.; Wu, J.S.; Zhou, Y.T.; Pan, X. Calibration of MODIS-based gross primary production over an alpine meadow on the tibetan plateau. Can. J. Remote Sens. 2012, 38, 157–168. [Google Scholar] [CrossRef]
- Running, S.W.; Nemani, R.R.; Heinsch, F.A.; Zhao, M.; Reeves, M.; Hashimoto, H. A continuous satellite-derived measure of global terrestrial primary production. BioScience 2004, 54, 547–560. [Google Scholar] [CrossRef]
- Gao, Y.; Yu, G.; Li, S.; Yan, H.; Zhu, X.; Wang, Q.; Shi, P.; Zhao, L.; Li, Y.; Zhang, F.; et al. A remote sensing model to estimate ecosystem respiration in northern China and the tibetan plateau. Ecol. Model. 2015, 304, 34–43. [Google Scholar] [CrossRef]
- Carbone, M.S.; Richardson, A.D.; Chen, M.; Davidson, E.A.; Hughes, H.; Savage, K.E.; Hollinger, D.Y. Constrained partitioning of autotrophic and heterotrophic respiration reduces model uncertainties of forest ecosystem carbon fluxes but not stocks. J. Geophys. Res. Biogeosci. 2016, 121, 2476–2492. [Google Scholar] [CrossRef]
- Huang, N.; Gu, L.H.; Niu, Z. Estimating soil respiration using spatial data products: A case study in a deciduous broadleaf forest in the midwest USA. J. Geophys. Res. Atmos. 2014, 119, 6393–6408. [Google Scholar] [CrossRef]
- Fu, G.; Zhang, X.-Z.; Zhou, Y.-T.; Yu, C.-Q.; Shen, Z.-X. Partitioning sources of ecosystem and soil respiration in an alpine meadow of tibet plateau using regression method. Pol. J. Ecol. 2014, 62, 17–24. [Google Scholar] [CrossRef]
- Kuzyakov, Y. Sources of CO2 efflux from soil and review of partitioning methods. Soil Biol. Biochem. 2006, 38, 425–448. [Google Scholar] [CrossRef]
- Zong, N.; Jiang, J.; Shi, P.; Song, M.; Shen, Z.; Zhang, X. Nutrient enrichment mediates the relationships of soil microbial respiration with climatic factors in an alpine meadow. Sci. World J. 2015, 2015, 11. [Google Scholar] [CrossRef] [PubMed]
- Zong, N.; Shi, P.-L.; Chai, X.; Jiang, J.; Zhang, X.-Z.; Song, M.-H. Responses of ecosystem respiration to nitrogen enrichment and clipping mediated by soil acidification in an alpine meadow. Pedobiologia 2017, 60, 1–10. [Google Scholar] [CrossRef]
- Griffis, T.J.; Black, T.A.; Gaumont-Guay, D.; Drewitt, G.B.; Nesic, Z.; Barr, A.G.; Morgenstern, K.; Kljun, N. Seasonal variation and partitioning of ecosystem respiration in a southern boreal aspen forest. Agric. For. Meteorol. 2004, 125, 207–223. [Google Scholar] [CrossRef]
- Wang, M.; Guan, D.-X.; Han, S.-J.; Wu, J.-L. Comparison of eddy covariance and chamber-based methods for measuring CO2 flux in a temperate mixed forest. Tree Physiol. 2009, 30, 149–163. [Google Scholar] [CrossRef] [PubMed]
- Zha, T.; Xing, Z.; Wang, K.-Y.; Kellomäki, S.; Barr, A.G. Total and component carbon fluxes of a scots pine ecosystem from chamber measurements and eddy covariance. Ann. Bot. 2007, 99, 345–353. [Google Scholar] [CrossRef] [PubMed]
- Burba, G.; Anderson, D. Introduction to the Eddy Covariance Method; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2000. [Google Scholar]
- Li, C.; He, H.L.; Liu, M.; Su, W.; Fu, Y.L.; Zhang, L.M.; Wen, X.F.; Yu, G.R. The design and application of CO2 flux data processing system at chinaflux. Geogr. Inf. Sci. 2008, 10, 557–565. [Google Scholar]
- Yu, G.R.; Wen, X.F.; Sun, X.M.; Tanner, B.D.; Lee, X.H.; Chen, J.Y. Overview of chinaflux and evaluation of its eddy covariance measurement. Agric. For. Meteorol. 2006, 137, 125–137. [Google Scholar] [CrossRef]
- Falge, E.; Baldocchi, D.; Olson, R.; Anthoni, P.; Aubinet, M.; Bernhofer, C.; Burba, G.; Ceulemans, G.; Clement, R.; Dolman, H.; et al. Gap filling strategies for long term energy flux data sets. Agric. For. Meteorol. 2001, 107, 71–77. [Google Scholar] [CrossRef]
- Ruimy, A.; Jarvis, P.G.; Baldocchi, D.D.; Saugier, B. CO2 fluxes over plant canopies and solar radiation: A review. In Advances in Ecological Research; Begon, I.M., Fitter, A.H., Eds.; Academic Press: San Diego, CA, USA, 1995; Volume 26, pp. 1–68. [Google Scholar]
- Lloyd, J.; Taylor, J.A. On the temperature-dependence of soil respiration. Funct. Ecol. 1994, 8, 315–323. [Google Scholar] [CrossRef]
- Van’t Hoff, J.H. ber die zunehmende bedeutung der anorganischen chemie. Vortrag, gehalten auf der 70. Versammlung der gesellschaft deutscher naturforscher und rzte zu düsseldorf. Z. Anorg. Chem. 1898, 18, 1–13. [Google Scholar] [CrossRef]
- Lasslop, G.; Reichstein, M.; Papale, D.; Richardson, A.D.; Arneth, A.; Barr, A.; Stoy, P.; Wohlfahrt, G. Separation of net ecosystem exchange into assimilation and respiration using a light response curve approach: Critical issues and global evaluation. Glob. Chang. Biol. 2010, 16, 187–208. [Google Scholar] [CrossRef]
- Vermote, E. Mod09a1 MODIS/Terra Surface Reflectance 8-Day l3 Global 500 M Sin Grid V006; NASA EOSDIS Land Processes DAAC: Sioux Falls, SD, USA, 2015.
- Wan, Z.; Hook, S.; Hulley, G. Mod11 l2 MODIS/Terra Land Surface Temperature/Emissivity 5-min l2 Swath 1 Km V006; NASA EOSDIS Land Processes DAAC: Sioux Falls, SD, USA, 2015; Volume 6.
- Myneni, R. Mod15a2h MODIS/Terra Leaf Area Index/Fpar 8-Day l4 Global 500 M Sin Grid V006; NASA EOSDIS Land Processes DAAC: Sioux Falls, SD, USA, 2015.
- Monteith, J.L. A reinterpretation of stomatal responses to humidity. Plant Cell Environ. 1995, 18, 357–364. [Google Scholar] [CrossRef]
- Reichstein, M.; Ciais, P.; Papale, D.; Valentini, R.; Running, S.; Viovy, N.; Cramer, W.; Granier, A.; OgÉE, J.; Allard, V.; et al. Reduction of ecosystem productivity and respiration during the european summer 2003 climate anomaly: A joint flux tower, remote sensing and modelling analysis. Glob. Chang. Biol. 2007, 13, 634–651. [Google Scholar] [CrossRef]
- Atlas, R.; Lucchesi, R. File Specific for Geos-Das Celled Output; Goddard Space Flight Center: Greenbelt, MD, USA, 2000.
- Ruimy, A.; Kergoat, L.; Bondeau, A. IhE. Participants OF. ThE. Potsdam NpP. Model Intercomparison. Comparing global models of terrestrial net primary productivity (npp): Analysis of differences in light absorption and light-use efficiency. Glob. Chang. Biol. 1999, 5, 56–64. [Google Scholar] [CrossRef]
- Varlet-Grancher, C.; Bonhomme, R.; Jacob, C.; Artis, P.; Chartier, M. Caracterisation et Evolution de la Structure d’un Couvert vEgetal de Canne A Sucre; Annales Agronomiques: Paris, France, 1980. [Google Scholar]
- Zhang, X.Z.; Zhang, Y.G.; Zhoub, Y.H. Measuring and modelling photosynthetically active radiation in tibet plateau during april-october. Agric. For. Meteorol. 2000, 102, 207–212. [Google Scholar] [CrossRef]
- Hanan, N.P.; Burba, G.; Verma, S.B.; Berry, J.A.; Suyker, A.; Walter-Shea, E.A. Inversion of net ecosystem CO2 flux measurements for estimation of canopy par absorption. Glob. Chang. Biol. 2002, 8, 563–574. [Google Scholar] [CrossRef]
- Xu, L.L.; Zhang, X.Z.; Shi, P.L.; Li, W.H.; He, Y.T. Modeling the maximum apparent quantum use efficiency of alpine meadow ecosystem on tibetan plateau. Ecol. Model. 2007, 208, 129–134. [Google Scholar] [CrossRef]
- Brooks, A.; Farquhar, G.D. Effect of temperature on the CO2/O2 specificity of ribulose-1,5-bisphosphate carboxylase/oxygenase and the rate of respiration in the light. Planta 1985, 165, 397–406. [Google Scholar] [CrossRef] [PubMed]
- Goudriaan, J.; Van Laar, H.; Van Keulen, H.; Louwerse, W. Photosynthesis, CO2 and Plant Production; Springer: Dordrecht, The Netherlands, 1985. [Google Scholar]
- Xiao, X.; Zhang, Q.; Hollinger, D.; Aber, J.; Moore, B. Modeling gross primary production of an evergreen needleleaf forest using MODIS and climate data. Ecol. Appl. 2005, 15, 954–969. [Google Scholar] [CrossRef]
- Yan, H.; Fu, Y.; Xiao, X.; Huang, H.Q.; He, H.; Ediger, L. Modeling gross primary productivity for winter wheat–maize double cropping system using MODIS time series and CO2 eddy flux tower data. Agric. Ecosyst. Environ. 2009, 129, 391–400. [Google Scholar] [CrossRef]
- Hermle, S.; Lavigne, M.B.; Bernier, P.Y.; Bergeron, O.; Paré, D. Component respiration, ecosystem respiration and net primary production of a mature black spruce forest in northern quebec. Tree Phys. 2010, 30, 527–540. [Google Scholar] [CrossRef] [PubMed]
- Parkin, T.B.; Venterea, R.T. Usda-ars gracenet project protocols, chapter 3. Chamber-based trace gas flux measurements. In Sampling Protocols; SanAir Technologies Laboratory, Inc.: Beltsville, MD, USA, 2010; pp. 1–39. [Google Scholar]
- Heinemeyer, A.; Di Bene, C.; Lloyd, A.R.; Tortorella, D.; Baxter, R.; Huntley, B.; Gelsomino, A.; Ineson, P. Soil respiration: Implications of the plant-soil continuum and respiration chamber collar-insertion depth on measurement and modelling of soil CO2 efflux rates in three ecosystems. Eur. J. Soil Sci. 2011, 62, 82–94. [Google Scholar] [CrossRef]
- Davidson, E.A.; Richardson, A.D.; Savage, K.E.; Hollinger, D.Y. A distinct seasonal pattern of the ratio of soil respiration to total ecosystem respiration in a spruce-dominated forest. Glob. Chang. Biol. 2006, 12, 230–239. [Google Scholar] [CrossRef]
- Zhang, P.; Tang, Y.; Hirota, M.; Yamamoto, A.; Mariko, S. Use of a regression method to partition sources of ecosystem respiration in an alpine meadow. Soil Biol. Biochem. 2009, 41, 663–670. [Google Scholar] [CrossRef]
- Li, D.; Zhou, X.; Wu, L.; Zhou, J.; Luo, Y. Contrasting responses of heterotrophic and autotrophic respiration to experimental warming in a winter annual-dominated prairie. Glob. Chang. Biol. 2013, 19, 3553–3564. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Fu, H.; Guo, D.; Li, X.; Wan, C. Partitioning soil respiration and assessing the carbon balance in a setaria italica (l.) beauv. Cropland on the loess plateau, northern China. Soil Biol. Biochem. 2010, 42, 337–346. [Google Scholar] [CrossRef]
- Zhang, D.-Q.; Shi, P.-L.; He, Y.-T.; Xu, L.; Zhang, X.; Zhong, Z. Quantification of soil heterotrophic respiration in the growth period of alpine steppe-meadow on the tibetan plateau. J. Nat. Resour. 2006, 21, 458–464. [Google Scholar]
- Hu, Q.-W.; Wu, Q.; Cao, G.-M.; Li, D.; Long, R.-J.; Wang, Y.-S. Growing season ecosystem respirations and associated component fluxes in two alpine meadows on the tibetan plateau. J. Integr. Plant Biol. 2008, 50, 271–279. [Google Scholar] [CrossRef] [PubMed]
- Geng, Y.; Luo, G. Influencing factors and partitioning of respiration in a leymus chinensis steppe in xilin river basin, inner mongolia, China. J. Geogr. Sci. 2011, 21, 163–175. [Google Scholar] [CrossRef]
- Jassal, R.S.; Black, T.A.; Cai, T.; Morgenstern, K.; Li, Z.; Gaumont-Guay, D.; Nesic, Z. Components of ecosystem respiration and an estimate of net primary productivity of an intermediate-aged douglas-fir stand. Agric. For. Meteorol. 2007, 144, 44–57. [Google Scholar] [CrossRef]
- Högberg, P.; Bhupinderpal, S.; Löfvenius, M.O.; Nordgren, A. Partitioning of soil respiration into its autotrophic and heterotrophic components by means of tree-girdling in old boreal spruce forest. For. Ecol. Manag. 2009, 257, 1764–1767. [Google Scholar] [CrossRef]
- Davidson, E.A.; Trumbore, S.E. Gas diffusivity and production of CO2 in deep soils of the eastern amazon. Tellus B 1995, 47, 550–565. [Google Scholar] [CrossRef]
- Trumbore, S.E.; Bubier, J.L.; Harden, J.W.; Crill, P.M. Carbon cycling in boreal wetlands: A comparison of three approaches. J. Geophys. Res. Atmos. 1999, 104, 27673–27682. [Google Scholar] [CrossRef]
- Davidson, E.A.; Janssens, I.A. Temperature sensitivity of soil carbon decomposition and feedbacks to climate change. Nature 2006, 440, 165–173. [Google Scholar] [CrossRef] [PubMed]
- Mahecha, M.D.; Reichstein, M.; Carvalhais, N.; Lasslop, G.; Lange, H.; Seneviratne, S.I.; Vargas, R.; Ammann, C.; Arain, M.A.; Cescatti, A.; et al. Global convergence in the temperature sensitivity of respiration at ecosystem level. Science 2010, 329, 838–840. [Google Scholar] [CrossRef] [PubMed]
- Tjoelker, M.G.; Oleksyn, J.; Reich, P.B. Modelling respiration of vegetation: Evidence for a general temperature-dependent Q10. Glob. Chang. Biol. 2001, 7, 223–230. [Google Scholar] [CrossRef]
- Yvon-Durocher, G.; Caffrey, J.M.; Cescatti, A.; Dossena, M.; del Giorgio, P.; Gasol, J.M.; Montoya, J.M.; Pumpanen, J.; Staehr, P.A.; Trimmer, M.; et al. Reconciling the temperature dependence of respiration across timescales and ecosystem types. Nature 2012, 487, 472–476. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Piao, S.; Ciais, P.; Janssens, I.A.; Reichstein, M.; Peng, S.; Wang, T. Are ecological gradients in seasonal Q10 of soil respiration explained by climate or by vegetation seasonality? Soil Biol. Biochem. 2010, 42, 1728–1734. [Google Scholar] [CrossRef]
- Wang, W.; Cheng, W.; Wang, S. Forest soil respiration and its heterotrophic and autotrophic components: Global patterns and responses to temperature and precipitation. Soil Biol. Biochem. 2010, 42, 1236–1244. [Google Scholar]
- Wang, X.; Liu, L.; Piao, S.; Janssens, I.A.; Tang, J.; Liu, W.; Chi, Y.; Wang, J.; Xu, S. Soil respiration under climate warming: Differential response of heterotrophic and autotrophic respiration. Glob. Chang. Biol. 2014, 20, 3229–3237. [Google Scholar] [CrossRef] [PubMed]
- Wu, C.; Liang, N.; Sha, L.; Xu, X.; Zhang, Y.; Lu, H.; Song, L.; Song, Q.; Xie, Y. Heterotrophic respiration does not acclimate to continuous warming in a subtropical forest. Sci. Rep. 2016, 6, 21561. [Google Scholar] [CrossRef] [PubMed]
- Wythers, K.R.; Reich, P.B.; Tjoelker, M.G.; Bolstad, P.B. Foliar respiration acclimation to temperature and temperature variable q10 alter ecosystem carbon balance. Glob. Chang. Biol. 2005, 11, 435–449. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, T.; Huang, M.; Yao, Y.; Ciais, P.; Piao, S. Changes in interannual climate sensitivities of terrestrial carbon fluxes during the 21st century predicted by cmip5 earth system models. J. Geophys. Res. Biogeosci. 2016, 121, 903–918. [Google Scholar] [CrossRef]
- Su, H.; Feng, J.; Axmacher, J.C.; Sang, W. Asymmetric warming significantly affects net primary production, but not ecosystem carbon balances of forest and grassland ecosystems in northern China. Sci. Rep. 2015, 5, 9115. [Google Scholar] [CrossRef] [PubMed]
- Zhao, M.; Heinsch, F.A.; Nemani, R.R.; Running, S.W. Improvements of the MODIS terrestrial gross and net primary production global data set. Remote Sens. Environ. 2005, 95, 164–176. [Google Scholar] [CrossRef]









| Year | Period | a | b | c | d | e | R2 | p |
|---|---|---|---|---|---|---|---|---|
| 2009 | GS | 0.195 * | 2.631 ** | 0.044 ** | 1.691 | 9.551 | 0.56 | *** |
| NG | 0 | 2.009 *** | 0.044 *** | 1.828 | 14.714 | 0.78 | *** | |
| 2010 | GS | 0.293 ** | 6.436 *** | −0.012 * | 1.138 | −4.209 | 0.84 | *** |
| NG | 0 | 2.085 *** | 0.015 * | 6.569 | 53.088 | 0.17 | *** | |
| 2011 | GS | 0.517 *** | 2.712 * | −0.057 * | −0.449 | 55.408 | 0.71 | *** |
| NG | 0 | 1.058 *** | 0.061 ** | 5.655 | 45.792 | 0.30 | *** | |
| All | GS | 0.268 *** | 3.657 *** | 0.017 * | 1.875 * | 7.562 | 0.54 | *** |
| NG | 0 | 1.652 *** | 0.045 *** | 5.151 | 42.125 | 0.38 | *** |
| Method | Daily Average GPP Estimations (n = 21) (g C m−2 8 days−1) | Cumulative GPP Estimations (g C m−2 year−1, n = 3) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean (SD) | RMSE | RPE (%) | |||||||||||
| 2009 | 2010 | 2011 | 2009 | 2010 | 2011 | Mean | 2009 | 2010 | 2011 | Mean | Mean (SD) | RMSE | |
| MOD5 | 4.54 (3.26) *** | 6.09 (5.09) ** | 4.59 (3.32) *** | 3.85 | 4.88 | 4.65 | 4.46 | −39.7 | −30.5 | −47.44 | −39.2 | 106.55 (18.50) a | 69.92 |
| MOD | 7.02 (3.79) | 8.20 (4.05) | 7.51 (4.39) | 2.1 | 2.46 | 3.04 | 2.53 | −6.8 | −6.3 | −14.0 | −9.0 | 159.17 (12.51) bc | 17.43 |
| MODR | 8.55 (6.22) | 10.33 (7.51) | 10.15 (7.63) | 3.24 | 5.29 | 4.89 | 4.47 | 13.6 | 17.9 | 16.2 | 15.9 | 203.21 (20.55) d | 28.43 |
| VPM | 7.89 (3.13) | 8.16 (3.47) | 8.18 (3.17) | 2.11 | 2.57 | 2.70 | 2.46 | 4.7 | −6.8 | −6.3 | −2.8 | 169.63 (3.47) cd | 10.81 |
| PCM | 5.62 (5.56) * | 6.64 (6.05) * | 5.69 (4.86) *** | 3.57 | 4.88 | 3.95 | 4.13 | −25.4 | −24.2 | −34.9 | −28.2 | 125.61 (11.94) ab | 50.65 |
| AVM | 6.44 (4.89) | 7.24 (5.22) | 7.71 (5.87) | 2.72 | 3.53 | 2.70 | 2.98 | −14.4 | −17.4 | −11.7 | −14.5 | 149.75 (13.49) bc | 25.86 |
| EC | 7.53 (3.96) | 8.76 (3.84) | 8.74 (4.81) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 175.19 (14.81) cd | 0 |
| Period | Method * | Daily Re Estimations (g C m−2 8 days−1) | Cumulative Re Estimations (n = 3) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Mean (SD) | RMSE | Mean (SD) (g C m−2) | RMSE (g C m−2) | |||||||
| 2009 | 2010 | 2011 | 2009 | 2010 | 2011 | Mean | ||||
| GS (n = 21) | MODM | 6.90 (1.12) | 7.69 (1.47) | 6.71 (2.22) | 0.59 | 0.81 | 1.51 | 0.97 | 149.12 (10.83) a | 7.24 |
| VPMM | 6.90 (0.97) | 7.47 (1.50) | 5.91 (1.42) | 0.82 | 0.83 | 1.44 | 1.03 | 142.04 (13.60) a | 2.94 | |
| ECM | 6.90 (0.96) | 7.47 (1.56) | 6.16 (1.23) | 0.84 | 0.72 | 1.39 | 0.98 | 143.71 (13.90) a | 0.05 | |
| EC | 6.90 (1.27) | 7.47 (1.73) | 6.16 (2.56) | 0 | 0 | 0 | 0 | 143.74 (13.90) a | 0 | |
| NG (n = 25) | Model | 2.63 (0.89) | 2.23 (0.19) | 1.33 (0.41) | 0.44 | 0.80 | 0.71 | 0.65 | 51.49 (16.66) A | 0.16 |
| EC | 2.62 (0.75) | 2.23 (0.84) | 1.32 (0.85) | 0 | 0 | 0 | 0 | 51.36 (16.72) A | 0 | |
| Site | Method | Year | Ra/Re (1 − β*γ) | References |
|---|---|---|---|---|
| Alpine meadow, Tibet | Regression | 2011 | 0.20–0.91 | [45] |
| Alpine meadow, Qinghai | Plant exclusion | 2003 | 0.39–0.46 | [83] |
| Alpine meadow, Haibei | Regression | 2009 | 0.53–0.80 | [79] |
| Alpine meadow, Tibet | Satellite-based | 2009–2011 | 0.27–0.56 | This study |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Niu, B.; He, Y.; Zhang, X.; Zong, N.; Fu, G.; Shi, P.; Zhang, Y.; Du, M.; Zhang, J. Satellite-Based Inversion and Field Validation of Autotrophic and Heterotrophic Respiration in an Alpine Meadow on the Tibetan Plateau. Remote Sens. 2017, 9, 615. https://doi.org/10.3390/rs9060615
Niu B, He Y, Zhang X, Zong N, Fu G, Shi P, Zhang Y, Du M, Zhang J. Satellite-Based Inversion and Field Validation of Autotrophic and Heterotrophic Respiration in an Alpine Meadow on the Tibetan Plateau. Remote Sensing. 2017; 9(6):615. https://doi.org/10.3390/rs9060615
Chicago/Turabian StyleNiu, Ben, Yongtao He, Xianzhou Zhang, Ning Zong, Gang Fu, Peili Shi, Yangjian Zhang, Mingyuan Du, and Jing Zhang. 2017. "Satellite-Based Inversion and Field Validation of Autotrophic and Heterotrophic Respiration in an Alpine Meadow on the Tibetan Plateau" Remote Sensing 9, no. 6: 615. https://doi.org/10.3390/rs9060615
APA StyleNiu, B., He, Y., Zhang, X., Zong, N., Fu, G., Shi, P., Zhang, Y., Du, M., & Zhang, J. (2017). Satellite-Based Inversion and Field Validation of Autotrophic and Heterotrophic Respiration in an Alpine Meadow on the Tibetan Plateau. Remote Sensing, 9(6), 615. https://doi.org/10.3390/rs9060615