1. Introduction
Increasing demand for accurate sea level anomaly (SLA) data close to the coast has led to a huge development in coastal altimetry and its applications, such as coastal management, long-term monitoring of coastal dynamics and storm surge studies.
Satellite radar altimeters measure the range, a distance between satellite and the nadir surface, by retrieving the two-way travel time of radar short pulses sent to and reflected from the ocean surface. The SLA is referenced to a mean sea surface and can be then derived from the range and satellite orbit. The reflected signal is called the ‘waveform’ and represents the time evolution of the reflected power as the radar signal hits the surface. Waveforms over a homogeneous ocean surface (e.g., open ocean without land interference) can generally be described by Brown [
1] model. It features a sharp leading edge up to the maximum value of the amplitude, followed by a gently sloping plateau known as the trailing edge.
In the proximity of land, conventional Ku-band altimetry data usually requires a complex sequence of processing steps to get usable information about the SLAs. This is because the waveform signals are contaminated by land or calm waters (cf. [
2,
3]) and the corrections are less accurate over the coastal regime. Through processing, better estimates of the range parameter (that is related to the SLA), and the geophysical corrections (particularly the wet tropospheric, dynamic atmospheric and ocean tide corrections) can be obtained. The range estimates can be optimised through a ground re-processing protocol called ‘waveform retracking’ (cf. [
4,
5,
6,
7,
8,
9,
10,
11]), which was routinely conducted over global oceans to improve the accuracy of altimetry measurements. The state-of-the-art about retracking and geophysical corrections can be found in the book
Coastal Altimetry by Vignudelli et al. [
12], and in particular in the chapter by Gommenginger et al. [
13] and Andersen and Scharroo [
14].
In recent years, many initiatives were undertaken to provide data upgrades (e.g., PISTACH and PEACHI products) and new retracking strategies over coastal regions (e.g., [
8,
15,
16,
17,
18,
19,
20,
21]). As a result, the altimetry no-data gap was reduced to ~10 km to the coastline. However, within ~10 km from the coastline, the improvement of altimetry data is still challenging due to the complex nature of coastal topography and calm sea states.
When attempting to extract precise sea levels from corrupted waveforms near shore, several researchers (cf. [
5,
22,
23]) suggest combining multiple retracking algorithms for dealing with various waveform shapes. However, there is a lack of clear recommendations and guidelines on which retracker should be used under various conditions (cf. [
24]). Several methods were proposed regarding the selection of the optimal retracker for reprocessing various waveform patterns. The rule-based expert system was found useful for proposing dedicated retrackers based on waveform characteristics [
5,
23]. Because the system is mainly based on physical features of waveforms, it is crucial to accurately classify altimetric waveforms into different classes, so that they can be assigned to corresponding retrackers. It is also important to minimise the discontinuity of the retrieved geophysical parameters when switching retrackers from the open ocean to the coast, or vice versa. One cannot simply switch from one retracker to another due to the relative sea level offsets between them (cf. [
8,
25,
26]).
In this study, we initiate a novel method to retrieve precise SLAs from multiple retracking solutions through a Coastal Altimetry Waveform Retracking Expert System (CAWRES). The CAWRES is designed to optimise the estimation of SLAs by selecting the optimal retracker via a fuzzy expert system and to provide a seamless transition from the open ocean to coastlines (or vice versa) when switching retrackers via a neural network approach. The parameter of interest is the SLA that refers to the mean sea surface rather than the geoid because the geoid is inaccurate at high frequency wavelengths [
27].
The article is organised as follows: the study area and data are described in
Section 2; the development of the CAWRES is described in
Section 3; the consideration and initial testing of CAWRES is discussed in
Section 4; the performance of CAWRES in the region of the Great Barrier Reef in Australia, against geoid height and tide gauge is provided in
Section 5; and conclusions and recommendations are provided in
Section 6.
2. Study Area and Data
The region of the Great Barrier Reef in Australia (
Figure 1) is chosen as the study area due to it’s unique morphology characterised by distinct basins, and sub-basins surrounded by a complex shoreline with specific oceanographic features. Situated in the Coral Sea off the coast of Queensland, the Great Barrier Reef is the world’s largest reef system. It is ~2600 km in length and is composed of ~3000 individual reefs and ~900 islands. It experiences a tropical climate with a severe tropical cyclone season during the austral summer. Data selected in this area can capture diverse waveform patterns due to the spatial complexity of the topography and the temporal variability of coastal sea states.
The data used are Jason-1 and Jason-2/OSTM obtained during the tandem mission. The Ku-band 20-Hz 104-sample waveform data are from January 2009 to December 2011, which corresponds to cycles 262 to 370 of Jason-1 and cycles 19 to 143 of Jason-2. Over the Great Barrier Reef, waveforms along five ascending passes (73, 99, 149, 175, and 251) and four descending passes (36, 112, 188, and 214) of both satellites are investigated (
Figure 1).
In producing SLAs, environmental and geophysical corrections from Sensor Geophysical Data Record (SGDR) products and the mean sea surface from DTU10 model [
28] are applied to the altimeter range. The wet and dry tropospheric corrections are from the European Centre for Medium-Range Weather Forecasts (ECMWF) numerical prediction models, and ionospheric correction is from the General Ionospheric Model Map. The more accurate instrumental radiometer wet correction and dual frequency ionospheric correction are not used because of coastal contamination effects. The ocean tidal signals are removed using a pointwise tide modelling [
17] rather than the global ocean tide model, such as FES2004 and GOT4.8, because it better resolves the tidal signals in the study region. The sea state bias correction is not applied because it is not appropriate for waveforms near coasts (cf. [
14]). It is applied neither to coastal data to avoid additional error nor to open ocean data to keep consistency of datasets in the area. The corrections were interpolated from 1 Hz to 20 Hz.
The quality and consistency of sea levels derived from CAWRES is compared with geoid height and tide gauges. The geoidal height is based on the Earth Gravitational Model 2008 (EGM2008) with 2.5 min resolution. The tide gauge data are from the University of Hawaii Sea Level Center). It is the hourly sea level data from Townsville (19.25°S, 146.83°E), Bundaberg (24.75°S, 152.42°E), and Honiara (9.44°S, 159.95°E) stations (see
Figure 1). The assessment with tide gauge merits to finding both the accuracy and precision of the SLA estimates, while with the geoidal heights, only the precision can be computed.
3. The Development of CAWRES
The CAWRES consists of two major principles. The first is to minimise the relative offset in the retrieved SLAs when switching from one retracker to another using a neural network (
Section 4.1.2). The second is to reprocess altimeter waveforms using the optimal retracker based on the analysis from a fuzzy expert system. The CAWRES employs multiple retracking algorithms to reprocess various waveforms near a shore. They are the Brown [
1] physical-based retrackers that retrack the full-waveform (cf. [
5]) (hereafter called the ‘Ocean Model’ retracker) and sub-waveform (cf. [
8]) (hereafter called the ‘Sub-waveform’ retracker), and the modified threshold empirical-based retrackers (cf. [
18]) with 10%, 20% and 30% of threshold levels (hereafter called the ‘modthreshold10’, ‘modthreshold20’ and ‘modthreshold30’). These retrackers are prioritised depending on the waveforms shape to optimise the SLA estimation. The system repeatedly retracks waveforms until it finds the optimal retracker based on the analysis from the fuzzy expert system. A retracker is considered as optimal when it produces the highest quality retracked SLAs. Detailed information is provided in
Section 3.1.
Unlike other retracking expert systems [
5,
23] that consider only the information about the physical features (i.e., shapes) of waveforms, CAWRES considers both the shapes of waveforms and the statistical features of retracking results to select the optimal retracker. Thus, CAWRES reduces the risk of assigning the waveform to an inappropriate retracker when the classification procedure is unable to accurately identify the class of corrupted waveforms near coasts. The fuzzy system is used because of its capability to model the ambiguousness that occurs during the evaluation process, which cannot be properly described by the classical decision system (e.g., rule-based expert system) [
29].
When employing multiple retracking algorithms to improve the estimation of the SLAs in coastal regions, the major problem is that ‘jumps’ may appear in the retracked SLA profiles due to the presence of relative offsets among various retrackers [
5,
8,
19,
22,
26]. An analysis is reported in
Section 4.1.1 to understand the behaviour of the offset among various retrackers. To reduce the offset in retracked SLAs, the novel ideas that exploit a neural network approach are explored because it performs a comprehensive analysis to recognise complex patterns between various retrackers.
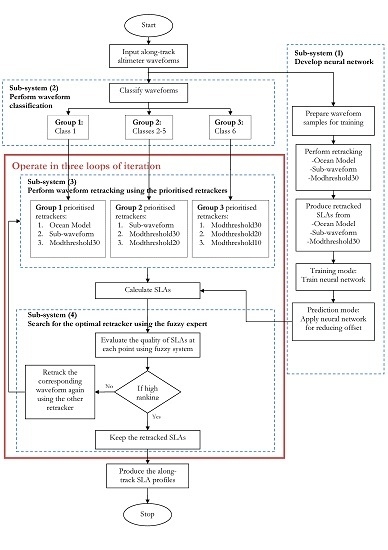
Figure 2 shows the block diagram of the CAWRES. The system consists of four major sub-systems:
For each satellite track, for example Jason-2 cycle 19 pass 214, the system starts with sub-system (1) by selecting waveform samples and performs the training mode operation in the neural network. The outputs from sub-system (1) are the trained neural network to determine offset 1 (hereafter called the ‘NN1’) and offset 2 (hereafter called the ‘NN2’), which are used later in sub-system (3) to minimise the offsets. The offset 1 is computed between full-waveform and modthreshold30 retrackers and offset 2 is between sub-waveform and modthreshold30 retrackers. These outputs are produced for each individual satellite cycle and pass. It is noted that the offsets between modthreshold30 and modthreshold20 (modthreshold10) retrackers are not computed because our initial study found that the values are insignificant (<5 cm).
In sub-system (2), all waveforms are classified into three groups that are retracked using corresponding retrackers. In sub-systems (3) and (4), the operations are performed in a loop of iterations. The waveform retracking is performed iteratively, from which waveforms in each group are retracked by the n prioritised retrackers where n = 1, 2, 3. A high priority is given to the physical-based retrackers (i.e., Ocean Model and sub-waveform) to reprocess Brown-like waveforms (group 1) and coastal waveforms (group 2) with clear leading edges because they can optimise the geophysical parameters based on a functional form of the reflecting surfaces. The statistical-based retracker is assigned to coastal waveforms (group 3), which appear to have no Brown-like leading edge and contains perturbations in their leading edge. The maximum iteration is three relative to the number of retracking algorithms used in each group.
At the first iteration (
n = 1), in sub-system (3), waveforms corresponding to group 1 are retracked by the full-waveform, whereas waveforms corresponding to groups 2 and 3 are retracked by the sub-waveform and modthreshold30 retrackers, respectively. This then produces an along-track retracked SLA profile. To minimise the relative offset among retrackers, NN1 and NN2 from sub-system (1) are used. NN1 is applied to the group that is retracked by the full-waveform, and NN2 is applied to the group that is retracked by the sub-waveform retracker (see
Section 4.1.2 for details on NN1 and NN2).
In sub-system (4), the retracked SLAs at each along-track point are subsequently analysed using the fuzzy expert system to quantify the quality of the retracked SLAs (see
Section 3.1 for detailed description). When the fuzzy system assesses the quality of the retracked SLA at a point as being high, it keeps the result to produce the final SLA profiles. When its quality is low, the corresponding waveform is retracked again (in sub-system 3) at the second iteration (
n = 2), using the second prioritised retracker: sub-waveform for group 1, modthreshold30 and modthreshold20 for groups 2 and 3, respectively. The NN2 is subsequently applied to a point that is retracked by the sub-waveform retracker to realign them to the modthreshold30 retracked SLAs. The quality of retracked SLAs is then assessed again using the fuzzy system in sub-system (4). When the quality is found to be low, the waveform is retracked again at the third iteration (
n = 3) using the third prioritised retracker: modthreshold30, modthreshold20 and modthreshold10 for groups 1, 2 and 3, respectively. Retracked SLAs with high quality are kept for the final SLA profiles. However, if no high quality retracked SLA is found at a point after the third iteration, the retracked SLA corresponding to the highest quality retracker is used as the final output of SLAs.
After retracking, the range correction is computed, and subsequently is applied to the altimetry observed range to produce the retracked range. The retracked SLA is computed by subtracting the retracked range from the satellite orbital height, geophysical corrections (e.g., tides, wet and dry tropospheric and ionospheric) and mean sea surface. For the tidal correction, the pointwise tide modelling [
31] is applied rather than the global ocean tide models (e.g., GOT 4.8, FES2004 and DTU10) to better remove the shallow water tides (cf. [
17]).
Considering that the system in
Figure 2 involves complex computations, we examine the execution times of CAWRES using MATLAB implementation for one cycle along different passes (
Table 1). It is processed using a 2.20 GHz i5 CPU, 8 GB Random Access Memory (RAM) and Intel High Definition Graphics 5300. Results shown in
Table 1 indicate that the computational time of CAWRES to process a bunch (between 2211 and 6099) of waveforms is ≤306 s with the averaged execution time for an altimetric waveform is ~0.05 s. This is considered reasonable for such a complex system. Note that the implementation of CAWRES in MATLAB has considered several techniques to accelerate the execution times, including the pre-allocation memory and parallel iterations.
Fuzzy Expert System
This section describes about the fuzzy expert system that is applied in subsystem (4) of CAWRES. It is used to evaluate the quality of retracked SLAs because of its capability for integrating information about the statistical features of retracking results, and determining the quality of retracked SLAs accordingly.
After waveform retracking in subsystem (3), the quality of retracking results is computed using a fuzzy expert system. The input variables included in the fuzzy expert system are: (1) the difference of the retracked SLAs from the mean sea surface (Dif_ssh); (2) the differences between two successive retracked SLAs (Dif_ssh_prev1); (3) the difference between a retracked SLAs and the retracked SLA after next (Dif_ssh_prev2); and (4) for the fitting functions of the full-waveform and sub-waveform models, the goodness of fit (r2), which is determined by the correlation level between waveform samples and fitted values, is included. Dif_ssh_prev1 and Dif_ssh_prev2 are included in the system to ensure that the optimal retracker is the one that yields small differences between the previous SLAs. This is because the SLA generally varies smoothly within a certain distance across the ocean surface.
Based on fuzzy logic, the variables can be represented as a set of mathematical principles for knowledge representation based on degrees of membership and degrees of truth. The range of values of a variable represents the universe discourse of that variable. For example, the universe discourse of the linguistic variable r2 might have a range between 0 and 1, and may include such fuzzy subsets as poor and good.
Figure 3 shows examples of the fuzzy set of
r2 and
Dif_ssh_prev1. The
x-axis represents the universe of discourse, which shows the range of all possible values applicable to the variables
r2 and
Dif_ssh_prev1. The
y-axis represents the membership value of the fuzzy set for both variables. The universe of discourse
r2 consists of two fuzzy sets, poor and good, and the universe of discourse
Dif_ssh, Dif_ssh_prev1 and
Dif_ssh_prev2 consists of two fuzzy sets, small and large. The characteristics of these fuzzy sets are shown in
Table 2.
Based on the input variables, the system evaluates the quality of retracking results by giving the rank value (between 0 and 10). The rank values between 8 and 10, and 0–7 are of high and low quality, respectively. The evaluation process considers 13 rules. For example,
If r2 is good, and Dif_ssh, Dif_ssh_prev1 and Dif_ssh_prev2 are small, then ranking = high
If r2 is poor, and Dif_ssh, Dif_ssh_prev1 and Dif_ssh_prev2 are large, then ranking = low
If r2 is good, and Dif_ssh, Dif_ssh_prev1 and Dif_ssh_prev2 are large, then ranking = low
If r2 is none, and Dif_ssh, Dif_ssh_prev1 and Dif_ssh_prev2 are large, then ranking = low
If r2 is none, and Dif_ssh, Dif_ssh_prev1 and Dif_ssh_prev2 are small, then ranking = high
The analysis provided by the fuzzy system is used as a basis for determining the optimal retracker near coasts. When it considers the quality of retracked SLA as ‘high ranking’ (value between 8 and 10), the system keeps the retracked SLA, which will be used to produce the final SLA profile. In the case of ‘low ranking’ (value between 0 and 7), the waveform is retracked iteratively using the other retrackers, based on their priority, until a retracked SLA with a ‘high ranking’ is found. If a ‘high ranking’ retracked SLA is not found after all the three retrackers related to the waveform group were applied, the retracked SLA corresponding to the highest ranking retracker is used as the output of the SLA profile.
Figure 4 shows an example of retracked SLA profiles (top) and their ranking values (bottom) during iterations 1 to 3. Red circles show problematic areas, where ‘low ranking’ retracked SLAs are found. These areas are iteratively retracked until the optimal retracker is found, which is indicated by the ‘high ranking’ value. In this example, the SLA profile during iteration 1 is found to fluctuate with a standard deviation of 166 cm. However, during iteration 3, the standard deviation reduces to 95 cm. This indicates the fuzzy expert system enhances the SLA precision by proposing the optimal retracker to reprocess waveforms.
6. Conclusions and Recommendations
The CAWRES was developed to optimise the SLA estimation from Jason coastal waveforms. The novel idea of the system is (1) to reprocess altimeter waveforms using the optimal retracker, which is sought based on the analysis from a fuzzy expert system; and (2) to provide a seamless transition of retracked SLAs when switching from one retracker to another, based on the analysis from a neural network. With the CAWRES, the risk of assigning the waveform to an inappropriate retracker is minimised by including information about the waveform shapes and statistical features of the retracking results in the fuzzy expert system. It also reduces inconsistency in the retracked SLAs when switching retrackers by employing the neural network to handle the nonlinear relationship between the retracker and the scattering surface, thus providing seamless transition from the open ocean to coast, and vice versa.
The results over the tested regions emphasise that the retracked sea levels from the CAWRES are consistent with those of the geoid height and tide gauges. It reduces the STD of the MLE4 retracked sea levels by up to 63 cm for Jason-1 and 100 cm for Jason-2. It recovers up to 16% more data than the MLE4 retrackers over the region. Although CAWRES improves the retracking solution over the region, sometimes, the quality of the retrieved SLAs is poor. Therefore, the CAWRES products should be used with caution. Analysis with tide gauges indicates that SLAs from the CAWRES are more reliable than those of from the SGDR products, in the sense that it has a higher (≥0.77) temporal correlation and smaller (≤19 cm) RMS errors. These values indicate that the CAWRES produces more precise and accurate SLAs than those of other retrackers.
The results demonstrated that the CAWRES has the potential of being applied to coastal regions elsewhere, as well as other satellite altimeter waveforms. However, this requires extensive validation activities with various sources of in situ datasets such as high frequency radar and Argo floats. The experimental region has also to be extended to other locations to quantify the performance of CAWRES over different coastal characteristics.
It is expected that the long-term SLA time series can be extended near the coast through retracking waveforms using the CAWRES once new and near future radar altimetry missions start to offer better observation coverage in the coastal zone. However, further development of the coastal waveform retracking method is still required because the current retracking algorithms cannot recover the highly corrupted waveforms when the ground track is much closer to the coastline than what was achieved so far. Further work is needed on the improvement of the existing retracking models by including the effect of land on the altimeter waveforms, or the development of new models by including the scattering from non-linear surfaces to better fit the corrupted waveforms near coasts. In addition, further analysis on the assessment of the offset between various retrackers is needed. This study identified that the offset between the retrackers varies depending on the variation of SWH. Further research is essential regarding the use of the neural network for reducing the offset in the retracked SLAs. The results also show that the error in the SSHs with respect to geoid can reach decade centimetres, which may be due to the existence of the offset value between modthreshold30 and modthreshold20 (modthreshold10) retrackers. Future research should consider the value of offset between those retrackers to improve the accuracy of SSHs.
Studies are currently in progress to examine the applicability of the CAWRES to the other satellite altimeter waveforms, particularly the Sentinel-2 that is equipped with advanced technology of altimetry. In addition, comparison of results with other independent in situ data such as the coastal high frequency radar and Regional Ocean Modelling System is also under further validation.