Optimizing Semi-Analytical Algorithms for Estimating Chlorophyll-a and Phycocyanin Concentrations in Inland Waters in Korea
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Site
2.2. Field Monitoring and Experiment
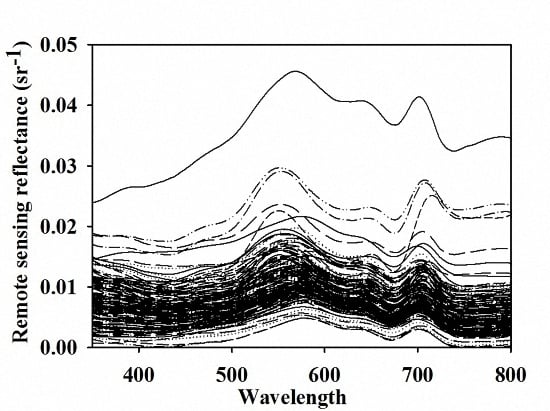
2.2.1. Remote Sensing Reflectance Retrieval
2.2.2. Extraction of Chl-a and PC
2.2.3. Absorption Coefficient Analysis of Phytoplankton
2.3. Semi-Analytical Algorithms for Inland Water
2.4. Global Sensitivity Analysis
2.5. Parameter Optimization
3. Results
3.1. Temporal Variability of Chl-a and PC
3.2. Sensitivity of Parameters in Semi-Analytical Algorithms
3.3. Optimization Results
3.3.1. Estimation of the Absorption Coefficient
3.3.2. Performance of Semi-Analytical Algorithms
4. Discussion
5. Conclusions
- The most sensitive parameters were the specific absorption coefficient and the parameters of the Y function in both Chl-a and PC algorithms.
- Wavelengths around 620 nm were selected for calculating backscattering, and the Y function became a relatively higher value than the earlier published one. This showed that the Baekje reservoir had relatively high absorptive water near the surface.
- The multi-objective optimization improved the performance of estimating the Chl-a and PC concentrations when compared with the estimates obtained from earlier published parameters and single-objective optimization results.
- The multi-objective optimization was more significant when considering both the absorption coefficient and biomass concentration compared to the single-objective optimization.
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Ju, H.J.; Choi, I.C.; Yoon, J.H.; Lee, J.J.; Lim, B.J.; Lee, S.H. Analysis of cyanobacteria broth pattern in Bekjae weir during recent 3 years. In Proceedings of the Korean Society on Water Environment & Korean Society of Water & Wastewater conference, Seoul, Korea, 27 October 2016; pp. 562–563. [Google Scholar]
- Boyer, J.N.; Kelble, C.R.; Ortner, P.B.; Rudnick, D.T. Phytoplankton bloom status: Chlorophyll-a biomass as an indicator of water quality condition in the southern estuaries of Florida, USA. Ecol. Indic. 2009, 9, 56–67. [Google Scholar] [CrossRef]
- Carpenter, S.R.; Cole, J.J.; Pace, M.L.; Batt, R.; Brock, W.A.; Cline, T.; Coloso, J.; Hodgson, J.R.; Kitchell, J.F.; Seekell, D.A.; et al. Early warnings of regime shifts: A whole-ecosystem experiment. Science 2011, 332, 1079–1082. [Google Scholar] [CrossRef] [PubMed]
- Kudela, R.M.; Palacios, S.L.; Austerberry, D.C.; Accorsi, E.K.; Guild, L.S.; Torres-Perez, J. Application of hyperspectral remote sensing to cyanobacterial blooms in inland waters. Remote Sens. Environ. 2015, 167, 196–205. [Google Scholar] [CrossRef]
- Duan, H.; Ma, R.; Hu, C. Evaluation of remote sensing algorithms for cyanobacteria pigment retrievals during spring bloom formation in several lakes of East China. Remote Sens. Environ. 2012, 126, 126–135. [Google Scholar] [CrossRef]
- Gilerson, A.A.; Gitelson, A.A.; Gurlin, D.; Moses, W.; Ioannou, I.; Ahmed, S. Algorithms for remote estimation of chlorophyll-a in coastal and inland waters using red and near infrared bands. Opt. Express 2010, 18, 24109–24125. [Google Scholar] [CrossRef] [PubMed]
- Gitelson, A.; Mayo, M.; Yacobi, Y.Z. Signature analysis of reflectance spectra and its application for remote observations of the phytoplankton distribution in Lake Kinneret. Measures Physiques et Signatures en Teledetection. In Proceedings of the ISPRS 6th International Symposium, Val d’Isere, France, 17–21 January 1994; pp. 277–283. [Google Scholar]
- Gons, H.J. Optical teledetection of chlorophyll a in turbid inland waters. Environ. Sci. Technol. 1999, 33, 1127–1132. [Google Scholar] [CrossRef]
- Li, L.; Li, L.; Song, K.; Li, Y.; Tedesco, L.P.; Shi, K.; Li, Z. An inversion model for deriving inherent optical properties of inland waters: Establishment, validation and application. Remote Sens. Environ. 2013, 135, 150–166. [Google Scholar] [CrossRef]
- Randolph, K.; Wilson, J.; Tedesco, L.; Li, L.; Pascual, D.L.; Soyeux, E. Hyperspectral remote sensing of cyanobacteria in turbid productive water using optically active pigments, chlorophyll-a and phycocyanin. Remote Sens. Environ. 2008, 112, 4009–4019. [Google Scholar] [CrossRef]
- Ritchie, R.J. Universal chlorophyll equations for estimating chlorophylls a, b, c, and d and total chlorophylls in natural assemblages of photosynthetic organisms using acetone, methanol, or ethanol solvents. Photosynthetica 2008, 46, 115–126. [Google Scholar] [CrossRef]
- Simis, G.H.; Peters, W.M.; Gons, H.J. Remote sensing of the cyanobacterial pigment phycocyanin in turbid inland water. Limnol. Oceanogr. 2005, 50, 237–245. [Google Scholar] [CrossRef]
- Simis, G.H.; Ruiz-Verdu, A.; Gominguez-Gomez, J.A.; Pena-Martinez, R.; Peter, W.M.; Gons, H.M. Influence of phytoplankton pigment composition on remote sensing of cyanobacterial biomass. Remote Sens. Environ. 2007, 106, 414–427. [Google Scholar] [CrossRef]
- Li, L.; Li, L.; Song, K. Remote sensing of freshwater cyanobacteria: An extended IOP inversion model of inland waters (IIMIW) for partitioning absorption coefficient and estimating phycocyanin. Remote Sens. Environ. 2015, 157, 9–23. [Google Scholar] [CrossRef]
- Ogashawara, I.; Mishra, D.R.; Mishra, S.; Curtarelli, M.P.; Stech, J.L. A performance review of reflectance based algorithms for predicting phycocyanin concentrations in inland waters. Remote Sens. 2013, 5, 4774–4798. [Google Scholar] [CrossRef]
- Le, F.C.; Li, Y.M.; Zha, Y.; Sun, D.Y.; Yin, B. Validation of a quasi-analytical algorithm for highly turbid eutrophic water of Meiliang bay in Taihu lake, China. IEEE Trans. Geosci. Remote Sens. 2009, 47, 2492–2500. [Google Scholar]
- Le, C.; Li, Y.; Zha, Y.; Sun, D.; Huang, C.; Zhang, H. Remote estimation of chlorophyll a in optically complex waters based on optical classification. Remote Sens. Environ. 2011, 115, 725–737. [Google Scholar] [CrossRef]
- Ministry of Environment. Nonpoint Source Management Comprehensive Plan of Geum River; Report1-23; Ministry of Environment: Daejeon, Korea, 2015.
- Kim, Y.H.; Lee, E.H.; Kim, K.H.; Kim, S.H. Analysis of exclusive causality between environment factors and cell number of cyanobacteria in Guem river. J. Environ. Sci. Int. 2016, 25, 937–950. [Google Scholar] [CrossRef]
- American Public Health Association (APHA). Standard Methods for the Examination of Waterand Waste Water, 21st ed.; APHA-AWWA-WPCF: Washington, DC, USA, 2001. [Google Scholar]
- Pyo, J.C.; Ha, S.H.; Pachepsky, Y.A.; Lee, H.; Ha, L.; Nam, G.B.; Kim, M.S.; Im, J.H.; Cho, K.H. Chlorophyll-a concentration estimation using three difference bio-optical algorithms, including a correction for the low concentration range: The case of the Yiam reservoir, Korea. Remote Sens. Lett. 2016, 7, 407–416. [Google Scholar] [CrossRef]
- Bennett, A.; Bogorad, L. Complementary chromatic adaptation in a filamentous blue-green alga. J. Cell Biol. 1973, 58, 419–435. [Google Scholar] [CrossRef] [PubMed]
- Sarada, R.; Pillai, M.G.; Ravishankar, G.A. Phycocyanin from Spirulina sp: Influence of processing of biomasson phycocyanin yield, analysis of efficacy of extraction methods and stability studies on phycocyanin. Process Biochem. 1999, 34, 795–801. [Google Scholar] [CrossRef]
- Tassan, S.; Ferrari, G.M. An alternative approach to absorption measurements of aquatic particles retained on filters. Limnol. Oceanogr. 1995, 40, 1358–1368. [Google Scholar] [CrossRef]
- Mueller, J.L.; Fargion, G.S.; McClain, C.R. Inherent Optical Properties: Instruments, Characterization, Field Measurements and Data Analysis Protocols. Ocean Optics Protocols for Satellite Ocean Color Sensor Validation; Revision 4; Volume IV; National Aeronautics and Space Administration: Greenbelt, MD, USA, 2003.
- Gons, H.J.; Auer, M.T.; Effler, S.W. MERIS satellite chlorophyll mapping of oligotrophic and eutrophic waters in the Laurentian Great Lakes. Remote Sens. Environ. 2008, 112, 4098–4106. [Google Scholar] [CrossRef]
- Buiteveld, H.; Hakvoort, J.H.M.; Donze, M. The optical properties of pure water. SPIE Proc. Ocean Opt. XII 1994, 2258, 174–183. [Google Scholar]
- Santiago-Santos, M.C.; Ponce-Noyolam, T.; Olvera-Ramirez, R.; Ortega-Lopez, J.; Canizares-Villanueva, R.O. Extraction and purification of phycocyanin from Calothrix sp. Process Biochem. 2008, 37, 2047–2052. [Google Scholar] [CrossRef]
- Gons, H.J.; Rijkeboer, M.; Ruddick, K.G. Effect of a waveband shift onchlorophyll retrieval from MERIS imagery of inland and coastal waters. J. Plankton Res. 2005, 27, 125–127. [Google Scholar] [CrossRef]
- Morris, M.D. Factorial sampling plans for preliminary computational experiments. Technometrics 1991, 33, 161–174. [Google Scholar] [CrossRef]
- Pianosi, F.; Sarrazin, F.; Wagener, T. A matlab toolbox for global sensitivity analysis. Environ. Model. Softw. 2015, 70, 80–85. [Google Scholar] [CrossRef]
- Campolongo, F.; Cariboni, J.; Saltelli, A.; Schoutens, W. Enhancing the Morris method. In Sensitivity Analysis of Model Output; Los Alamos National Laboratory: Los Alamos, NM, USA, 2005. [Google Scholar]
- Ekstrom, P.A.; Broed, R. Sensitivity Analysis Methods and a Biosphere Test Case Implemented in EIKOS; Working Report 2006-31; Olkiluoto: Eurajoki, Finland, 2006. [Google Scholar]
- Neter, J.; Wasserman, W. Applied Linear Statistical Models: Regression, Analysis of Variance, and Experimental Designs, 4th ed.; WCB/McGraw-Hill: Columbus, OH, USA, 1974. [Google Scholar]
- Duong, T.T.; Le, T.P.Q.; Dao, T.S.; Pflugmacher, S.; Newall-Rochelle, E.; Hoang, T.K.; Vu, T.N.; Ho, C.T.; Dang, D.K. Seasonal variation of cyanobacteria and microcystins in the Nui Coc Reservoir, Northern Vietnam. J. Appl. Phycol. 2013, 25, 1065–1075. [Google Scholar] [CrossRef]
- Aurin, D.A.; Dierssen, H.M. Advantages and limitations of ocean color remotesensing in CDOM-dominated, mineral-rich coastal and estuarine waters. Remote Sens. Environ. 2012, 125, 181–197. [Google Scholar] [CrossRef]
- Lee, Z.P.; Carder, K.L.; Arnone, R.A. Deriving inherent optical properties from water color: A multiband quasi-analytical algorithm for optically deep waters. Appl. Opt. 2002, 41, 5755–5772. [Google Scholar] [CrossRef] [PubMed]
- Lee, Z.; Arnone, R.; Hu, C.; Werdell, P.J.; Lubac, B. Uncertainties of optical parameters and their propagations in an analytical ocean color inversion algorithm. Appl. Opt. 2010, 49, 369–381. [Google Scholar] [CrossRef] [PubMed]
- Smith, R.C.; Baker, K.S. Optical properties of the clearest natural water (200–800 nm). Appl. Opt. 1981, 20, 177–184. [Google Scholar] [CrossRef] [PubMed]
- Ciotti, A.M.; Bricaud, A. Retrievals of a size parameter for phytoplankton and spectral light absorption by colored detrital matter from water-leaving radiances at SeaWiFS channels in a continental shelf region off Brazil. Limnol. Oceanogr. Methods 2006, 4, 237–253. [Google Scholar] [CrossRef]
- Wang, G.F.; Cao, W.X.; Yang, D.T.; Zhao, J. Decomposing total suspended particle absorption based on the spectral correlation relationship. Spectrosc. Spectr. Anal. 2009, 29, 201–206. [Google Scholar]
- Lee, Z.P.; Carder, K.L.; Mobley, C.D.; Steward, R.G.; Patch, J.S. Hyperspectral remote sensing for shallow waters: 2. Deriving bottom depths and water properties by optimization. Appl. Opt. 1999, 38, 3831–3843. [Google Scholar] [CrossRef] [PubMed]
- Gallegos, C.L.; Jordan, T.E.; Hines, A.H.; Weller, D.E. Temporal variability ofoptical properties in a shallow, eutrophic estuary: Seasonal and interannual variability. Estuar. Coast. Shelf Sci. 2005, 64, 156–170. [Google Scholar] [CrossRef]
- Gieskes, W.W.; Kraay, G.W. Unknown chlorophyll a derivatives in the North Sea and the tropical Atlantic Ocean revealed by HPLC analysis. Limnol. Oceanogr. 1983, 28, 757–766. [Google Scholar] [CrossRef]
- Inskeep, W.P.; Bloom, P.R. Extinction coefficients of chlorophyll-a and b in N,N-Dimethylformamide and 80% acetone. Plant Physiol. 1985, 77, 483–485. [Google Scholar] [CrossRef] [PubMed]
- Gitelson, A. The nature of the peak near 700 nm on the radiance spectra and its application for remoteestimation of phytoplankton pigments in inland waters. In Proceedings of the SPIE 1971 Optical Engineering and Remote Sensing, Bellingham, WA, USA, 13 August 1993; pp. 170–179. [Google Scholar]
- Schalles, J.F.; Gitelson, A.; Yacobi, Y.Z.; Kroenke, A.E. Chlorophyll estimation using whole seasonal, remotely sensed high spectral-resolution data for an eutrophic lake. J. Phycol. 1998, 34, 383–390. [Google Scholar] [CrossRef]
- Yacobi, Y.Z.; Gitelson, A.; Mayo, M. Remote sensing of chlorophyll in Lake Kinneret using high spectralresolution radiometer and Landsat TM: Spectral features of reflectance and algorithm development. J. Plankton Res. 1995, 17, 2155–2173. [Google Scholar] [CrossRef]


| Mean | Max. † | Min. † | Mean | Max | Min | |
|---|---|---|---|---|---|---|
| Chl-a (mg m−3) | PC (mg m−3) | |||||
| 06.10.2016 | 39.27 ± 7.48 ‡ | 52.86 | 24.89 | 0.18 ± 0.11 | 0.45 | 0 |
| 08.05.2016 | 36.49 ± 15.80 | 66.18 | 14.19 | 29.64 ± 24.16 | 104.28 | 6.25 |
| 08.12.2016 | 92.34 ± 51.91 | 243.14 | 33.94 | 169.72 ± 235.61 | 1014.35 | 32.63 |
| 08.19.2016 | 37.24 ± 8.02 | 61.44 | 25.95 | 38.07 ± 23.58 | 100.00 | 12.25 |
| 08.24.2016 | 32.06 ± 11.27 | 50.01 | 14.75 | 17.16 ± 24.84 | 95.28 | 1.96 |
| 09.06.2016 | 25.51 ± 11.32 | 60.88 | 11.85 | 1.23 ± 0.27 | 1.64 | 0.83 |
| 09.26.2016 | 29.12 ± 11.35 | 58.26 | 19.58 | 0.89 ± 0.62 | 3.35 | 0.52 |
| 10.14.2016 | 27.80 ± 9.33 | 46.17 | 13.74 | 0.36 ± 0.21 | 0.90 | 0.19 |
| Total | 38.93 ± 27.10 | 243.14 | 11.85 | 29.15 ± 91.50 | 1014.35 | 0 |
| Parameter | Range | Earlier Published | Unit | Reference | |
|---|---|---|---|---|---|
| Semi-analytical algorithm for Chl-a | 560–720 | 560 | nm | [37] | |
| 0.1–6.0 | 2.0 | - | [38] | ||
| 0.1–4.0 | 1.0 | - | |||
| −3.0–−0.1 | −1.2 | - | |||
| −1.0–−0.1 | −0.9 | - | |||
| 400–500 | 443 | nm | |||
| Semi-analytical algorithm for PC | 400–500 | 412 | nm | [14] | |
| 501–600 | 510 | nm | |||
| 1–100 | 98 | - | |||
| 0.18–3.0 | 0.2092–1.5053 | - | |||
| 0.001–0.3 | 0.0128–0.1911 | - | |||
| Independent backscattering | 1.0–2.0 | 1.61 | - | [18] | |
| −1–0 | −0.6 | - | |||
| Gons algorithm | 660–670 | 665 | nm | [29] | |
| 0.01–0.1 | 0.0161 | m2 mg−1 | |||
| Gilerson algorithm | 0.01–0.1 | 0.022 | m2 mg−1 | [6] | |
| 1.0–1.5 | 1.124 | - | |||
| Ritchie algorithm | −0.1–−1.0 | −0.3319 | - | [11] | |
| −0.1–−2.0 | −1.7485 | - | |||
| 5.0–15.0 | 11.9442 | - | |||
| −0.1–−2 | −1.4306 | - | |||
| 1.0–5.0 | 4.34 | - | |||
| Li algorithm | 615–625 | 620 | nm | [14] | |
| 0.001–0.01 | 0.007 | m2 mg−1 | |||
| Duan algorithm | 0–2 | 1.062 | - | [5] | |
| 0.01–0.1 | 0.0161 | m2 mg−1 | |||
| Simis algorithm | 0.1–1.0 | 0.68 | - | [12] | |
| 0.01–0.1 | 0.0343 | m2 mg−1 | |||
| Simis algorithm (PC) | 0.1–1.0 | 0.84 | - | [13] | |
| 0.1–1.0 | 0.24 | - | |||
| 0.001–0.01 | 0.007 | m2 mg−1 |
| Parameter | Gons | Gilerson | Ritchie | Simis | Duan | Li | Simis (PC) |
|---|---|---|---|---|---|---|---|
| 621 | 619 | 621 | - | - | 607 | - | |
| 5.7485 | 5.5645 | 5.3307 | - | - | 4.254 | - | |
| 3.7946 | 3.7535 | 3.8360 | - | - | 2.9641 | - | |
| −2.8742 | −2.5966 | −2.5106 | - | - | −1.338 | - | |
| −0.7709 | −0.7944 | −0.7965 | - | - | −0.6418 | - | |
| 478 | 472 | 466 | - | - | 474 | - | |
| - | - | - | - | - | 455 | - | |
| - | - | - | - | - | 531 | - | |
| - | - | - | - | - | 81 | - | |
| - | - | - | - | - | 1.9393 | - | |
| - | - | - | - | - | 0.4214 | - | |
| - | - | - | - | - | 0.2281 | - | |
| - | - | - | - | - | 0.1926 | - | |
| - | - | - | - | - | 0.0947 | - | |
| - | - | - | - | - | 0.0108 | - | |
| - | - | - | 1.9999 | 1.7982 | - | 1.9920 | |
| - | - | - | −0.9964 | −0.8489 | - | −0.9945 | |
| 660 | 660 | 660 | 660 | 660 | - | 662 | |
| 0.0750 | - | - | - | - | - | - | |
| - | 0.0777 | - | - | - | - | - | |
| - | 1.0017 | - | - | - | - | - | |
| - | - | −0.1305 | - | - | - | - | |
| - | - | −0.3534 | - | - | - | - | |
| - | - | 10.7271 | - | - | - | - | |
| - | - | −0.2612 | - | - | - | - | |
| - | - | 1.271 | - | - | - | - | |
| - | - | - | - | - | 615 | 615 | |
| - | - | - | - | - | 0.00941 | - | |
| - | - | - | - | 2.000 | - | - | |
| - | - | - | - | 0.0158 | - | - | |
| - | - | - | 0.1802 | - | - | 0.1669 | |
| - | - | - | 0.0742 | - | - | - | |
| - | - | - | - | - | - | 0.1547 | |
| - | - | - | - | - | - | 0.9559 | |
| - | - | - | - | - | - | 0.00305 |
| Single-Objective | Multi-Objective | |||
|---|---|---|---|---|
| Absorption Coefficient | Concentration Estimation | Absorption Coefficient | Concentration Estimation | |
| p * | p | p | p | |
| Gons | 3.352 × 10−19 | 1.000 × 10−4 | 5.247 × 10−10 | 0.058 |
| Gilerosn | 2.989 × 10−19 | 0.001 | 1.212 × 10−9 | 0.051 |
| Ritchie | 6.473 × 10−16 | 0.005 | 1.139 × 10−9 | 0.043 |
| Simis | 2.118 × 10−22 | 5.735 × 10−14 | 1.806 × 10−21 | 5.878 × 10−14 |
| Duan | 2.391 × 10−16 | 4.282 × 10−14 | 1.189 × 10−20 | 4.868 × 10−14 |
| Li | 1.815 × 10−15 | 0.020 | 4.409 × 10−9 | 3.914 × 10−12 |
| Simis (PC) | 3.342 × 10−19 | 1.015 × 10−7 | 5.200 × 10−16 | 1.774 × 10−8 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pyo, J.; Pachepsky, Y.; Baek, S.-S.; Kwon, Y.; Kim, M.; Lee, H.; Park, S.; Cha, Y.; Ha, R.; Nam, G.; et al. Optimizing Semi-Analytical Algorithms for Estimating Chlorophyll-a and Phycocyanin Concentrations in Inland Waters in Korea. Remote Sens. 2017, 9, 542. https://doi.org/10.3390/rs9060542
Pyo J, Pachepsky Y, Baek S-S, Kwon Y, Kim M, Lee H, Park S, Cha Y, Ha R, Nam G, et al. Optimizing Semi-Analytical Algorithms for Estimating Chlorophyll-a and Phycocyanin Concentrations in Inland Waters in Korea. Remote Sensing. 2017; 9(6):542. https://doi.org/10.3390/rs9060542
Chicago/Turabian StylePyo, JongCheol, Yakov Pachepsky, Sang-Soo Baek, YongSeong Kwon, MinJeong Kim, Hyuk Lee, Sanghyun Park, YoonKyung Cha, Rim Ha, Gibeom Nam, and et al. 2017. "Optimizing Semi-Analytical Algorithms for Estimating Chlorophyll-a and Phycocyanin Concentrations in Inland Waters in Korea" Remote Sensing 9, no. 6: 542. https://doi.org/10.3390/rs9060542
APA StylePyo, J., Pachepsky, Y., Baek, S.-S., Kwon, Y., Kim, M., Lee, H., Park, S., Cha, Y., Ha, R., Nam, G., Park, Y., & Cho, K. H. (2017). Optimizing Semi-Analytical Algorithms for Estimating Chlorophyll-a and Phycocyanin Concentrations in Inland Waters in Korea. Remote Sensing, 9(6), 542. https://doi.org/10.3390/rs9060542