1. Introduction
Semantic segmentation in remote sensing aims at accurately labeling each pixel in an aerial image by assigning it to a specific class, such as vegetation, buildings, vehicles or roads. This is a very important task that facilitates a wide set of applications ranging from urban planning to change detection and automated-map making [
1]. Semantic segmentation has received much attention for many years, and yet, it remains a difficult problem. One of the major challenges is given by the ever-increasing spatial and spectral resolution of remote sensing images. High spatial resolutions bring the great benefit of being able to capture a large amount of narrow objects and fine details in remote sensing imagery. However, increasing spatial resolutions incurs semantic segmentation ambiguities due to the presence of many small objects within one image and brings along a high imbalance of class distribution, huge intra-class variance and small inter-class differences. For example, a road in the shadows of buildings is similar to buildings with dark roofs, whereas the colors of cars may vary widely, which could cause confusions for the semantic classifiers. High spectral resolutions provide abundant information for Earth observations, but selecting, fusing and classifying hyperspectral images remain significant research challenges in remote sensing [
2,
3].
Semantic segmentation is often viewed in a supervised learning setting. Like many other supervised learning problems, the general approach for supervised semantic segmentation consists of four main steps: (i) feature extraction; (ii) model design and training; (iii) inference; and (iv) post-processing. In this paper, we focus on the semantic segmentation of high-resolution aerial images and propose a CNN-based solution by following this generic design methodology for supervised-learning.
In the literature, supervised methods have focused much on the feature extraction step and proposed to use a variety of hand-crafted descriptors. Classical methods focus on extracting spatial or spectral features using low-level descriptors, such as GIST [
4], ACC [
5] or BIC [
6]. These descriptors capture both the global color and texture features. In hyperspectral imagery, salient band selection can help feature extraction by reducing the high spectral-resolution redundancy. Lately, mid-level descriptors have became more and more popular in computer vision. One of the most successful descriptors is the bag-of-visual-words (BoVW) descriptor [
7,
8]. Thanks to its effectiveness, the BoVW descriptor has been widely used in remote sensing in scene recognition and semantic labeling. Sub-space learning techniques were proposed to automatically determine the feature representation of a given dataset by optimizing the feature space [
9,
10,
11]. By making use of a broad variety of descriptors, an image can be represented by many different features. Each feature has its own advantages and drawbacks; hence, selecting the best features for a specific type of data is particularly important. To achieve this goal, several feature selection frameworks were proposed, such as that of Tokarczyk et al. [
12], who designed a boosting-based method to select optimal features in the training process from a vast randomized quasi-exhaustive (RQE) set of feature candidates.
In recent years, the focus was put on feature learning and using learned features for semantic segmentation. Cheriyadat [
13] proposed to use sparse coding to guide feature learning. In [
14], an improved object detection performance is reached by using a spatial sparse coding bag-of-words model. Recently, the rapid development in deep learning, especially in convolutional neural networks, has brought unified solutions for both feature learning and semantic classification of remote sensing images. Having started as a breakthrough in image classification [
15], CNNs have proven to be able to significantly improve state-of-the-art performance in numerous computer vision domains [
16]. For example, CNNs with a ResNetarchitecture [
17] have won the ILSVRC2015 competition with an error rate of 3.6%, which even surpasses human performance for image classification. For pixel-wise vision tasks like semantic segmentation, CNNs also outperform classical methods [
18,
19]. In remote sensing, more and more research has been focused on designing and applying CNNs for semantic segmentation. Paisitkriangkrai et al. applied both patch-based CNNs and hand-crafted features to predict the label of each pixel [
20]. In addition, conditional random field (CRF) processing follows prediction to provide a smooth final result. Kampffmeyer et al. applied a fully-convolutional network structure to solve pixel-wise labeling of high resolution aerial images in an end-to-end fashion [
21]. A weighted loss function was used in their network to address the class imbalance problem. Volpi et al. proposed to apply several learnable transpose convolutional layers to up-sample the scores to the input size, trying to avoid the possible spatial information loss during the up-sampling stage [
22]. Nevertheless, existing methods in the literature, especially deep learning-based methods, suffer from two major problems, namely the insufficient spatial information in the inference phase and the lack of contextual information. These problems result in poor segmentations around object boundaries, as well as in other difficult areas, such as shadow regions.
To overcome these problems, in this paper, we introduce a novel hourglass-shaped network architecture for pixel-wise semantic labeling of high-resolution aerial images. Our network is structured into two parts. These parts, namely encoding and decoding, perform down-sampling and up-sampling respectively to infer class maps from input images. Compared to existing designs, our novel contributions are as follows:
We leverage skip connections with residual units and an inception module in a generic CNN encoder-decoder architecture to improve semantic segmentation of remote sensing data. This combination benefits multi-scale inference and forwards spatial and contextual information directly to the decoding stage.
We propose to apply overlapped inference in semantic segmentation, which systematically improves classification performance.
We propose a weighted belief-propagation post-processing module, which addresses the border effects and smooths the results. This module improves the visual quality, as well as the classification results on segment boundaries.
Extensive experiments on two well-known high resolution remote sensing datasets demonstrate the effectiveness of our proposed architecture compared to state-of-the-art network designs.
The remainder of the paper is organized as follows. A brief review of convolutional neural networks is given in
Section 2, followed by an analysis of existing architectures for semantic segmentation in remote sensing.
Section 3 presents our proposed hourglass-shaped network architecture and details the training and inference methods. Experimental settings and results are presented in
Section 4.
Section 5 discusses the proposed approach and experimental results, while
Section 6 concludes our work.
2. Convolutional Neural Networks
Convolutional neural networks [
15] stem from conventional neural network designs. CNNs consist of layers of neurons, where each neuron has learnable weights and biases. The whole network serves as a complex non-linear function, which transforms the inputs into target variables. The difference with respect to conventional networks is that CNNs comprise specific types of layers and composing elements dedicated to perform specific functions, such as computing convolution, down-sampling or up-sampling operations.
In this section, we first present a short overview of the common layer types employed in CNN architectures. This is subsequently followed by a summary of existing CNN architectures for semantic segmentation.
2.1. Composition Elements
In this section, we present the four basic types of layers that are used in CNNs for semantic segmentation: the convolutional layer, transposed convolutional layer, non-linear function layer and the spatial pooling layer. These are detailed next.
2.1.1. Convolutional Layer
The convolutional layer is the core of CNNs. It can be seen as a bank of simple filters with learnable parameters. As illustrated in
Figure 1a, the layer takes the input
X of size
and convolves it with the filter bank by sliding of stride
S and padding the border with
P units. The result of this operation is an output volume
Y with size
. Equation (
1) formulates the calculation of the output at spatial position
as:
where
are the learnable parameters (weights and bias) of the layer,
is the corresponding receptive field (or a window surrounding
) and
denotes the dot product between
W and
N.
The spatial dimensions of the output of the convolutional layer are given by , where F is the size of the receptive field, which also corresponds to the spatial size of the filters. In general, each filter can take different widths and heights, but conventionally, most CNN architectures employ filters with square masks of dimension F. In our work, we consider only filters with square masks.
Neurons in the output volume Y can be considered as filters of size . Intuitively, each neuron looks for a specific pattern in the input volume X. Since we want to look for the same pattern across all spatial locations in the input volume, the learnable weights and bias for all neurons in a channel of Y are shared. This is often called parameter sharing, and by doing this, the output volume Y consists of the values obtained when applying filters on the input volume X. The parameter sharing also reduces the number of weights of a convolutional layer to , which is much smaller than that of a fully-connected layer. This helps mitigate the problem of overfitting in neural network training.
2.1.2. Transposed Convolutional Layer
The transposed convolutional layer, also known as the deconvolution layer, was first introduced in [
23]. An example of the transposed convolutional layer is shown in
Figure 1b. This layer is commonly employed for up-sampling operations in CNNs [
18]. As shown in
Figure 1b, the input is first up-sampled by a factor of stride
S and padded spatially with
P units if necessary. After that, convolution is applied to the up-sampled input with a filter bank that has a receptive field of size
F. Transposed convolution can be thought of as the inverse operation of convolution. Filter parameters can be set to follow conventional bilinear interpolation [
18] or can be set to be learned.
2.1.3. Non-Linear Function Layer
The convolution layer is often followed by a non-linear function layer, also called an activation function. The role of this layer is similar to that of a fully-connected layer in traditional neural networks. This layer introduces non-linearity in the network and enables the network to express a more complex function. Common activation functions include the Sigmoid function, the Tanh function, the rectified linear unit (ReLU) function [
24] and the leaky ReLU function [
25]. Among these functions, the ReLU function
is the most commonly used in deep-learning research. In our proposed network design, we also select ReLU as the activation function due to its efficiency and light computational complexity.
2.1.4. Spatial Pooling Layer
The spatial pooling layer is used to spatially reduce the size of the input volume [
26]. A small filter (typical size: 2 × 2 or 3 × 3) is used to slide through the volume to carry out a simple spatial pooling function. Common pooling functions include max, mean and sum functions. One notes that it is also possible to use the convolutional layer to replace the pooling layer [
27]. However, this practice does not necessarily lead to performance benefits and would cost extra memory and training effort [
28]. Among the common pooling functions, the max function is most commonly used in the literature. We also employ the max pooling function in our network design.
2.2. CNN Architectures for Semantic Segmentation of Remote Sensing Images
In the literature, there are two basic approaches for semantic segmentation, namely patch-based and pixel-based approaches. In this section, we present an analysis of both categories.
2.2.1. Patch-Based Methods
Patch-based approaches infer the label of each pixel independently based on its small surrounding region. In these approaches, a classifier is designed and trained to predict a single label from a small image patch. In the inference phase, a sliding window is used to extract patches around all pixels in the input image, which are subsequently forwarded through the classifier to get the target labels [
29]. Several techniques have been proposed to achieve high performance with patch-based approaches. For instance, replacing the fully-connected layer in the network with convolutional layers can lead to more efficient algorithms by avoiding overlapping computations [
22,
29]. Multi-scale inference and recurrent refinements can also lead to performance gains [
30,
31]. Nevertheless, patch-based approaches are often outperformed by pixel-based methods in remote sensing semantic segmentation tasks [
21,
22]. As a result, in this work, we put more emphasis on the pixel-based approach and follow such a paradigm in our design.
2.2.2. Pixel-Based Methods
Unlike patch-based approaches, pixel-wise methods infer the labels for all of the pixels in the input image at the same time. One of the first CNN architectures for pixel-wise semantic segmentation is the fully-convolutional network (FCN) method introduced by Long et al. in [
18]. In this method, a transposed convolutional layer is employed to perform up-sampling. This operation is essential in order to produce outputs of the same spatial dimensions as the inputs.
The FCN architecture was recently employed for semantic segmentation of remote sensing images in [
21]. Its architecture, shown in
Figure 2, can be divided into two parts, namely encoding and decoding. The latter is depicted within the dotted-line box in the figure. The encoding part follows the same architecture as the VGG-net of [
32], which is one of the most powerful architectures for image classification. In
Figure 2, the layers A, B, C and D are convolutional layers; their configurations (width, height, depth) are shown in
Table 1. Each convolutional layer is followed by a batch normalization layer [
33] and ReLU activation function. The final convolutional layer of Type D is followed by a 1 × 1 convolution, producing an output with scores for each classes. Layer E is a max pooling layer with size
and stride
. It performs a down-sampling operation with a factor of two in each dimension. Layer F is a transposed convolutional layer, with filter size
and stride number
. It up-samples the scores to original image size. It should be noted that after each pooling layer, the number of filters in the next convolutional layers is doubled to compensate the spatial information loss. To train the network, a median frequency weighted softmax loss layer (Layer G) is appended after the last transposed convolutional layer.
In this FCN design [
21], the transposed convolutional layer up-samples the score by a large factor of eight in each dimension. This incurs the risk of introducing classification ambiguities in the up-sampled result. To mitigate this problem, in [
22], Volpi et al. proposed to use multiple transposed convolutional layers to progressively up-sample the classification scores. This design is named full patch labeling by learned up-sampling (FPL) [
22], its architecture being depicted in
Figure 2. Similar to FCN, the FPL network also consists of encoding and decoding modules. However, unlike the FCN design, which incorporate unique layer types in each convolutional module, in FPL, the convolutional modules consist of all four different convolutional layer types, A, B, C and D (see
Figure 2). Their configurations are shown in
Table 1. Each convolutional module is followed by a max pooling layer, batch normalization layer and leaky ReLU activation. In
Figure 2, the pooling and leaky ReLU layers in FPL are grouped together and shown as Layer E. In the decoding stage, three transposed convolutional layers (Type F) are stacked sequentially to spatially up-sample the score to the input image size. They all have an up-sampling factor of two in each spatial dimension. For training, a softmax loss layer (Type G) is appended at the end of the network. The FCL design aims at improving the output classification result by allowing the transpose convolutional layers to learn to recover the fine spatial details. Semantic segmentation results on the Vaihingen dataset reported in [
22] show that the FPL network outperforms the FCN design in terms of overall accuracy.
Besides using the transposed convolutional layer for up-sampling in the decoding stage, Vijay et al. proposed to use unpooling in SegNet [
19] for pixel-wise segmentation tasks. The encoder part of SegNet (see
Figure 2) consists of consecutive convolution layers with uniform 3 × 3 size filters, followed by ReLU activations and pooling layers. The detailed network parameter settings are given in
Table 1. The decoder uses pooling indices computed in the max-pooling step of the corresponding encoder to perform non-linear up-sampling (via an unpooling Layer F), followed by mirror-structured convolution layers to produce the pixel-wise full size label map. Finally, a loss Layer G is attached for network training. The SegNet design aims at preserving the essential spatial information by remembering the pooling indices in the encoding part, which produces state-of-the-art accuracy in generic image segmentation tasks.
Both FCN and FPL architectures suffer from two problems, namely the insufficient spatial information in the decoding stage and the lack of contextual information. Due to the first problem, the FCN and FPL networks often mislabel small objects like cars and produce poor results around object boundaries. Due to the second problem, the lack of contextual information makes it difficult for these architectures to correctly infer classes in difficult areas, such as shadow regions projected by high-altitude buildings and trees.
SegNet effectively mitigates the insufficient spatial information problem by adopting unpooling layers in the decoder part, but it may also suffer from the lack of contextual information. Furthermore, as shown in
Table 2, SegNet has three-times more trainable weights than FCN and FPL, making the training phase much more difficult. In this paper, we propose a novel network architecture to address these issues.
3. Proposed CNN Architecture for Semantic Segmentation
In this section, we present our novel CNN architecture for semantic segmentation of remote sensing images. The section details first the network design, followed by the training and inference strategies, our post-processing technique and a brief analysis.
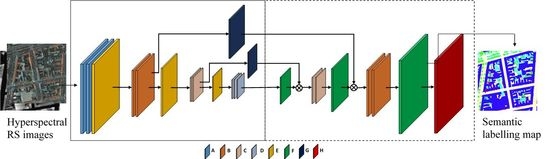
3.1. Proposed Hourglass-Shaped Convolutional Neural Network
Our CNN follows a pixel-wise design paradigm, which has been shown to produce state-of-the-art results in semantic segmentation. However, as mentioned in
Section 2.2, existing pixel-wise network architectures suffer from the spatial-information loss problem. To overcome this problem, we propose a novel hourglass-shaped network (HSN) architecture. Our HSN design was partially inspired from recent important works in deep learning research [
17,
34,
35].
3.1.1. Network Design
Similar to FCN and FPL, our HSN architecture follows the generic encoder-decoder paradigm, as illustrated in
Figure 3. In the figure, the encoder and decoder parts are delimited by continuous and dashed rectangular boxes, respectively. As mentioned in
Section 2.2, one key point is to use transposed convolutional layers to progressively up-sample the pixels’ class scores to the original spatial resolution of the input image. However, novel components are brought in the network design. Inspired by the hourglass-shaped network introduced for human pose estimation [
36] and image depth estimation [
35], we propose a network that features (i) multi-scale inference by using inception modules [
34] replacing simple convolutional layers and (ii) forwarding information from the encoding layers directly to decoding ones by skip connections.
The network starts with two layers of A and two layers of B, which are common convolutional layers with filter size
. The number of filters are 64 and 128 for Layers A and B, respectively. Each convolution layer is followed by a batch normalization layer and ReLU activation. Layer E is a max pooling layer, with a down-sampling factor of two. Layers C and D are composed of inception modules, as shown in
Figure 4a. The configurations of convolutional layers in the inception modules are shown in
Table 3. As can be seen from the table, filters of different sizes are assembled in one inception module to enable multi-scale inference through the network.
In the encoding part, after the second Layer B and after Layer C, two skip branches are made with Layer G, forwarding information directly to the corresponding layers in the decoding part. Layer G is a residual module inspired by ResNet [
17]. The residual module is shown in
Figure 4b, where
is a bank of 128 filters with size 1 × 1, and
is another bank of 128 filters with size
. The input of the module is directly element-wise added to the output of
. It is worth mentioning that, due to the use of filters with size 1 × 1, the number of trainable weights for the whole network is significantly reduced. As shown in
Table 2, the total number of trainable weights of HSN is comparable to that of FPL and nearly three-times less than that of SegNet.
In the decoding part, Layer F serves as the transposed convolutional layer, with the same up-sampling factor of two. After the first and second up-sampling, data directly forwarded from the encoding part are concatenated with the outputs of the transposed convolutional layers. Finally, Layer H, which is a weighted softmax layer, is used in the training phase of the network.
3.1.2. Median Frequency Balancing
We train our network using the cross-entropy loss function, which is summed over all of the pixels. Nevertheless, the ordinary cross-entropy loss can be heavily affected by the imbalance of the class distribution when applied to high-resolution remote sensing data. To address this problem, the loss for each pixel is weighted based on the median frequency balancing [
21,
37] technique. The weighted loss for a pixel
i is calculated as:
where
is the ground-truth class of pixel
i,
is the weight for class
c,
is the pixel frequency of the class and:
3.2. Training Strategy
We train the network to optimize the weighted cross-entropy loss function using mini-batch stochastic gradient descent (SGD) with momentum [
38]. The parameters are initialized following [
39]. The learning rate is set to step down 10-times from
every 50 epochs, with momentum set to 0.99. The batch size is set to fit the memory. Data augmentation is carried out to mitigate overfitting. The image patches are extracted with size
with 50% of overlap and flipped horizontally and vertically. Each patch is also rotated at 90 degree intervals. In total, this produces eight augmentations for each overlapping patch. We train our network from scratch until the loss converges. Batch normalization is employed, similar to existing network architectures. The training and testing processes are performed on a desktop machine equipped with Nvidia GeForce Titan X (12 Gb vRAM).
3.3. Overlap Inference
In the inference stage, due to the memory limit, the input high-resolution images can be sliced into small non-overlapping patches to feed-in the network. However, this may cause inconsistent segmentation across the patch borders and hence result in degraded accuracy.
To address such boundary effects, overlap inference is employed whereby input images are split into overlapped patches. At the output of the network, the class scores in overlapped areas are averaged. We experimentally justify the benefit of this strategy compared to non-overlapping inference in
Section 4.
3.4. Post-Processing with Weighted Belief Propagation
Semantic segmentation for high-resolution remote sensing imagery often requires accurate and visually clear results to serve further automatic processing or manual investigations. However, the raw network output may feature zigzag segment borders and incorrect blobs. Some examples are shown in
Figure 5,
Figure 6 and
Figure 7. To address this problem, we propose to use weighted belief propagation for post-processing the raw network outputs.
In the proposed HSN architecture, the semantic label for a pixel at an arbitrary position i is determined as , where denotes the score of class c for pixel i. This corresponds to the top one class prediction, i.e., the class label with the highest score. Similarly, the top two prediction for any arbitrary pixel is defined as the set of class labels when taking the best two scores for that pixel. We experimentally observed that the top two prediction accuracy for the validation data is around 97% on the Vaihingen dataset. This shows that most of the time, the right labels lie in the top two scores determined by the network.
Let , in which and refer to the top two scores, i.e., the highest and second highest class scores for pixel i, respectively. Intuitively, for a trained network, the higher is, the more confident the network is about its prediction. Therefore, can be thought of as the confidence of the output at position i.
We consider post-processing as a pixel labeling problem and formulate a Markov random field (MRF) model to solve it. A node
i in our MRF model corresponds to a pixel in the original image
I, which is directly connected to its four spatial neighbors
.
denotes the class label assigned to node
i. We find the optimal labels for the whole image by minimizing the following energy function:
where
, defined in Equation (
5), refers to the data energy term describing how confident the estimated label
is;
is the smoothness energy defined in Equation (
6), which penalizes the inconsistency between node
i and its neighbors
:
where
and
T are hyper-parameters, which are set empirically, and
is the Dirac delta function. We employ the weighted belief propagation algorithm (WBP) [
40,
41] to iteratively minimize the energy function
E. At each iteration, the update rule of WBP is expressed by Equations (
7) and (
8) below:
in which
is the message passed from node
i to node
j;
is the weight for node
i, which is set to its confidence value
;
is the belief, which represent how confident the node
i is to take label
.
The messages are updated until convergence. The final label at node i is determined by .
5. Discussion
The experimental results in
Section 4 prove that state-of-the-art performance on well-known remote sensing datasets is achieved with our approach. On the Vaihingen dataset, the proposed approach outperforms reference methods by substantial margins in terms of both average F-score and overall accuracy. On the Potsdam dataset, it is marginally worse than SegNet in term of average F-score, but noticeably better in terms of overall accuracy. Besides, the proposed approach systematically performs better than FCN and FPL on this dataset. In addition, this high performance is achieved with relatively low complexity. The number of trainable parameters in our network is just slightly higher than that of FPL while being far lower than those of FCN and especially SegNet, which has three-times more parameters than the proposed network.
We argue that the effectiveness of the propose approach comes from the highly complementary characteristics of different components in the architecture. Firstly, the use of skip connection with residual modules helps with transferring spatial information from the encoder directly to the decoder, improving the segmentation around object borders. Secondly, the use of inception provides the decoder with richer contextual information. This helps the network to label difficult areas such as roads, which are shadowed and which can be correctly inferred if enough surrounding contexts are available. Richer spatial and contextual information in the decoder also resolves the class ambiguities, especially in high resolution images. Thirdly, the weight balancing employed during training mitigates the class imbalance problem and improves the labeling of classes that account for a small number of pixels, e.g., the car class. This is of particular significance when working with remote sensing data of high resolutions. Fourthly, overlapped inference, which returns the final segmentation making use of multi-hypothesis prediction, diminishes the patch border effects and improves the robustness of the results. Finally, post-processing based on weighted belief propagation corrects the object borders and erroneous small blobs and systematically improves the segmentation results both quantitatively and visually. Combining all of these components, especially the skip connections and inception module in the CNN, mitigates the two problems of existing approaches in the literature, namely insufficient spatial information and lack of contextual information.
Possible directions for future research include: reducing the memory consumption while keeping efficiency and enough spatial and contextual information for high quality segmentation; improving the generalizability of the network by employing more data augmentation. This will be highly relevant in some applications in which large datasets are impossible or expensive to obtain.
6. Conclusions
In this paper, we propose a novel hourglass-shape network architecture for semantic segmentation of high-resolution aerial remote sensing images. Our architecture adopts the generic encoder-decoder paradigm and integrates two powerful modules in state-of-the-art CNNs, namely the inception and residual modules. The former assembles differently-sized filters into one layer, allowing the network to extract information from multi-scale receptive areas. The latter is employed together with the skip connection, feeding forward information from the encoder directly to the decoder, making use more effectively of the spatial information. Furthermore, our solution for remote sensing semantic segmentation employs (i) weighted cross-entropy loss to address the class imbalance problem in the training phase, (ii) overlap processing in inference phase and (iii) weighted belief propagation for post-processing.
Extensive experiments on well-known high-resolution remote sensing datasets demonstrate the effectiveness of our proposed approach. Our hourglass-shaped network outperforms state-of-the-art networks on these datasets in terms of overall accuracy and average F-score while being relatively simpler in terms of the number of trainable parameters.